Sorting - Insertion / Selection / Shell Sort

Total Order

Total Order란 대소 관계를 정의할 때 반드시 지켜야 하는 규칙을 의미한다.
규칙은 다음 세가지로 이루어진다.

Total order의 규칙

• Antisymmetry : a <= b 이고 b <= a 라면, a == b 여야 한다.
• Transitivity : a <= b 이고 b <=c 라면, a <=c 이다.
• Totality : a < b 이거나 a > b 이거나 a == b 이다.

숫자나 알파벳의 경우, 일일이 따져보지 않아도 세 규칙이 모두 성립한다는 것을 알 수 있다.
그래서 우리는 숫자와 알파벳을 정렬할 수 있는 것이다. 두 원소간에 대소 관계가 명확하므로.

Total Order를 어기는 경우 - 가위바위보

그럼 Total Order를 어기는 경우를 생각해보자. 가위바위보는 어떨까?

가위바위보의 대소 관계

• 가위 > 보 : 가위는 보자기를 이긴다.
• 보 > 바위 : 보는 바위를 이긴다.
• 바위 > 가위 : 바위는 가위를 이긴다.

가위바위보는 Total Order 중에서도, Transitivity를 충족하지 않는다.
'가위 > 보'이고 '보 > 바위' 이면 Transitivity에 의해 '가위 > 바위'여야 하지만, 실제로는 그렇지 않다.

Total order와 Sorting

Antisymmetry, Transitivity, Totality 세가지 규칙을 모두 지키는 경우, Total Order를 만족한다고 하며 정렬 알고리즘을 사용했을 때 올바른 결과를 얻을 수 있다.

---

Selection Sort

Selection Sort는 매 iteration마다 입력 데이터의 일부 중에서 가장 작은 원소를 선정해(selection) 앞으로 이동시키는 방식이다.
동작 방식을 간략히 알아보자.

Selection Sort 동작

초기화 : arr = [2, 3, 4, 1]

• iteration 0 결과 : [1, 3, 4, 2]
  • i번째 원소(2) ↔ 최솟값 원소(1)
• iteration 1 결과 : [1, 2, 4, 3]
  • i번째 원소(3) ↔ 최솟값 원소(2)
• iteration 2 결과 : [1, 2, 3, 4]
  • i번째 원소(4) ↔ 최솟값 원소(3)
• iteration 3 결과 : [1, 2, 3, 4]
  • i번째 원소(4) ↔ 최솟값 원소(4)

Iteration i 때 arr[i] ~ arr[N-1] 중 최솟값을 찾아 arr[i]와 swap하며 정렬해나간다.

코드

def selection_sort(arr):
  for i in range(len(arr)-1):  #1
      minIdx = i  
      for j in range(i+1, len(arr)):  #2
          if arr[minIdx] > arr[j]:
              minIdx = j
      arr[i], arr[minIdx] = arr[minIdx], arr[i]  #3

1. i = 0~N-2의 iteration에 대해 진행한다.
2. 각 iteration에서 arr[i]~arr[N-1] 중 최솟값을 찾는다.
3. i번째 원소와 최솟값 원소를 swap한다.

성능

매 iteration(0~N-2)마다 i~N-1 구간을 순회하며 대소 비교를 진행하므로, O(N^2)의 시간 복잡도를 가진다.
Selection Sort의 경우 반드시 위에서 언급한 구간을 몽땅 순회하기 때문에 거의 정렬된 상태의 데이터를 정렬하는 상황에서 비효율적으로 동작한다.

---

Insertion Sort

Selection Sort는 매 iteration마다 정렬된 상태인 arr[0] ~ arr[i-1]에 새로운 한 원소 arr[i]를 적절한 위치에 추가하는(insert) 방식이다.

동작 방식을 간략히 알아보자.

Selection Sort 동작

초기화 : arr = [4, 1, 3, 2]

• iteration 0 결과 : [4, 1, 3, 2]
  • 4의 왼쪽에 원소가 없으므로 stop
• iteration 1 결과 : [1, 4, 3, 2]
  • 4 > 1 이므로 4와 1을 swap
• iteration 2 결과 : [1, 3, 4, 2]
  • 4 > 3 이므로 4와 3을 swap
  • 1 < 3 이므로 stop
• iteration 3 결과 : [1, 2, 3, 4]
  • 4 > 2 이므로 4와 2를 swap
  • 3 > 2 이므로 3과 2를 swap
  • 1 < 2 이므로 stop

iteration i에 arr[i]를 왼쪽에 그보다 작거나 같은 원소가 나오기 직전까지 swap하며 정렬해나간다.

예시

코드

def selection_sort(arr):
    for i in range(1, len(arr)):  #1
        key = arr[i]  
        j = i - 1
        while j >= 0 and arr[j] > key:  #2
            arr[j + 1] = arr[j]
            j -= 1

    arr[j + 1] = key  #3

1. arr[1]~arr[N-1]까지 iteration (arr[0]은 이미 정렬된 상태이므로 제외)
2. a[j] > key이면 a[j]를 오른쪽으로 한 칸 이동시킨다.
3. a[j] <= key이거나, j가 -1이 되면 while문을 탈출하며 arr[j+1]이 arr[i]의 위치가 된다.

성능

입력 데이터가 이미 정렬된 상태로 들어온다면, 매 iteration에서 원소의 이동이 발생하지 않는다.
~N의 비교만 발생한다.

최악의 경우, 매 iteration마다 a[i] 왼쪽의 원소 i-1개와 비교를 하고, 같은 수의 swap을 해야하므로 n-2)(n-1)/2 회의 비교와 swap이 이루어진다. 따라서 시간복잡도는 O(N^2)이다.

입력이 거의 정렬 되어서 들어오는 경우가 많다면(partially ordered) N에 비례한 횟수의
비교/swap만 수행하므로 Selection Sort가 다른 정렬 방법보다 유리하다고 할 수 있다.

---

Shell Sort

Inversion

inversion이란 정렬 순서가 어긋난 쌍을 의미한다.

[A, E, E, L, M, O, T, R, X, P, S] 의 inversion 수

• 총 6개가 존재한다.
  • T-R
  • T-P
  • T-S
  • R-P
  • X-P
  • X-S

Insertion Sort는 inversion의 수만큼 swap을 수행한다.

만약 inversion이 없다면 이미 정렬된 상태를 의미한다. Insertion Sort는 왼쪽에 그보다 작거나 같은 원소가 나오기 직전까지 한번에 한 원소씩 왼쪽으로 이동해나간다.
이는 한번 이동(swap)할 때마다 하나의 inversion이 해결됨을 의미한다. 대소 관계가 어긋난 쌍을 swap하기 때문이다.

inversion 관점에서 본 insertion sort의 성능

insertion sort는 inversion의 수에 따라 그 성능이 달라진다.

앞에서 말했듯 이미 정렬된 상태여서 inversion의 수가 0인 경우, 해결할 inversion이 없기 때문에 swap 또한 이뤄지지 않는다.

만약 정렬 순서와 반대로 정렬된 '최악의' 상황이라면 i번째 원소는 그 이전 원소와 모두 inversion이 생긴다.
따라서 총 1 + 2 + ... + N-1 = (N-1)(N-2)/2 개의 inversion이 발생한다.

h-sort

Inversion Sort가 한번의 swap으로 하나의 inversion을 해결하는 것과 달리, Shell Sort는 한번의 swap으로 여러개의 inversion을 해결한다.

h-sort는 h만큼 떨어진 원소끼리 insertion sort 방식을 이용해 정렬하는 것을 의미한다.

4-sort를 수행한 예

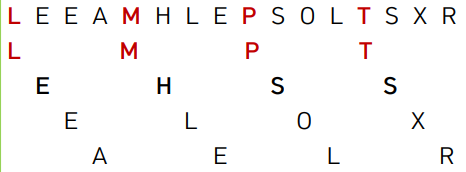
3-sort를 수행한 예

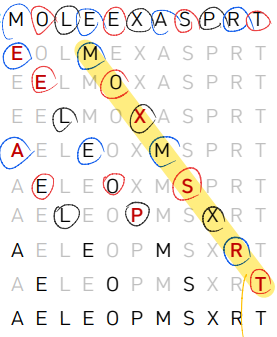
1-sort를 수행한 결과는 기존의 insertion sort를 수행한 결과와 동일하다.
h가 클수록, 정렬이 완벽에 가까워지기 때문에 swap이 더 많이 발생한다.

h-sort의 코드는 다음과 같다.

h-sort 코드

def h_sort(arr, h):
    for i in range(h, len(arr)):  #1
        key = arr[i]  
        j = i - h
        while j >= 0 and arr[j] > key:  #2
            arr[j + h] = arr[j]
            j -= h

    arr[j + h] = key  #3

이는 insertion sort에서의 1을 모두 h로 수정한 것과 동일하다.

insertion sort 코드

def selection_sort(arr):
    for i in range(1, len(arr)):  #1
        key = arr[i]  
        j = i - 1
        while j >= 0 and arr[j] > key:  #2
            arr[j + 1] = arr[j]
            j -= 1

    arr[j + 1] = key  #3

Shell Sort

Shell Sort는 h를 점진적으로 1까지 감소시켜 가며 h-sort를 수행하는 정렬 방법이다.
왜 이렇게 할까? h-sort는 한번의 swap으로 여러 개의 inversion을 해결한다.
h-sort는 여러 칸 앞으로 가야할 원소를 한번에 h칸씩 앞으로 이동시킨다. 즉, 하나의 swap으로 여러 개의 inversion을 해결한다.

따라서, h를 줄이면서 h-sort를 반복하면 적은 수의 swap으로 점차 완벽하게 정렬할 수 있다.

예시

이때 h는 1씩 감소시키지 않고, 그보다 큰 간격으로 감소시킨다.

어떤 h값을 사용하는 것이 최적인지는 아직 연구가 이루어지고 있다. 현재로서는 3x+1로 h를 계산하는 것이 다음 h를 계산하기 쉬울 뿐더러 성능도 준수하여 많이 사용된다.

h값 선택 : 3x+1

하지만 어떻게 h값을 정해서 사용하든지, 최종적으로는 1-sort를 수행해 완전히 정렬된 상태로 만들어야 한다.
h가 1보다 큰 h-sort에서 '완벽'은 확률적 개념에 가깝기 때문이다.

코드

def h_sort(a, h):
    numSwaps = 0  
    for i in range(h, len(a)):  
        key = a[i]     
        j = i-h
        while j>=0 and a[j] > key:
            a[j+h] = a[j] 
            numSwaps += 1
            j -= h         
        a[j+h] = key   
    return a, numSwaps


def shellSort(a):
    N = len(a)
    h = 1
    while h < N / 3:
        h = 3 * h + 1  

    numSwapsTotal = 0
    while h >= 1:
        _, numSwaps = h_sort(a, h)
        numSwapsTotal += numSwaps
        h = h // 3

    return a, numSwapsTotal

성능

shell sort의 경우, 아직 정확한 수학적 모델을 찾지는 못했지만, h=3x+1을 사용하는 경우에 ~(logN)회의 h-sort를 수행한다. 따라서 O(NlogN)의 성능을 가질 것으로 예측되고 있다.