일반적으로 알려져있고 잘 사용되는 해시 함수의 종류에 대해 알아본다.
1. 해시 함수란?
해시 함수는 데이터를 고정된 크기의 숫자 값으로 변환하는 함수이다. 결과로서 나온 숫자 값이 해시 테이블의 인덱스로 사용된다.
2. 일반적인 해시 함수
2-1. Division Method
키를 배열 크기로 나눈 나머지를 해시 값으로 사용한다. 이때 키가 숫자가 아닌 경우 문자열이나 다른 데이터 타입의 키를 숫자로 변환하는 전처리 단계를 거친다. 예를 들어, 문자열 키를 숫자로 변환하는 간단한 방법은 문자열의 각 문자에 대한 ASCII 코드나 Unicode 코드 값을 합하는 것이다. 이렇게 합산된 값은 Division Method를 사용하여 해시 값을 생성하는 데 사용될 수 있다.
2-2. Multiplication Method
키에 일정한 값을 곱한 후, 결과의 소수점 부분에 해시 테이블의 크기를 곱하여 해시 값을 얻는 방법이다. 마찬가지로 키가 숫자가 아닌 경우 키를 숫자로 변환하는 전처리 과정을 거친다.
2-3. Universal Hashing
Universal Hashing은 충돌의 확률을 최소화하기 위해 무작위로 선택된 해시 함수 집합 중에서 하나의 해시 함수를 사용하는 방법이다.
Universal Hashing의 기본적인 동작 과정은 다음과 같다.
- 가능한 여러 해시 함수들의 집합을 정의한다.
- 이 집합에서 무작위로 하나의 해시 함수를 선택하여 사용한다.
- 만약 충돌이 발생하면, 다른 해시 함수를 선택하여 사용할 수도 있다. 그러나 일반적으로는 초기에 선택된 해시 함수를 계속 사용하며, 다른 방법(예: 체이닝)으로 충돌을 해결한다.
Universal Hashing의 주요 장점은 어떤 특정한 키 집합에 대해서도 평균적으로 균등한 분포를 가지는 해시 값을 생성한다는 것이다. 이는 악의적인 공격이나 특정 패턴의 키 집합이 주어졌을 때 해시 테이블의 성능을 안정적으로 유지할 수 있게 해준다.
3. 암호화 해시 함수
암호화 해시 함수는 데이터의 무결성과 인증을 보장하기 위해 설계된 특별한 종류의 해시 함수이다. 주어진 입력에 대해 고정된 길이의 출력 값을 생성하며, 작은 입력의 변화도 출력에 큰 변화를 일으키는 특징이 있다. Merkle–Damgård와 Miyaguchi-Preneel 구조라는 말이 나오는데 목록 4에서 설명한다.
3-1. MD5 (Message Digest Algorithm 5)
MD5는 Merkle–Damgård 구조를 기반으로 한다. 입력 데이터를 512비트 블록으로 나눈 후 각 블록을 처리하여 최종적으로 128비트 해시 값을 생성한다. 빠른 연산 속도를 가지지만, 충돌 취약성이 발견되어 현재는 보안 목적으로 사용되지는 않는다고 한다.
3-2. SHA (Secure Hash Algorithm)
SHA도 MD5와 같이 Merkle–Damgård 구조를 사용한다. SHA-1은 160비트 해시 값을 생성하며, SHA-256은 256비트, SHA-512는 512비트 해시 값을 생성합니다. SHA-1은 MD5와 유사한 보안 취약점이 발견되어 권장되지 않는다. SHA-256 이상의 버전은 현재 널리 사용되며, 보안성이 높다.
3-3. Whirlpool
Whirlpool은 Merkle–Damgård 구조를 확장한 Miyaguchi-Preneel 구조를 사용한다. 입력 데이터를 512비트 블록으로 나눈 후, 각 블록을 처리하여 512비트 해시 값을 생성한다. Whirlpool 또한 보안성이 높다.
4. Merkle–Damgård 구조와 Miyaguchi-Preneel 구조
이 두 구조를 자세히 알기 위해서는 암호학적으로 알아야 할 지식이 있기 때문에 간단히만 설명한다.
4-1. Merkle–Damgård 구조
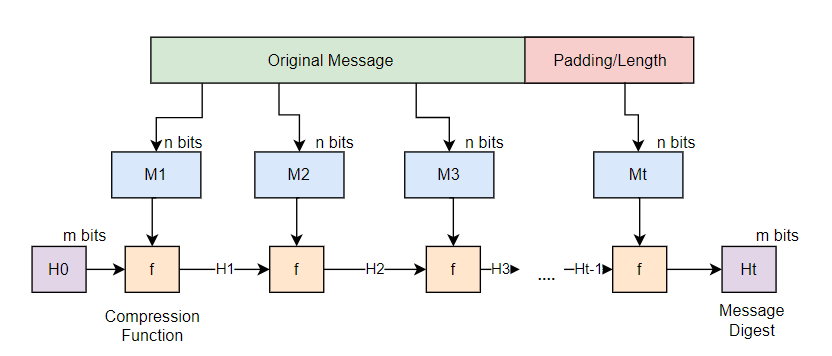
1. 입력된 데이터를 우선 이진 구조로 바꾼다.
2. 이진수로 변환된 데이터는 그 길이가 블록 크기의 배수가 되도록 패딩된다. 이렇게 하면 데이터를 고정된 크기의 블록으로 나눌 수 있다.
3. 해시 함수는 초기 해시 값을 설정한다. 이 값은 알고리즘에 따라 사전에 정의됩니다.
4.각 블록은 순차적으로 처리됩니다. 초기 해시 값 또는 이전 블록의 출력이 다음 블록의 입력으로 사용된다. 각 블록은 압축 함수를 통해 처리된다. 이 함수는 블록의 데이터와 이전 해시 값을 입력으로 받아 새로운 해시 값을 생성한다.
5. 마지막 블록이 처리된 후, 결과 해시 값이 출력된다.
패딩은 입력 데이터를 해시 함수의 블록 크기에 맞게 조정하는 과정이다.
일반적인 패딩 방식은 다음과 같다.
1. 먼저, 입력 데이터의 끝에 '1' 비트를 추가합니다.
2. 그 다음, 필요한 만큼 '0' 비트를 추가하여 데이터의 길이가 블록 크기의 배수가 되도록 만든다. 단, 추가적인 정보(예: 원래 메시지의 길이)를 위한 공간을 남겨둬야 한다.
3. 마지막으로, 원래 메시지의 길이(보통 이진 형태로)를 추가하여 블록을 완성한다. 이 정보는 패딩된 데이터가 원래 데이터와 구별되도록 하는 데 중요한 역할을 한다.
4-2. Miyaguchi-Preneel 구조
Miyaguchi-Preneel 구조에서는 현재 블록의 데이터와 이전 해시 값을 독립적으로 처리하고 그 결과를 결합한다.
구체적으로, Miyaguchi-Preneel 압축 함수는 다음과 같이 동작합니다.
- 현재 블록의 데이터 M와 이전 해시 값 H를 입력으로 받는다.
- M, H, 그리고 M⊕H (여기서 ⊕는 비트 단위 XOR 연산을 나타냄)를 독립적으로 처리한다.
- 이 세 가지 값을 특정 방식으로 결합하여 새로운 해시 값을 생성한다.
