1. 의미
고대 그리스의 수학자 에라토스테네스가 만들어 낸 소수를 찾는 방법
2. 왜 사용하는가?
일단 어떤 알고리즘을 사용하기 위해서는 알고리즘의 사용목적이 중요하다고 생각합니다.
이 알고리즘을 사용하는 이유는 연속된 소수들을 구해야할 때, 간단한 로직으로, 비교적 빠른 시간복잡도를 가져서 코테문제를 풀 때, 많이 사용되는 것 같습니다.
3. 어떻게 쓰는가?
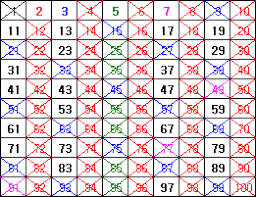
100을 기준으로 설명하겠습니다.
먼저 배열을 0으로 초기화 한 뒤,
- 2부터 2를 제외한 모든 2의 배수들을 1로 바꿉니다.
- 3부터 3을 제외한 모든 3의 배수들을 1로 바꿉니다.
- 4는 1 과정에서 1이 되었기 때문에 넘어갑니다. (왜냐하면, 4의 배수가 2의 배수의 포함되어 있기 때문입니다.)
- 5부터 5를 제외한 모든 5의 배수들을 1로 바꿉니다.
- 6은 1과정에서 1이 되었기 때문에 넘어갑니다. (왜냐하면, 6의 배수가 2의 배수의 포함되어 있기 때문입니다.)
- 7부터 7을 제외한 모든 7의 배수들을 1로 바굽니다.
- 8은 1과정에서 1이 되었기 때문에 넘어갑니다. (왜냐하면, 8의 배수가 2의 배수의 포함되어 있기 때문입니다.)
- 9는 2과정에서 1이 되었기 때문에 넘어갑니다. (왜냐하면, 9의 배수가 3의 배수의 포함되어 있기 때문입니다.)
- 10은 1과정에서 1이 되었기 때문에 넘어갑니다. (왜냐하면, 10의 배수가 2의 배수의 포함되어 있기 때문입니다.)
해당 과정을 10까지 구해주면, 1부터 100까지의 모든 소수를 구할 수 있습니다.
( = 해당 과정을 sqrt(N)까지 해주시면, 1부터 N까지의 모든 소수를 구할 수 있습니다. )
여기서 잠깐..
왜 제곱근까지만 구해주면 끝나나요??
그 이유를 알기 위해서는 그 전에 알아둘 것이 있습니다.
이번에도 100을 예시로 들겠습니다.
그리고 각 숫자들이 어떤 것들을 변하게 했는지 다 나열해보겠습니다.
2 : 4, 6, 8, 10, 12 ~
3 : 6, 9, 12, 15, 18 ~
4 : X
5 : 10, 15, 20, 25 ~
6 : X
7 : 14, 21, 28, 35, 42, 49 ~
8 : X
9 : X
10 : X
자, 이것들을 더 자세히 분해해봅시다. X인것들은 빼고 바꾼 것이 있는 숫자들(소수)만 볼게요.
- 2 : 4(22), 6(23), 8(2*4) ~
- 3 : 6(32), 9(33), 12(3*4) ~
여기서 6은 이미 과정 1에서 1로 변했습니다. - 5 : 10(52), 15(53), 20(54), 25(55)
여기서 10, 15, 20은 각각 과정 1, 2, 1에서 이미 1로 변했습니다. - 7 : 14(72), 21(73), 28(74), 35(75), 42(76), 49(77) ~
여기서 14, 21, 28, 35, 42는 각각 과정 1, 2, 1, 3, 1에서 1로 변했습니다.
이것들로 인해 알 수 있는 점 : 결국에는 소수를 찾은 뒤, 그 수의 제곱부터 변화시키면 된다는 것!!
그래서 왜 제곱근 까지만 구하면 되는데요?
자 마찬가지로 100을 예로 들겠습니다.
100의 제곱근의 다음 소수인 11까지 나열해보겠습니다.
2 : 4부터 2씩 더하면서 100까지 1로 바꾸기
3 : 9부터 3씩 더하면서 100까지 1로 바꾸기
5 : 25부터 5씩 더하면서 100까지 1로 바꾸기
7 : 49부터 7씩 더하면서 100까지 1로 바꾸기
11 : 121부터 11씩 더하면서 100까지 1로 바꾸기 ?????
우리는 1부터 100까지의 소수들을 알고 싶어합니다.
근데 121부터 11의 배수를 바꾸는 것은 하나마나 말짱도루묵인 것입니다.(하나마나)
그래서 결론
1부터 N까지의 소수들을 모두 구할 때, 간단하고 효율적인 에라토스테네스의 체 알고리즘을 쓰자.
1부터 N까지의 소수를 구하려면 구하려는 수의 제곱근까지만 알아보면 된다. 더 알아보면 말짱 도루묵..
소수이면 그것을 소수인 상태라고 그대로 유지해주고, 그 수의 제곱부터 그 수의 배수들을 싹 다 1로 바꾸면 된다.
이 과정을 모두 거친 뒤 배열의 값이 0인 것들이 소수 인 것이다.
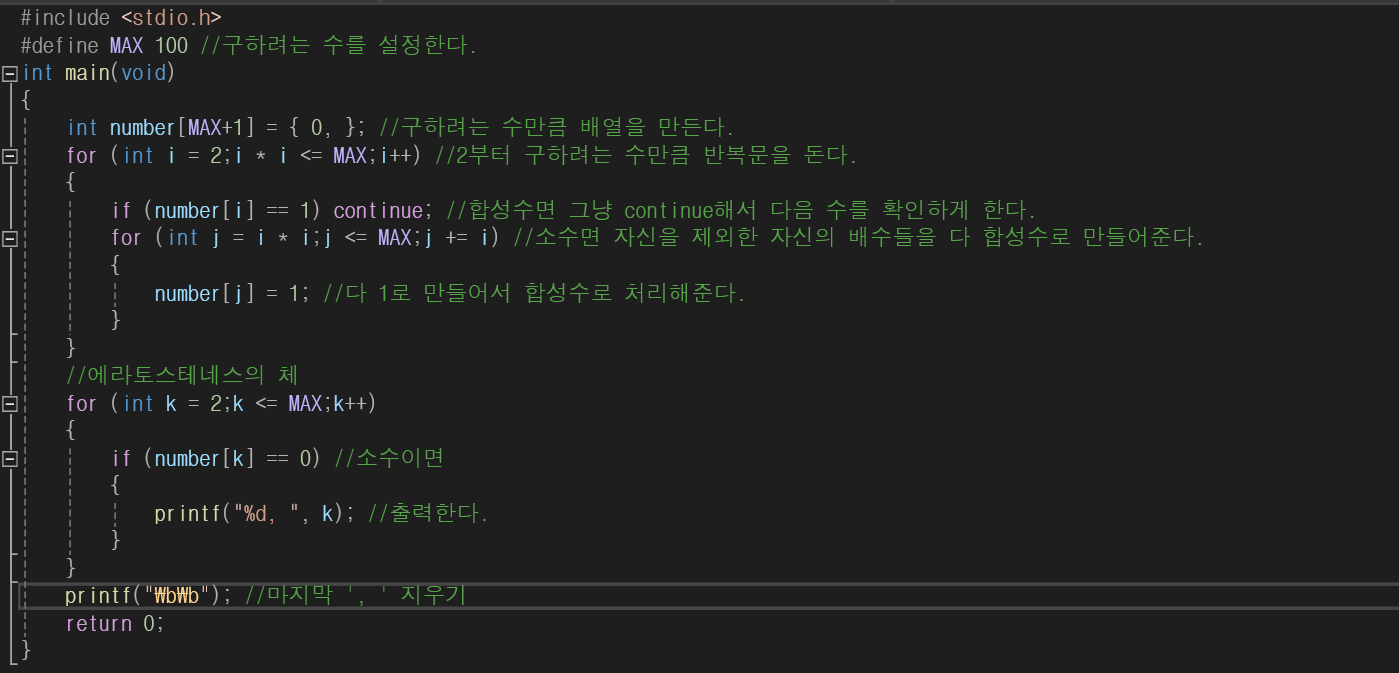
CODE