[Java] 그래프를 탐색하기 위한 인접 행렬과 인접 리스트

: ) YOUNG·2022년 4월 14일

Java algorithm 그래프

자료구조

목록 보기

2/6

서론

최근 다익스트라 알고리즘의 문제를 풀면서 인접리스트를 처음으로 접해서
굉장히 당황스러웠습니다.
그래서 간단하게 정리를 조금 해보고자 합니다.

https://sarah950716.tistory.com/12 해당 글을 참조해서 썼습니다.

본론

인접 행렬

인접행렬은 DFS/BFS 문제에서 많이 볼 수 있는데, 2차원 배열의 형식이라고 생각하면 됩니다.
arr[][]의 형식으로 된 배열이 2차원 배열입니다.

말 그대로 행렬 형식을 배열로 표현하기 위해서 2차원 배열로 생성한 것입니다.

'백준 1012번 유기농배추' 문제의 테스트케이스를 두고 설명을 하자면

위와 같은 테스트케이스가 있다고 해봅시다

우리가 볼 것은 문제를 똑같이 만드는 것은 아니고 테스트케이스로 인접행렬을 만드는 부분만 보면 됩니다.
무방향 그래프를 나타내보면 아래와 같은 그림 처럼 나타낼 수 있습니다.

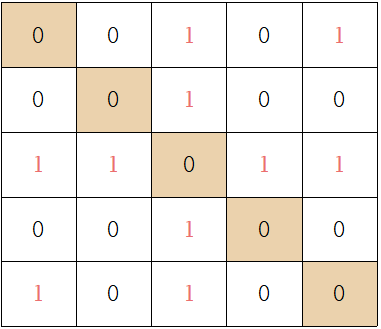
노란색으로 표시된 부분은 자신이기때문에 노란색처리 하고 0으로 표시했습니다.
여기서 특징은 무방향 그래프는 자신을 기점으로 대칭이라는 점입니다.
(0, 2) <-> (2, 0)
(1, 2) <-> (2, 1)
의 형식으로 x,y를 넣어주고 x와 y의 위치를 바꿔서도 넣어 주어야 합니다.

		N = Integer.parseInt(br.readLine()); // 노드의 수
		M = Integer.parseInt(br.readLine()); // 연결된 간선의 수

		arr	= new int[N+1][N+1];

		for(int i=0; i<M; i++) {
			st = new StringTokenizer(br.readLine());
			int y = Integer.parseInt(st.nextToken());
			int x = Integer.parseInt(st.nextToken());
			arr[y][x] = 1;
			arr[x][y] = 1;
		}

코드로 나타내면 위 처럼 만들면 됩니다.

인접 행렬의 장 단점

장점

인접 행렬의 장점은 구현이 쉽다는 점,
노드 i와 노드 j가 연결되어 있는지 확인하고 싶을 때, arr[i][j]가 1인지 0인지만 확인하면 되기 때문에 O(1)이라는 시간 복잡도에 확인할 수 있다는 점

단점

전체 노드의 개수를 V개, 간선의 개수를 E개라고 했을 때, 노드 i에 연결된 모든 노드를 탐색해야 하기 때문에 O(V)의 시간이 걸린다는 단점이 존
만약 노드에 비해 간선이 매우 적을 경우, 적은 간선을 찾기 위해서 전체 노드를 모두 탐색해야 한다는 단점이 있습니다.
최악의 경우, 노드가 억 단위가 된다면, 정말 오랜시간이 걸릴게 될 겁니다.

인접리스트

인접 리스트는 행렬과 다르게 ArrayList의 자료구조를 이용해서 만드는 방식입니다.

먼저 인접행렬과의 차이점으로는 ArrayList는 동적할당이기 때문에 크기를 미리 정해주지 않아도 된다는 특징이 있습니다.

인접 리스트의 형식은 Node class가 있다고 하면 아래와 같이 만들어집니다.

class Node implements Comparable<Node> {
	int end, weight;

	public Node(int end, int weight) {
		this.end = end;
		this.weight = weight;
	}
	
	@Override
	public int compareTo(Node o) {
		return weight - o.weight;
	}
} // End of Node class

List<List<Node>> list; 형식으로 만들어집니다.

우리가 여기서 방향그래프를 인접리스트로 구현 한다고 했을 때, 전체적으로 보면 이렇게 됩니다.

		st = new StringTokenizer(br.readLine());
		V = Integer.parseInt(st.nextToken()); // 정점의 개수
		int E = Integer.parseInt(st.nextToken()); // 간선의 개수
		int K = Integer.parseInt(br.readLine()); // 시작하는 정점
		
		dist = new int[V+1]; // 정점의 갯수 만큼 dist배열 생성
		
		// 인접리스트, dist배열을 전부 최대값인 INF로 초기화시켜줌
		Arrays.fill(dist, INF);

		// 1 ~ V의 정점갯수 만큼 인접list를 생성함. List안에 Node객체형 List를 생성함.
		for(int i=1; i<=V; i++) {
			list.add(new ArrayList<>());
		}

		// 양방향 인접 리스트 구현
		for(int i=0; i<E; i++) {
			st = new StringTokenizer(br.readLine());
			
			int start = Integer.parseInt(st.nextToken());
			int end = Integer.parseInt(st.nextToken());
			int weight = Integer.parseInt(st.nextToken());
			list.get(start).add(new Node(end, weight));
			list.get(end).add(new Node(start, weight));
		}

dist[] 배열을 정점의 개수만큼 초기화를 시켜준뒤
배열의 초기값을 전체 INF인 최대값으로 초기화 해줍니다.

여기서는 최소값으로 초기화를 시켜주기 위함입니다.

이제 list에 Node class 의 객체형 List를 넣기 위해
list를 또 new ArrayList로 초기화 해줍니다.

이 형식이 바로 대표적인 인접리스트 형식이 되는 것입니다.

인접 리스트의 장 단점

장점

인접행렬과 달리, 실제로 연결된 노드들에 대한 정보만 저장
모든 리스트들의 원소의 개수의 합이 간선의 개수와 같다는 점 -> 간선의 개수에 비례하는 메모리만 차지하게 됨
노드 2와 연결된 모든 노드들을 방문해보고 싶다면, 인접 행렬의 경우 arr[2][1], arr[2][2], arr[2][3], arr[2][4]. 총 4번을 확인해보아야 하지만, 인접 리스트의 경우 실제 연결된 노드들만 확인해 볼 수 있기 때문에 arr[2][0] 부터 arr[2][adj[2].size()-1] 까지 총 1번만 확인해보면 된다.

단점

노드 i와 노드 j가 연결되어 있는지 알고 싶다면 arr[i]의 벡터 전체를 돌며, j를 성분으로 갖는지 확인해보아야 합니다.
따라서, 시간 복잡도는 O(V)가 됩니다.
인접 행렬의 경우 arr[i][j]가 1인지 0인지만 확인하면 되기 때문에 O(1)의 시간 복잡도를 갖게됨.