계층적 군집(Hierachical Clustering) 분석
계층적 군집의 개념
✔ 유사한 개체를 군집화하는 과정을 반복하여 군집을 형성하는 방법이다.
✔ 두 개체 간의 거리에 기반하여 군집을 형성해 나가므로 거리에 대한 정의가 필요하다
✔ 계층적 군집분석은 개수를 미리 정하지 않음.
✔ n개의 군집으로 시작해 점차 줄여서 하나의 군집만이 남을 때 까지 병합을 함
✔ linkage clustering은 계층적 군집분석 방법 중 하나이다.
계층적 군집을 형성하는 방법
| 병합적 방법 Agglomerative | - 작은 군집으로 부터 시작하여 군집을 병합하는 - 거리가 가까우면서 유사성이 높음 |
| 분할적 방법 Divisive | - 큰 군집으로부터 출발하여 군집을 분리해 나가는 방법 - R 언어에서 cluster 패키지의 diana(), mona() 함수 이용 |
군집 간의 거리측정 방법
- 군집간의 연결법에 따라 군집의 결과가 달라질 수 있다.
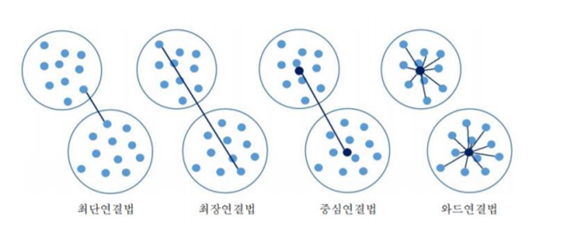
최단연결법 Single Linkage Method (단일 연결법 (Single Linkage Method))
-
n * n거리행렬에서 거리가 가장 가까운 데이터를 묶어서 군집을 형성한다.
-
군집과 군집 또는 데이터와 거리 계산시 최단거리(min)를 거리로 계산하여 거리행렬 수정을 진행한다.
-
수정된 거리행렬에서 거리가 가까운 데이터 또는 군집을 새로운 군집으로 형성한다.
-
최솟값으로 측정
최장연결법 (Complete Linkage Method)
-
두 군집 사이의 거리를 각 군집에서 하나씩 관측값을 뽑았을 때 나타날 수 있는 거리의 최댓값으로 측정
-
군집에서 하나씩 관측값을 뽑았을 때 나타날 수 있는 거리의 최댓값으로 측정하여 가장 유사성이 큰 군집으로 병합해 나가는 방법
-
최댓값으로 측정
중심연결법 (Centroid Linkage Method)
-
두 군집의 중심 간의 거리를 측정
-
두 군집이 결합될 때 새로운 군집의 평균은 가중 평균을 통해 구함
-
계산량이 적고, 중심 사이의 거리를 한번만 계산
-
두 군집 중심간 거리
평균연결법 (Average Linkage Method)
-
모든 항목에 대한 거리를 평균을 구하면서 가장 유사성이 큰 군집을 병합해 나가는 방법
-
계산량이 불필요하게 많아질 수 있음
-
모든 항목의 거리평균
-
단일연결법과 완전연결법보다 이상치에 덜 민감
와드연결법 (Ward Linkage Method) ⭐⭐⭐
-
군집내 편차들의 제곱합을 고려한 방법이다.
-
병합된 군집의 오차제곱합이 병합 이전 군집의 오차제곱합에 비해 증가한 정도가 작아지는 방향으로 군집을 형성하는 방법
-
군집 간 정보의 손실을 최소화하기 위해 군집화를 진행한다.
-
군집내 오차제곱합(SSE)
비계층적 군집(K-means Clustering) 분석
K-means 군집분석 개념
✔ 주어진 데이터를 k개의 군집으로 묶는 알고리즘으로 k개 만큼 군집 수를 초기 값으로 지정하고, 각 개체를 가까운 초깃값에 할당하여 군집을 형성
✔ 초기값 선택이 최종 군집 선택에 영향을 미친다.
✔ 초기값 선택이 어려움
✔ 한 개체가 속해있던 군집에서 다른 군집으로 이동해 재배치가 가능
✔ 간혹 최적해에 도달하지 못할 수 도 있다.
✔ 잡은(노이즈)나 이상값에 영향을 많이 받는다.
✔ 결과 해석이 어렵다.
✔ 연속형 변수의 거리 측정만 다룰 수 있다.
K-평균 군집 k값 선정 기법 ⭐⭐⭐⭐
| 엘보우 기법 | - x축에 클러스터의 개수(k값)를 y축에 SSE 값을 두었을 때 기울기가 완만한 부분(팔꿈치 부분)에 해당하는 클러스터를 선택하는 기법 - k-평균 군집 알고리즘을 통해 K값을 구하는 기법 - 클러스터 내 오차제곱합이 최소가 되도록 클러스터의 중심을 결정해 나가는 방법 - 클러스터 개수를 늘렸을 때, 중심 간의 평균 거리가 더 이상 많이 감소하지 않는 경우의 k를 선택한다. |
| 실루엣 기법 | - 각 군집 간의 거리가 얼마나 분리되어 있는지를 나타내는 기법 - 실루엣 계수는 1에 가까울수록 군집 간 거리가 멀어서 최적화가 잘 되어 있다고 할 수 있고, 0에 가까울수록 군집 간 거리가 가까워서 최적화가 잘 안되어 있다고 할 수 있다. |
| 덴드로그램 | - 군집의 개체들이 결합되는 순서를 나타내는 트리 형태의 구조이다. - 덴드로그램 시각화를 이용하여 군집의 개수를 결정한다. - 계층적 군집 분석의 덴드로그램 시각화를 이용하여 군집의 개수 결정 |
실루엣 계수 ⭐⭐⭐⭐
- 군집분석의 품질을 정량적으로 평가하는 대표적인 지표로 군집 내의 데이터 응집도와 군집간의 분리도를 계산하여 군집 내의 데이터의 거리가 짧을수록, 군집 간 거리가 멀수록 값이 커지며 완벽한 분리일 경우 1의 값을 가지는 지표
- 군집분할의 성과를 평가하는 것
- 군집 모형 평가 기준 중 하나이며 군집의 밀집정도를 계산하는 방법으로 군집 내의 거리와 군집 간의 거리를 기준으로 군집 분할의 성과를 평가하는 것

