
백준 17835번
https://www.acmicpc.net/problem/17835
문제
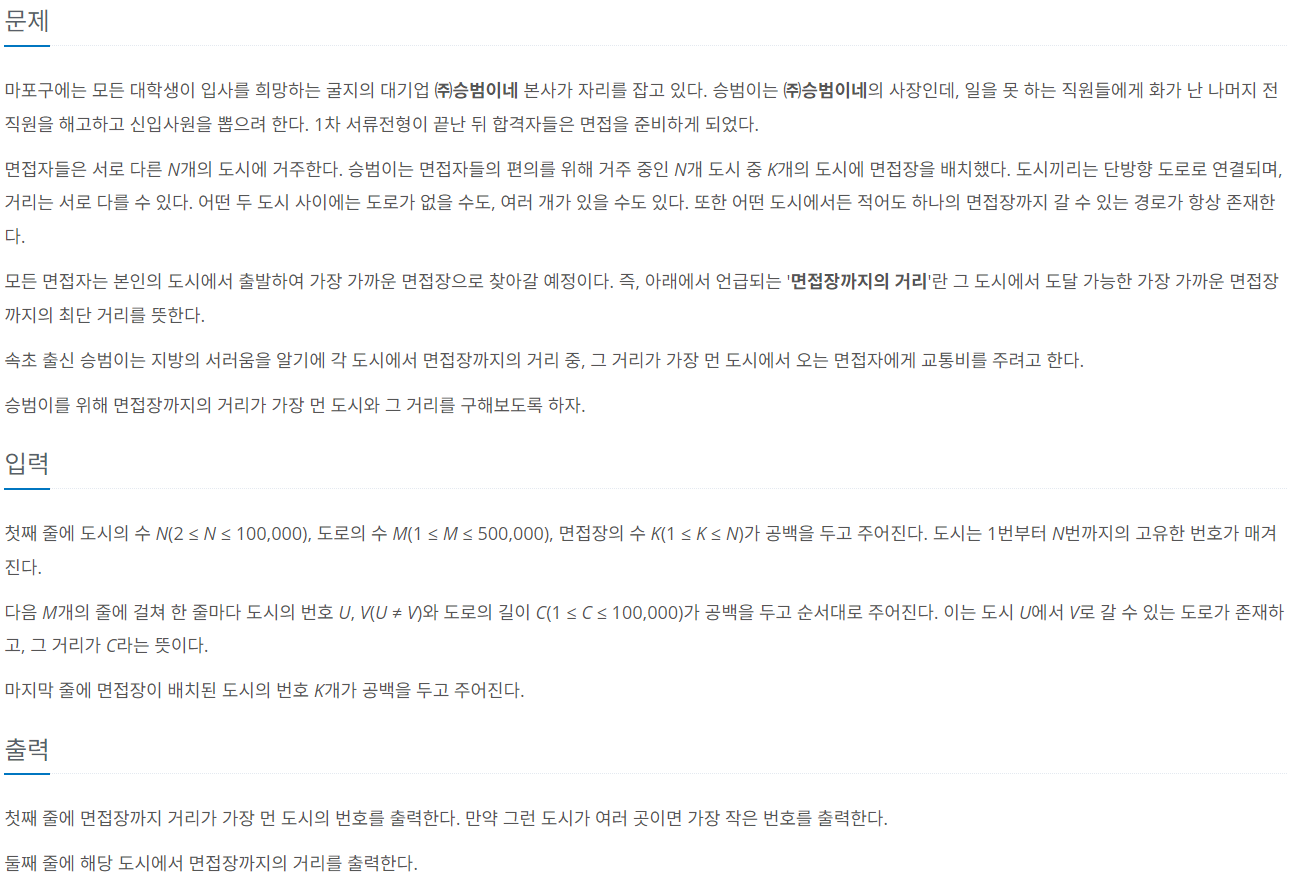
생각하기
-
다익스트라 문제이다.
- 멀티 소스 다익스트라 문제이다.
-
다익스트라 문제중에 진짜 괜찮은 문제인 것 같음
-
문제이해를 잘해야 코드가 왜 이렇게 되는지도 이해할 수 있다.
동작
해당 문제는 역방향을 활용해야 한다. 그렇다면 어떤 부분에서 역방향임을 유추할 수 있을까
여러 개의 도착지점을 동시에 고려해야 하므로, 다중(멀티)소스 다익스트라를 생각해야 한다.
멀티 소스 다익스트라를 구현할 때, 출발점들을 한꺼번에 우선순위 큐에 넣고 최단 거리를 갱신해 나가는 로직을 쓰면 되는데, 이는 "역방향 그래프"에서 하면 곧바로 원하는 거리를 얻을 수 있다.
모든 도시 -> K개의 면접장
K개의 면접장 -> 모든 도시
훨씬 더 효율적이다.
⭐ 이문제의 핵심은 문제에서 어떤 도시에서든 하나의 면접장까지 갈 수 있는 경로가 항상 존재한다. 이 문장이다.
왜 이 문장이 중요하냐 -> 바로 단방향 그래프이기 때문이다.
N개의 각 도시에서 K개의 면접장까지 최단 거리를 구하려면, N 번의 다익스트라를 해야되는데 이러면 시간이 오래걸린다.
대략 -> 정도라고 하는데... 아무튼 그렇다
이렇게 하면 시간이 너무 오래걸려서 계산을 할 수 없기 때문에 어쨌든 N보다 작거나 같을 K에서 N까지의 거리를 구하면 한번의 다익스트라를 실행하면 문제를 해결할 수 있다.
각 면접장 노드를 PriorityQueue에 모두 넣으면 가장 가까운 노드를 갱신하면서 찾아가기 때문이다. 이렇게 하면 자연스럽게 각 노드별로 가장 가까운 면접장을 찾을 수 있다.
이게 단방향 그래프이기 때문과 어떤 도시에서는 하나의 면접장으로 이어지는 길이 있는 점을 거꾸로 돌려서 어떤 면접장이든 하나의 도시로는 갈 수 있다로 변경하는 것이다. 그래서 역방향으로 노드를 변경하는 것이다.
즉, 문제에서는 U -> V 이지만, V -> U로 구현하는 것이다.
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
adjList.get(v).add(new Edge(u, c));
}
이후에 각 면접장에서 출발 할 수 있도록 모두 pque에 넣는다.
for (int i = 0; i < K; i++) {
int temp = Integer.parseInt(st.nextToken());
dist[temp] = 0;
pque.offer(new Edge(temp, 0));
}
각 면접장에서 출발하므로 dist[temp]는 똑같이 0으로 해주고~
이 다음은 똑같이 다익스트라 실행하면 면접장에서 출발해서 각 노드별 최단거리를 구할 수 있다.
dijkstra();
for (int i = 1; i <= N; i++) {
if (maxDist < dist[i]) {
maxDist = dist[i];
ansNum = i;
}
}
결과

코드
import java.io.*;
import java.util.*;
public class Main {
// input
private static BufferedReader br;
// variables
private static int N, M, K;
private static List<List<Edge>> adjList;
private static int[] interviewRooms;
private static final long INF = Long.MAX_VALUE;
private static class Edge implements Comparable<Edge> {
int num;
long dist;
private Edge(int num, long dist) {
this.num = num;
this.dist = dist;
}
@Override
public int compareTo(Edge o) {
return Long.compare(dist, o.dist);
}
} // End of Edge class
public static void main(String[] args) throws IOException {
br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
input();
bw.write(solve());
bw.close();
} // End of main()
private static String solve() {
StringBuilder sb = new StringBuilder();
long[] ret = BFS();
long max = -1;
int num = 0;
for (int i = 1; i <= N; i++) {
if (ret[i] != INF) {
if (max < ret[i]) {
max = ret[i];
num = i;
}
}
}
sb.append(num).append('\n').append(max);
return sb.toString();
} // End of solve()
private static long[] BFS() {
PriorityQueue<Edge> que = new PriorityQueue<>();
long[] dists = new long[N + 1];
boolean[] isVisited = new boolean[N + 1];
Arrays.fill(dists, INF);
for (int t : interviewRooms) {
que.offer(new Edge(t, 0));
dists[t] = 0;
}
while (!que.isEmpty()) {
Edge cur = que.poll();
if (isVisited[cur.num]) continue;
if (cur.dist > dists[cur.num]) continue;
isVisited[cur.num] = true;
for (Edge next : adjList.get(cur.num)) {
if (dists[next.num] > dists[cur.num] + next.dist) {
dists[next.num] = dists[cur.num] + next.dist;
que.offer(new Edge(next.num, dists[next.num]));
}
}
}
return dists;
} // End of BFS()
private static void input() throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
adjList = new ArrayList<>();
for (int i = 0; i <= N; i++) {
adjList.add(new ArrayList<>());
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
adjList.get(v).add(new Edge(u, w));
}
interviewRooms = new int[K];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < K; i++) {
interviewRooms[i] = Integer.parseInt(st.nextToken());
}
} // End of input()
} // End of Main class
