1번

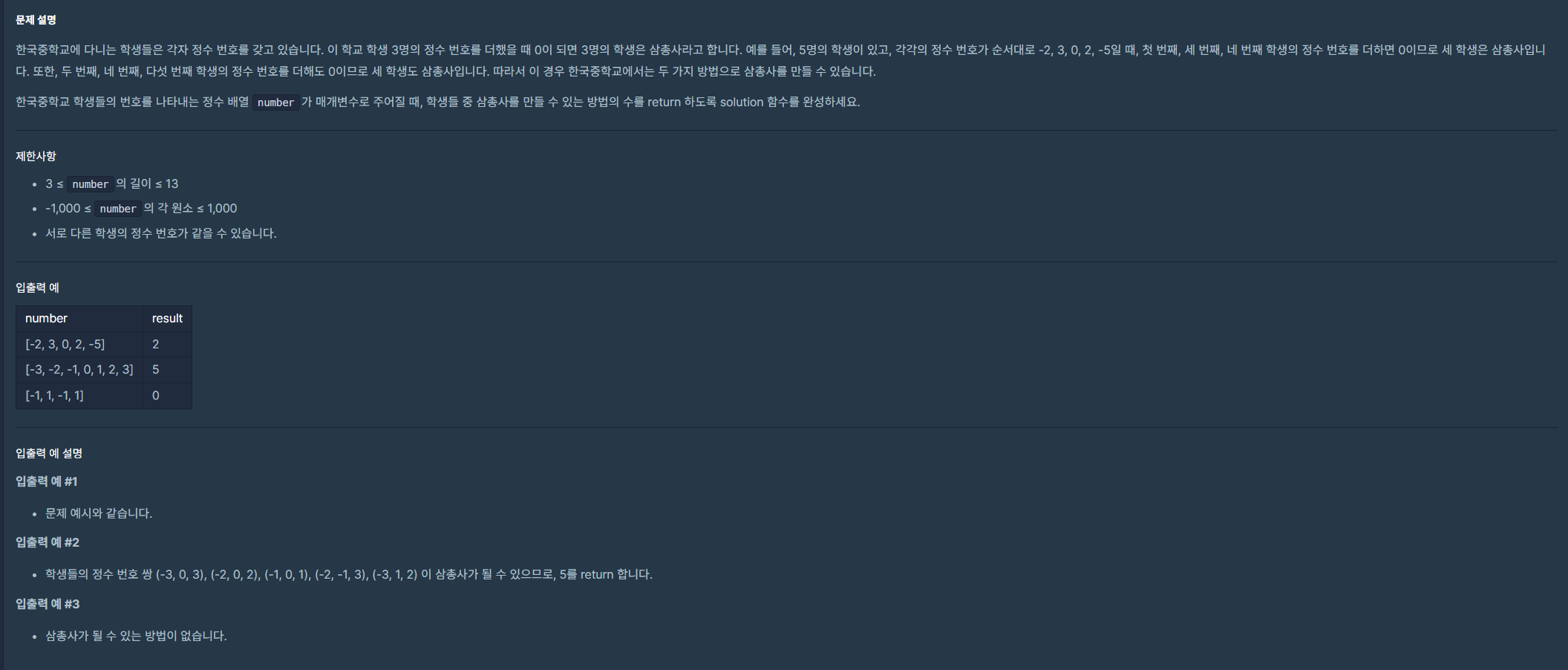
생각하기

---

• 간단한 백트래킹 문제였다.
  • 중복을 포함하지 않기 위해서 DFS메소드에서 idx 매개변수를 줬다.

동작

		if(depth == 3) {
			int sum = 0;
			for(int i=0; i<3; i++) {
				sum += ans[i];
			}
			
			if(sum == 0) {
				resultCount++;
			}
			
			return;
		}

재귀의 깊이를 삼총사의 값인 3으로 설정해서 깊이가 3일때마다 계산을 해서 총합이 0이면 결과값을 담을 resultCount를++ 하도록 설정했다.

코드

public class Solution {
	static int ans[] = new int[3];
	static int numArr[];
	static int N;
	static int resultCount = 0;

	public int solution(int[] number) {
		N = number.length;
		numArr = number;
		
		DFS(0, 0);
		return resultCount;
	} // End of solution
	
	private static void DFS(int idx, int depth) {
		if(depth == 3) {
			int sum = 0;
			for(int i=0; i<3; i++) {
				sum += ans[i];
			}
			
			if(sum == 0) {
				resultCount++;
			}
			
			return;
		}
		
		
		for(int i=idx; i<N; i++) {
			ans[depth] = numArr[i];
			DFS(i+1, depth + 1);
		}
	} // End of DFS
} // End of Main class

---

2번

틀렸다가 다시 풀었음

생각하기

• 특별한 알고리즘은 없고, 효율성을 생각해야 하는 문제였다.
  • 2중 for문을 사용할 경우, 시간초과 발생한다고 생각한다.
  • 결국, 2중 for문을 사용하지 않고 바깥에 for문을 나열하는 방법을 생각해야 한다.

• 철수에게 먼저 전체 케이크를 주고, 동생에게 분배하는 방법을 선택했다.
  • 철수에게 케이크를 주면서 전체 토핑의 정보를 파악하는 for 문을 만든다.
  • 동생에게 분배하면서 동생의 토핑 개수를 파악하는 for문을 만든다. 여기서 철수의 토핑개수를 빼준다.

• 번외: 처음에 Set을 써서 중복을 제거하려는 방법을 택했는데, 시간초과가 발생했다.

  • 2중 for문을 사용한게 문제였다.

  • set을 쓰지않아도 해결 할 수 있는 문제이긴 하다.

  • 그래도 데이터양이 많아 지고나서 배열이 시간이 더 빠른게 결과에서 드러남

  • 그리고 Set을 쓸거면 성능이 가장 좋은 HashSet을 추천함 (정렬이 필요하면 TreeSet)

    

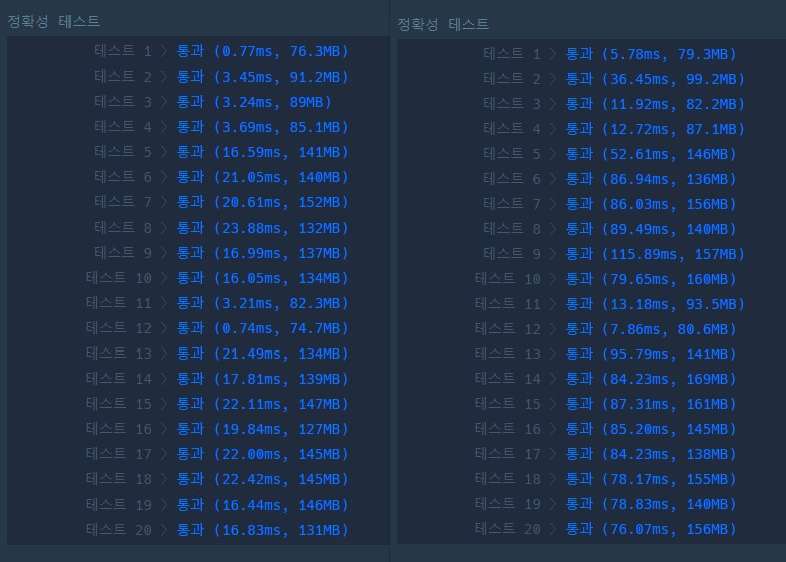
배열 ↑                          HashSet ↑

동작

		int cheolsuArr[] = new int[len+1];
		int brotherArr[] = new int[len+1];

먼저 topping 배열의 정보를 담을 수 있는 배열을 미리 만들어준다.
철수와 동생의 배열 2개를 만든다.

		int cheolsuCount = 0;
		int brotherCount = 0;
		for (int i = 0; i < len; i++) {
			if(cheolsuArr[topping[i]] == 0) {
				cheolsuCount++;
			}
			cheolsuArr[topping[i]]++;
		}

철수와 동생이 가지고 있는 토핑의 개수를 파악할 변수 cheolsuCount ,brotherCount 를 만들어준다.

그리고 철수한테 토핑을 전부 준다.
topping[i]의 값을 인덱스로 설정해서 해당 자리의 값이 0일 경우, 철수가 가지고 있는 토핑의 개수를 증가시킨다.

하지만 중복을 체크해야 되기 때문에 인덱스자리의 값은 0이 아니더라도 계속 증가시킨다.

		for(int i=0; i<len; i++) {
			if(brotherArr[topping[i]] == 0) {
				brotherCount++;
			}
			brotherArr[topping[i]]++;
			cheolsuArr[topping[i]]--;
			
			if(cheolsuArr[topping[i]] == 0) {
				cheolsuCount--;
			}
			if(cheolsuCount == brotherCount) result++;
		}

이제 다시 topping의 배열을 순회하면서
아무 토핑도 가지지 않은 동생에게 토핑을 나눠 준다는 형식이다. 현재 토핑은 철수가 모두 가지고 있기 때문에 이 토핑을 동생에게 주고 철수가 가지고 있는 토핑을 하나씩 제거한다는 개념을 적용하면 된다.

철수가 가지고 있는 토핑 인덱스의 값이 0이 되면 더이상 해당 토핑이 없기 때문에 cheolsuCount를 -1 해준다.

또 동생의 토핑인덱스값이 0에서 증가하는 경우, 토핑이 새로 생기는 것이기 때문에 brotherCount을 +1 해준다.

코드

배열

public class Solution {
	public int solution(int[] topping) {
		int len = topping.length;
		int result = 0;
		int cheolsuArr[] = new int[len+1];
		int brotherArr[] = new int[len+1];

		int cheolsuCount = 0;
		int brotherCount = 0;
		for (int i = 0; i < len; i++) {
			if(cheolsuArr[topping[i]] == 0) {
				cheolsuCount++;
			}
			cheolsuArr[topping[i]]++;
		}
	
		
		for(int i=0; i<len; i++) {
			if(brotherArr[topping[i]] == 0) {
				brotherCount++;
			}
			brotherArr[topping[i]]++;
			cheolsuArr[topping[i]]--;
			
			if(cheolsuArr[topping[i]] == 0) {
				cheolsuCount--;
			}
			if(cheolsuCount == brotherCount) result++;
		}
		
		
		return result;
	} // End of solution
} // End of Main class

Set

import java.util.HashSet;

public class Solution {
	public int solution(int[] topping) {
		int len = topping.length;
		int result = 0;
		int cheolsuArr[] = new int[len + 1];
		int brotherArr[] = new int[len + 1];

		HashSet<Integer> cheolsuSet = new HashSet<>();
		HashSet<Integer> brotherSet = new HashSet<>();

		for (int i = 0; i < len; i++) {
			cheolsuSet.add(topping[i]);
			cheolsuArr[topping[i]]++;
		}
		
		for (int i = 0; i < len; i++) {
			brotherSet.add(topping[i]);

			brotherArr[topping[i]]++;
			cheolsuArr[topping[i]]--;
			
			if (cheolsuArr[topping[i]] == 0) {
				cheolsuSet.remove(topping[i]);
			}

			if (cheolsuSet.size() == brotherSet.size())
				result++;
		}

		return result;
	} // End of solution
} // End of Main class