정상 시계열
: 대부분의 시계열 자료는 다루기 어려운 비정상성 시계열 자료이기 때문에 분석하기 쉬운 정상성 시계열 자료로 변환해야 함
(약) 정상성 (weak stationary) 조건
1. yt의 평균이 모든 t에 대해서 동일 (시간의 추이와 관계없이 평균이 일정)
→ 평균이 일정하지 않은 시계열은 차분을 통해 정상화
2. yt의 분산이 모든 t에 대해서 동일 (시간의 추이와 관계없이 분산이 일정)
→ 분산이 일정하지 않은 시계열은 로그 변환을 통해 정상화
3. yt와 yt-h의 공분산이 모든 t에 대해서 동일 (두 시점 간의 공분산이 기준시점과 무관)
→ yt와 ys 간의 공분산은 시차 |t-s|에만 의존하고 시점 t와 s에는 의존하지 않음
ex) 6단위만큼 시점 차이가 나는 경우, Cov(Y1, Y7) = Cov(Y11, Y17)
백색잡음 (White noise)
: 평균이 0, 분산 σ^2을 가지는 자기상관이 없는 시계열로, 서로 다른 두 시점 사이의 yt값들 사이의 상관계수가 0인 경우
: 시점 t와 무관하므로 항상 정상성을 만족하는 정상 시계열
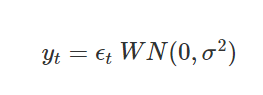
: ACF, PACF가 모든 시차에 걸쳐 유의하지 않으며 어떤 특징도 보이지 않음
확률보행 (Random walk)
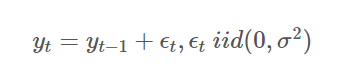
: t 시점의 y값이 t-1 시점의 y값과 t 시점의 오차항에 의해 결정되는 시계열 모형
: 1차 차분하면 백색잡음 계열
E(yt) = E(ε1+ε2+ … + εt) = 0
V(yt) = Var(ε1) + Var(ε2) + … + Var(εt) = tσ^2
: 시간에 따른 편차의 평균은 0이지만 분산은 시간 t에 비례하여 증가하므로 비정상 시계열
: ACF는 매우 느리게 감소하는 특징을 가지며, PACF는 모든 시차에서 유의하지 않으며 어떤 특징도 보이지 않음
표류가 있는 확률보행 (Random walk with drift)
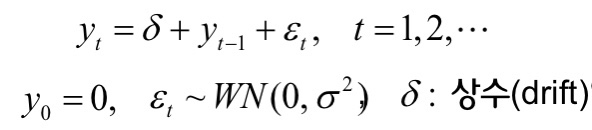
: 확률보행 모델에 상수항과 시간적 추이가 추가된 모형
: 1차 차분하면 상수항이 평균인 백색잡음 계열
E(yt) = E(α+ ε1+ε2+ … + α+ εt) = Σ α
V(yt) = Var(y0 + α + ε1+ … + α + εt) = Σ σ^2
: 평균, 분산이 모두 무한히 커지므로 비정상 시계열
: 상수항이 0보다 큰 (양) 경우 상방으로, 0보다 작은 경우 하방으로 흘러감
ACF와 PACF
- 자기공분산함수
r(h) = Cov(yt, yt-h) = E[(yt-μ)(yt-h-μ)]
: 같은 수에서 서로 다른 시점 (t, t-h) 과의 공분산
r(0) = Var(yt)
→ h=ㅇ이면 동일시점이므로 그 시점에서의 분산을 의미
r(-h) = r(h) - 자기상관함수 (autocorrelation function, acf)
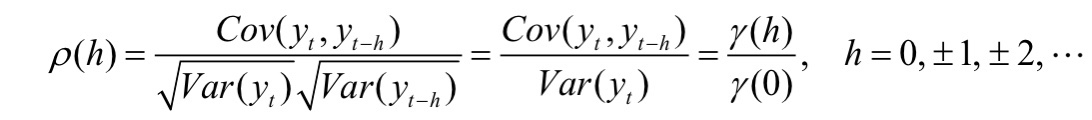
: 자기공분산을 정규화한 것으로, ~1과 1사이의 값
: 시차 h에 대해서, 두 시계열 확률변수 (시점) 간 상관관계
ρ(0) = 1 → ACF에서 시점 0의 값은 자기 자신과의 상관성을 나타내므로 1, 해석 시 해당 부분은 제외하고 해석
ρ(-h) = ρ(h)
- 편자기상관함수 (partial autocorrelation function, pacf)
: 어떤 것들에 대한 상관관계를 보려고 할 때, 그에 영향을 주는 요소들을 제외하고 상관관계를 확인
: Corr(yt, yt-k | yt-1, … , yt-k+1)
→ 서로 다른 두 시점 사이의 관계를 분석할 때 중간에 있는 값들의 영향은 제외
