생각 정리
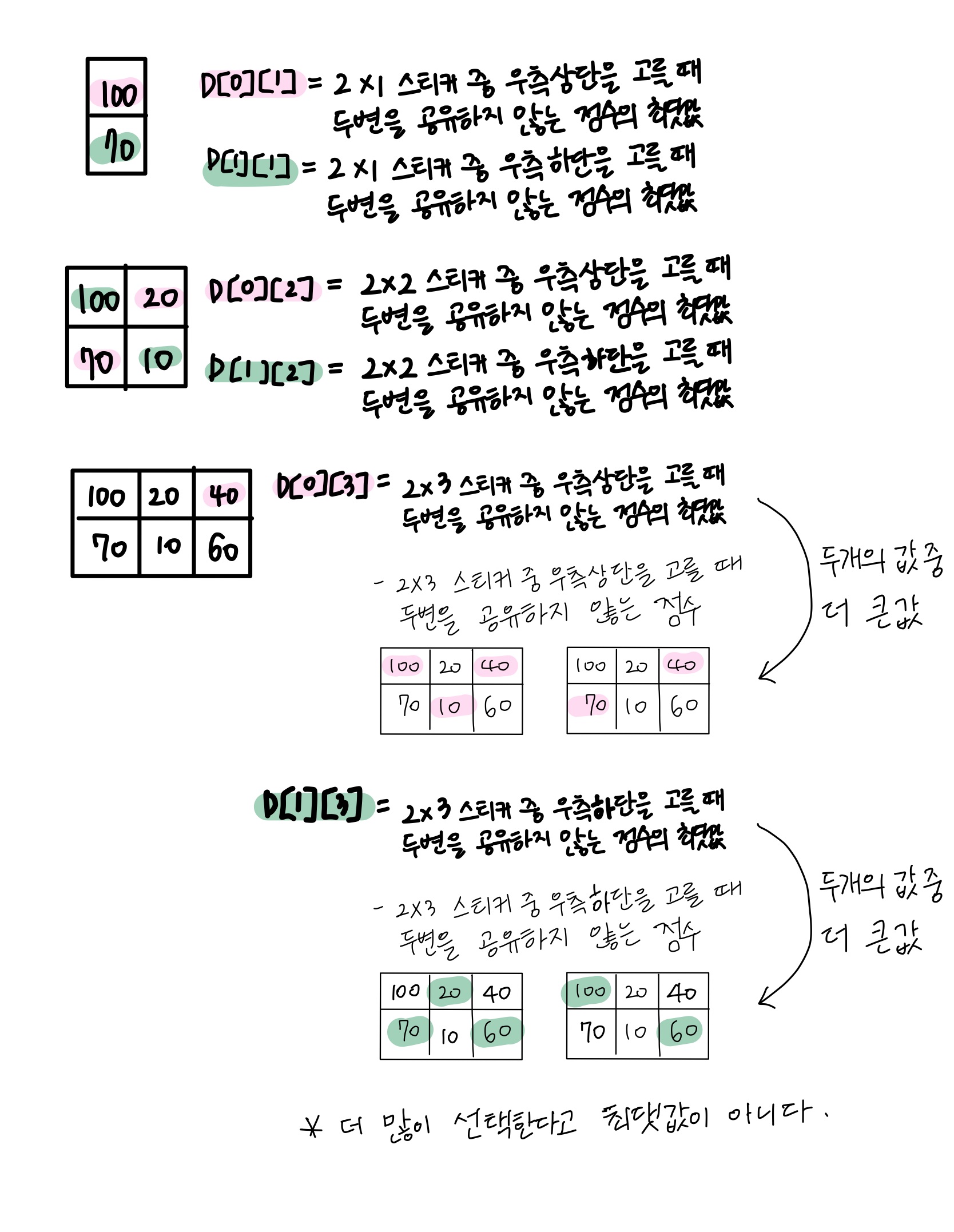
D[N] = 2 X N개의 스티커 중 두변을 공유하지 않는 스티커 정수의 최댓값
D[3]을 생각하는 과정에서 막혔다.
생각하지 못한 것
2 X N개의 스티커에 대해서 D[0][N], D[1][N] 두가지로 나누어 생각하기
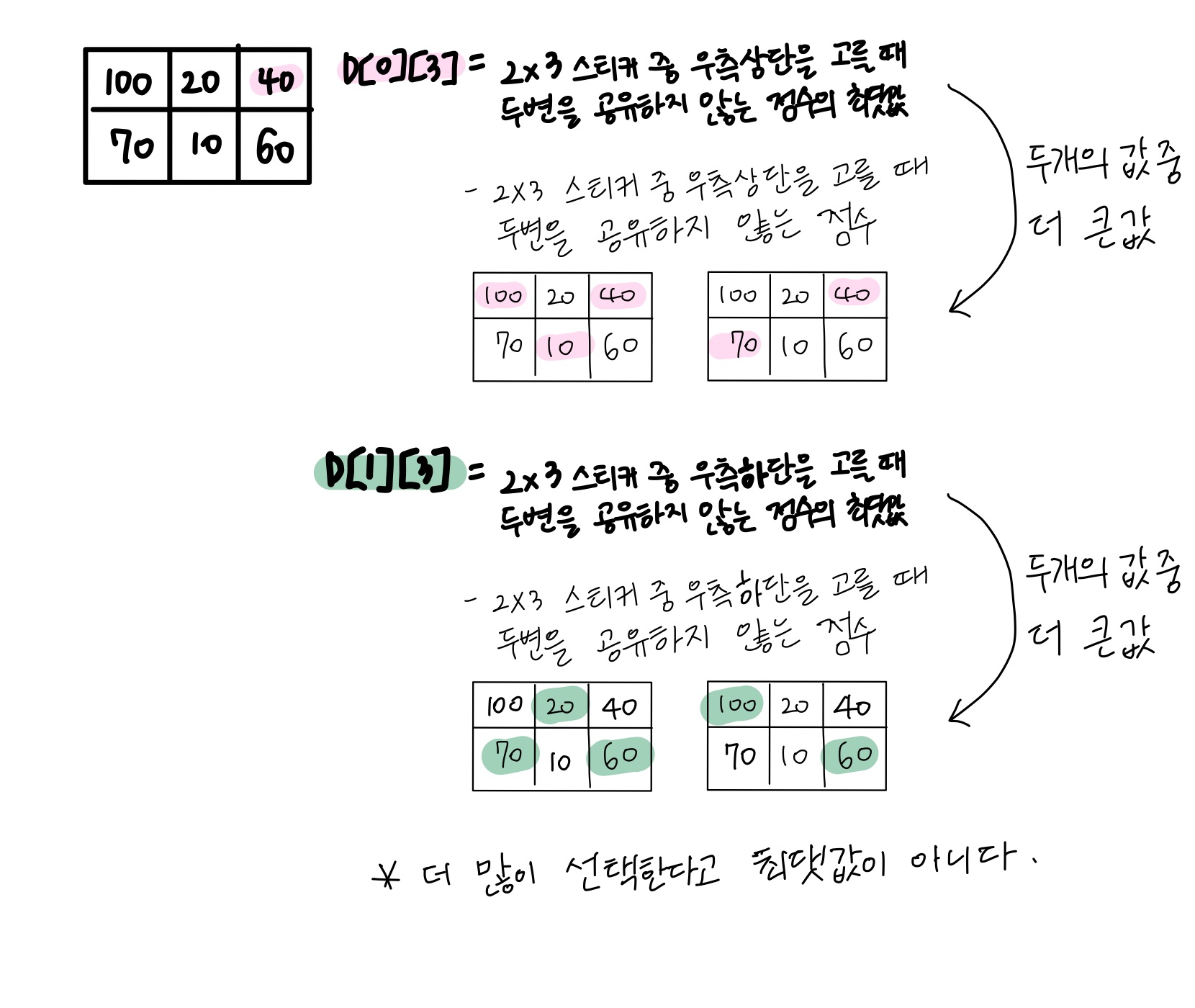
- D[0][N] = 2 X N개의 스티커 중 오른쪽 상단을 선택했을 때 두변을 공유하지 않는 스티커 정수의 최댓값
- D[1][N] = 2 X N개의 스티커 중 오른쪽 하단을 선택했을 때 두변을 공유하지 않는 스티커 정수의 최댓값
D[N] = D[0][N]과 D[1][N] 중 큰 값
그렇다면, D[0][N]과 D[1][N]은 어떻게 구할까 ? N이 3일때의 경우를 나타내 보았다.
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
for(int i=0; i<T; i++) {
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[2][n];
int[][] D = new int[2][n];
for(int j=0; j<2; j++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for(int k=0; k<n; k++) {
arr[j][k] = Integer.parseInt(st.nextToken());
}
}
//arr[0][j] j번째 스티커의 위쪽 숫자, arr[1][j] j번째 스티커의 아래쪽 숫자
for(int j= 0; j<n; j++) {
if(j == 0){
D[0][0] = arr[0][0];
D[1][0] = arr[1][0];
}
else if(j == 1) {
D[0][1] = D[1][0] + arr[0][1];
D[1][1] = D[0][0] + arr[1][1];
}
else {
D[0][j] = Math.max(D[1][j-2] , D[1][j-1]) + arr[0][j];
D[1][j] = Math.max(D[0][j-2] , D[0][j-1]) + arr[1][j];
}
}
System.out.println(Math.max(D[0][n-1], D[1][n-1]));
}
}
}
