해시 함수
- 해시 함수: 임의의 길이를 갖는 임의의 데이터에 대해 고정된 길이의 데이터로 매핑하는 함수
- 충돌: 서로 다른 임의의 문자열이 같은 문자열로 변환되는 것(입력이 다름에도 드물게 동일한 값을 출력되는 경우)
- 키: 매핑 전 원래 데이터 값
- 해시 값: 매핑 후 데이터 값
- 해시 테이블:
- 해싱: 매핑하는 과정
- 적재율: 해시 테이블의 크기 대비 키의 개수,
키의 개수: K, 해시 테이블의 크기: N이면 적재율: K/N
ex) 해시 함수 H에서 H(Lisa Smith) = 01

해시 충돌
- 서로 다른 문자열을 해시한 결과가 동일한 경우
- 해시 함수 H에서 서로 다른 문자열 s1과 s2에 대해서 H(s1) = H(s2)인 경우
해시 특징
- 시스템 자원 소모가 적음
- 같은 입력 값에 대해서 같은 출력 값 보장
** 특수 목적으로 같은 입력에 대해 다른 출력 값을 가지는 해시 함수도 존재 - 효율적인 데이터 관리: 적은 리소스로 많은 데이터를 효율적으로 관리
- 빠른 데이터 처리: 색인(index)에 해시 값을 사용하여 정렬을 하지 않고, 모든 데이터를 살피지 않아도 검색, 삽입, 삭제를 빠르게 수행 가능
해시 테이블은 테이블의 크기에 상관없이 색인을 알면 데이터에 빠르게 접근 가능, 색인은 계산이 간단한 함수(상수 시간)로 작동하기 때문에 효율적
시간 복잡도
- 데이터 탐색, 삽입, 삭제 시 O(1)의 시간 복잡도를 갖는다.
해시 테이블
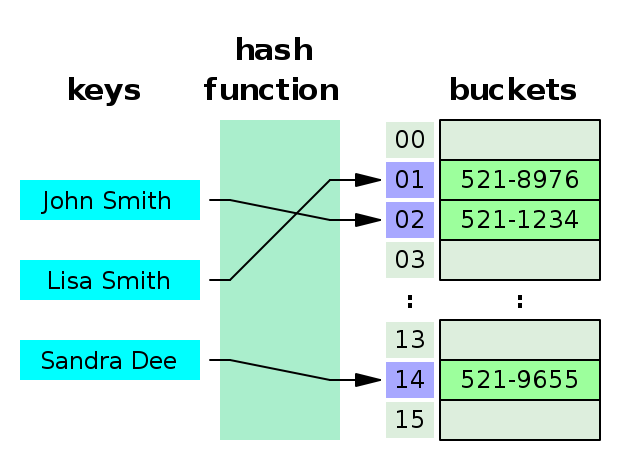
- 해시함수를 사용하여 변환한 값을 색인(index)으로 삼아 키(key)와 데이터(value)를 저장하는 자료구조
- 리스트를 사용하는 접근법은 동일하나 색인 개념이 추가되었다.
- 버킷, 슬롯: 색인 주소 값의 데이터가 저장되는 곳
- 해시 테이블을 구현할 때 해시 충돌이 일어나게 되면 체이닝(Chaining) 또는 개방주소법(Open Addressing)을 통해서 해결해야 한다.
한계점
- 최대 키 값에 대해 알고 있어야 한다.
- 최대 키 값이 작을 때 실용적으로 사용할 수 있다.
- 키 값이 골고루 분포되어있지 않으면 메모리 낭비가 심하다.
* 충돌 해결법
개방주소법(Open Addressing)
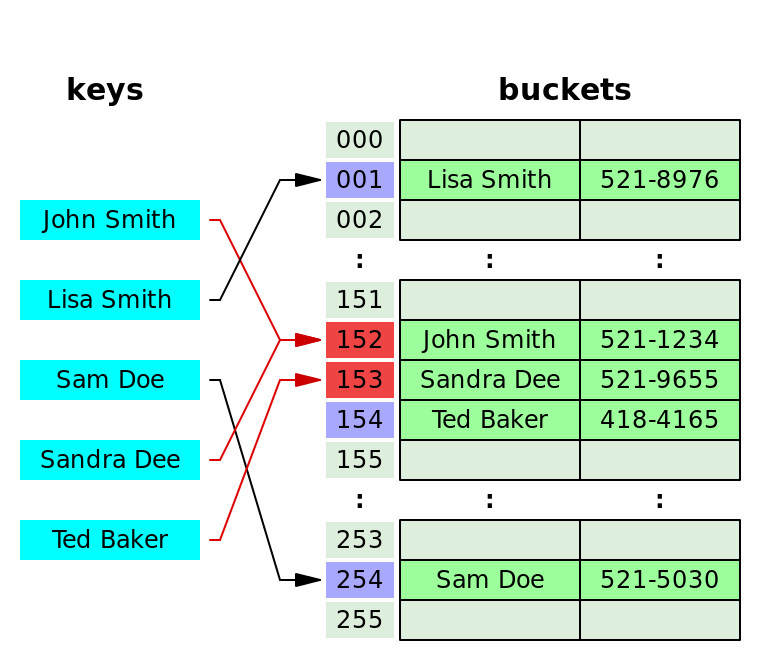
- 이전의 결과를 버리지 않고 저장하나 리스트를 붙여서 저장하는 방식이 아닌 모든 원소를 해시 테이블 내부에 저장하는 방식
-> 테이블 크기가 반드시 데이터의 개수보다 커야 한다. - 충돌이 일어난 인덱스를 건너뛰어 빈 공간이 있는지 탐색 후 진입
- 인덱스만 증가시켜주면 되기 때문에 안정적
- 삽입: 계산한 해시 값에 대한 인덱스가 이미 차있는 경우 다음 인덱스로 이동하면서 비어있는 곳에 저장한다. 이렇게 비어있는 자리를 탐색하는 것을 탐사(Probing)라고 한다.
- 탐색: 계산한 해시 값에 대한 인덱스부터 검사하며 탐사를 해나가는데 이 때 “삭제” 표시가 있는 부분은 지나간다.
- 삭제: 탐색을 통해 해당 값을 찾고 삭제한 뒤 “삭제” 표시를 한다.
Open Addressing의 3가지 충돌 처리기법
선형탐사(Linear Probing)

- 선형 탐사는 바로 인접한 인덱스에 데이터를 삽입해가기 때문에 데이터가 밀집되는 클러스터링(Clustering) 문제가 발생하고 이로 인해 탐색, 삭제가 느려진다.
제곱탐사(Quadratic Probing)
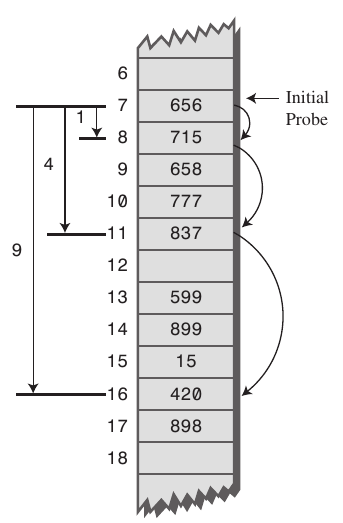
- 1², 2², 3², ... 탐사를 하는 방식으로 선형탐사에 비해 더 폭넓게 탐사하기 때문에 탐색과 삭제에 효율적이다. 그러나 초기 해시 값이 같을 경우 클러스터링 문제가 발생한다.
이중해싱(Double Hashing)
- 선형탐사와 제곱탐사에서 발생하는 클러스터링 문제를 모두 피하기 위해 도입된 것
- 처음 해시 함수로는 해시 값을 찾기 위해 사용
- 두 번째 해시 함수는 충돌이 발생했을 때 탐사 폭을 계산하기 위해 사용
비교
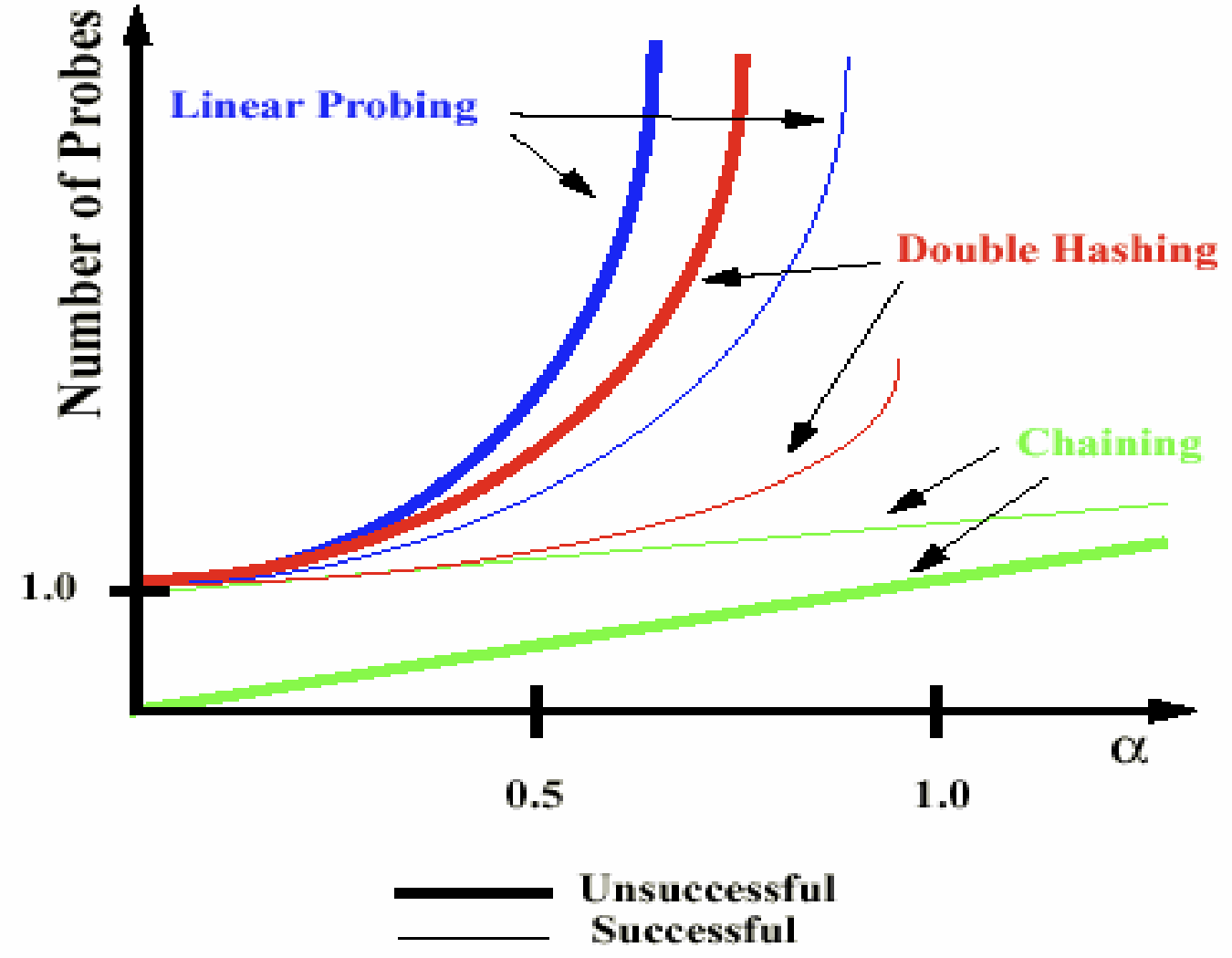
- successful search는 찾고자 하는 데이터가 해시테이블에 있는 경우, unsuccessful search는 없는 경우
체이닝(Chaining)

- 충돌 시 하나의 공간 밖에 없어 이전의 결과가 지워지는 불상사를 막기 위해 충돌하더라도 해당 값을 저장하는 방식
- 충돌이 발생했을 때 이를 동일한 버킷(Bucket)에 저장하는데 이를 연결리스트 형태로 저장하는 방법
- 정해진 해시 테이블 이외의 주소를 추가로 할당해서 확장해서 사용할 수 있다.
시간 복잡도
- 삽입: 연결 리스트에 추가하기만 하면 되므로 상수 시간인 O(1)이 걸린다.
- 탐색, 삭제: 최악의 경우 키 값의 개수인 K에 대해 O(K)가 걸린다. 그러나 최악의 경우보다는 적재율을 이용해서 평균으로 표현하는 것이 일반적이다.
적재율이 α이면 시간 복잡도는 O(α + 1)이다.
뻐꾸기 해싱(Cuckoo Hashing)
- 이론적으로 완벽한 해싱 기법, 최악의 상황에서도 O(1)의 시간 복잡도 구현 가능
- 크기가 같은 2개의 해시 테이블을 사용하고 각각의 해시 테이블은 다른 해시 함수를 가지게 한다.
- 모든 원소는 두 해시 테이블 중 하나에만 있을 수 있으며 그 위치는 해당 해시 테이블의 해시 함수에 의해 결정된다.
-> 즉, 원소가 두 해시 테이블 중 어디든 저장 가능하고 원소가 나중에 다른 위치로 이동 가능
나눗셈법(Division Method)
- 해시 테이블의 크기인 N을 아는 경우 사용 가능
- 해시함수를 적용하고자 하는 값을 N으로 나눈 나머지를 해시값으로 사용하는 방법
-
h(k)=k mod N
-
N은 2의 제곱을 사용하면 안 된다. 2ⁿ로 나타날 때 k의 하위 n개의 비트를 고려하지 않는다. 따라서 N은 소수를 사용하는 것이 좋다.
곱셈법(Multiplication Method)
-
0<A<1인 A 에 대해서 다음과 같이 구할 수 있다.
-
h(k) = ⌊N(kA mod 1)⌋
-
kA mod 1 의 의미는 kA 의 소수점 이하 부분을 말하며 이를 N에 곱하므로 0부터 N사이의 값이 된다. 이 방법의 장점은 N이 어떤 값이더라도 잘 동작한다는 것이며 A 를 잘 잡는 것이 중요하다.
참고 사이트
https://yjshin.tistory.com/369
https://twpower.github.io/139-hash-table-implementation-in-cpp
https://baeharam.netlify.app/posts/data%20structure/hash-table

