재귀함수(Recursion Function)란?

• 함수 내부에서 자기 자신을 호출하는 함수를 의미합니다. 이를 통해서 함수가 자신을 반복적으로 호출하면서 원하는 결과를 도출할 수 있습니다.
• 단, 재귀함수를 사용하는 경우 함수 호출이 계속해서 쌓이기 때문에 호출 스택이 많아져서 성능이 저하될 수 있습니다. 따라서 재귀함수를 작성할 때에는 무한루프에 빠지지 않도록 종료 조건을 명확하게 설정해주어야 합니다.

호출 스택 (Call Stack)이란?

• 프로그램에서 함수나 메서드를 호출할 때 해당 함수나 메서드의 실행이 끝날 때까지 실행되는 다른 함수나 메서드의 호출 정보를 저장하는 자료구조입니다.
• 이 스택은 함수가 호출될 때마다 그 함수의 호출 정보를 저장하고 함수의 실행 결과가 반환되면 해당 함수의 호출 정보를 스택에서 제거합니다.
• 호출 스택은 디버깅, 예외 처리 및 재귀 함수와 같은 다양한 프로그래밍 작업에 사용됩니다.

---

재귀함수의 장단점

1. 장점

• 코드의 가독성이 높아집니다. 재귀적인 호출을 통해 코드르 간결하게 작성할 수 있습니다.
• 일부 알고리즘에서는 반복문을 사용하는 것보다 재귀 함수를 사용하는 것이 더 직관적입니다.
• 변수의 사용을 줄여줍니다. 많은 변수 사용으로 인한 생각지 못한 오류를 줄여줍니다.

2. 단점

• 재귀함수는 함수를 호출할 때마다 스택에 새로운 프레임을 생성합니다. 따라서, 스택이 너무 깊어질 경우(너무 많이 재귀를 호출할 경우)에는 스택오버플로우(Stack Overflow)가 발생할 수 있습니다.
• 재귀함수는 함수의 호출이 반복적으로 일어나기 때문에 ,일반적으로 반복문을 사용하는 것보다 느립니다.

---

재귀함수의 활용 예시

1. 팩토리얼 계산법

public class Factorial {
	public static void main(String[] args) {
		System.out.println(factorial(5));
	}
	public static int factorial(int n){
		if (n==0){ // 기본 케이스
			return 1;
		} else { // 재귀 케이스
			return n*factorial(n-1);
		}
	}
    
	// return 에 대한 설명 :
	// factorial(5) = 5 * factorial(4)
	// factorial(4) = 4 * factorial(3)
	// factorial(3) = 3 * factorial(2)
	// factorial(2) = 2 * factorial(1)
	// factorial(1) = 1 * factorial(0)
	// factorial(0) = 1
	// 따라서 결과값 : factorial(5)는 5 * 4 * 3 * 2 * 1 * 1 = 120

}

2. N 자연수의 합 계산 방법

public class SumOfNaturalNumbers {
	public static void main(String[] args) {
		System.out.println(sumOfNaturalNumber(5));
	}
	static int sumOfNaturalNumber(int n){
		if (n==1){
			return 1;
		} else {
			return n+sumOfNaturalNumber(n-1);
		}
	}
}

3. 거듭제곱(pow) 계산

아래 코드는 Math.pow(2,5); 와 동일한 값을 갖는다.

public class Power {
	public static void main(String[] args) {
		System.out.println(power(2, 5)); // 15
	}

	public static int power(int base, int exponent) {
		if (exponent == 0) {
			return 1;
		} else {
			return base * power(base, exponent - 1);
		}
	}
}

4. 문자열 뒤집기

재귀를 불러내는 자체가 호출 스택이다. 즉, 스택 구조로 자료가 쌓인다.
여기서도 뽑아낸 글자가 스택처럼 쌓인다. 결과적으로 마지막에 출력할때에 스택 구조로 인해서 글자가 거꾸로 생성된다.

public class ReverseString {
	public static void main(String[] args) {
		System.out.println(reverseString("hello")); // "olleh"
	}
	public static String reverseString(String str){
		if (str.length()==0){
			return str;
		} else {
			return reverseString(str.substring(1)) + str.charAt(0);
		}
	}
}

---

재귀함수를 이용한 알고리즘

1. 피보나치 수열 : 경우의 수 계산

피보나치 수열이란 ?

• 이전 두 항의 합이 다음 항이 되는 수열을 의미합니다. 즉, 첫째 항과 둘째 항이 1이고 이후 모든 항은 바로 앞 두항의 합으로 이루어지는 수열을 의미합니다.
• 피보나치 수열의 예로는 [1,1,2,3,5,8,13,21,34,...] 와 같은 형태로 구성됩니다.

public class Fibonacci {

	public static void main(String[] args) {
		int n = 10;
		for (int i = 0; i < n; i++) { // 피보나치 수열 출력
			System.out.println(fibonacci(i) + " ");
		}
	}

	// 피보나치 수열의 결과를 구하는 메서드...
	public static int fibonacci(int n) {
		if (n == 0) {
			return 0;
		} else if (n == 1) {
			return 1;
		} else {
			return fibonacci(n - 1) + fibonacci(n - 2);
		}
	}
}

java 메서드 돌아가는게 정리가 안돼서 직접 적어봤다...

2. 유클리드 호제법 알고리즘 : 최대공약수 계산

유클리드 호제법/알고리즘(Euclidean Algorithm) 이란?

• 두 수의 "최대공약수(GCD)"를 찾기 위한 알고리즘을 의미합니다.
• 큰 수를 작은 수로 나누어 떨어지게 하여 수를 반복적으로 취하여 나머지가 0이 될때까지 작동하는 방법입니다. 이때 가장 작은 수가 최대공약수 입니다.
• 예시로 78696과 19332 의 최대공약수를 구해봅시다.
  

public class EnclideanAlgorithm {

	public static void main(String[] args) {
		int m = 78696;
		int n = 19332;

		System.out.println(gcd(m, n));
	}

	public static int gcd(int m, int n) {
		if (n == 0) {
			return m;
		} else {
			return gcd(n, m % n);
		}
	}
}

3. 이진 탐색(Binary Search) 알고리즘

이진 탐색(Binary Search) 알고리즘이란?

• 정렬된 배열에서 원하는 데이터를 빠르게 찾기 위한 알고리즘 입니다.
• 이진탐색은 배열의 중간값을 선택한 수, 찾고자 하는 데이터와 중간값을 비교합니다. 만약 찾고자 하는 값이 중간값보다 크다면, 중간값의 오른쪽 부분 배열에서 다시 중간값을 선택하여 비교합니다. 반대로 찾고자하는 값이 중간값보다 작다면, 중간값의 왼쪽부분 배열에서 다시 중간값을 선택하여 비교합니다. 이렇게 반복하여 원하는 값을 찾습니다.
• 이진탐색은 데이터의 개수가 많을 때도 빠르게 데이터를 찾을 수 있기 때문에 많이 사용되는 알고리즘 중 하나입니다.
• 이진 탐색은 시간 복잡도가 O(log n)으로, 대규모 데이터에서 매우 효율적인 탐색 방법입니다. 단, 이진 탐색을 사용하기 위해서는 배열이 정렬되어 있어야 합니다.

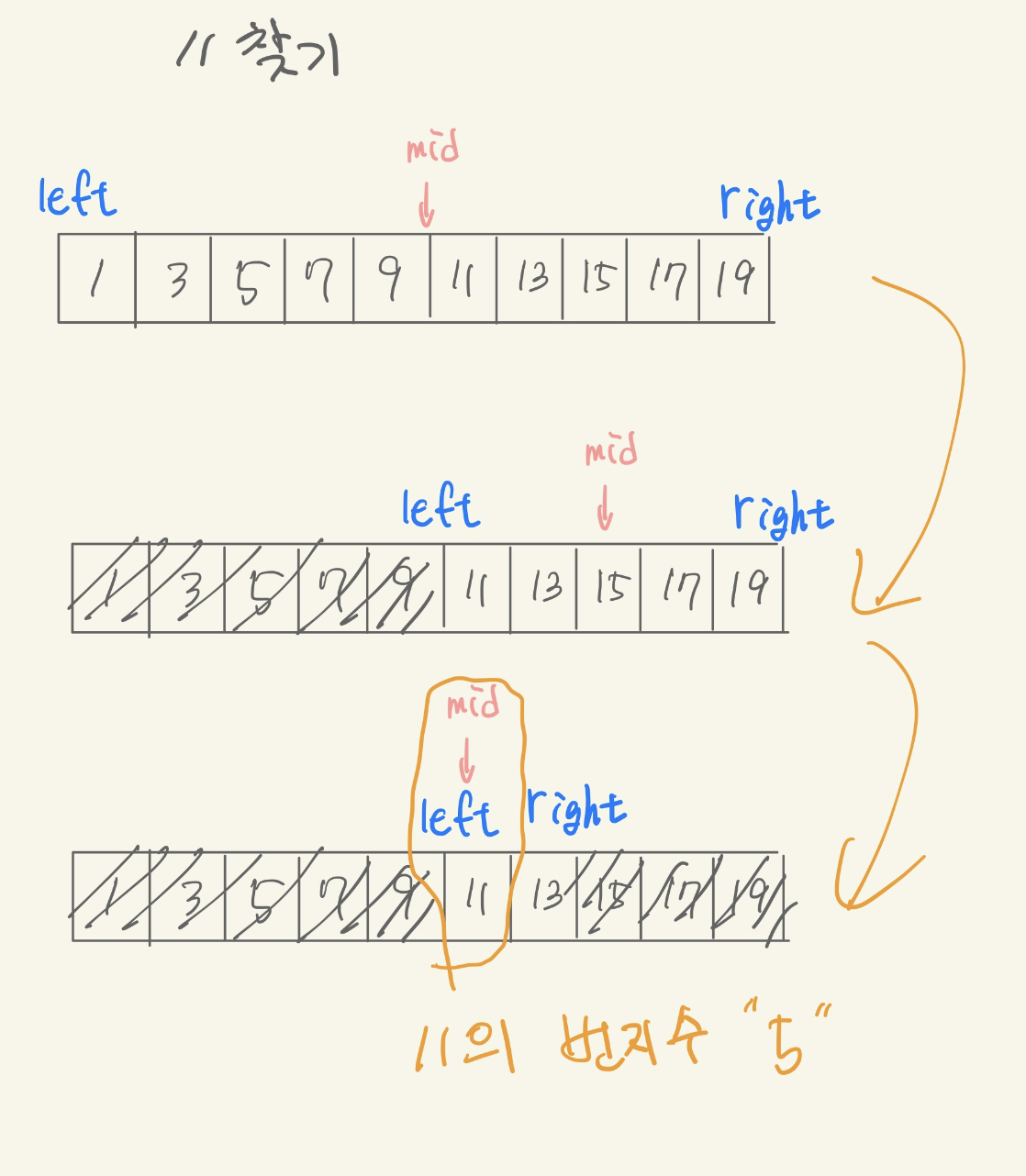
public class BinarySearch {

	static int binarySearch(int[] arr, int target) {
		int left = 0;
		int right = arr.length - 1;

		while (left <= right) {
			int mid = left + (right - left) / 2;

			if (arr[mid] == target) {
				return mid; // 타겟을 찾았을 때 해당 인덱스 반환
			}

			if (arr[mid] < target) {
				left = mid + 1; // 중간값보다 타겟이 크면, 왼쪽 범위를 제외
			} else {
				right = mid - 1; // 중간값보다 타겟이 작으면, 오른쪽 범위를 제외
			}
		}

		return -1; // 타겟이 배열에 없을 경우 -1 반환
	}

	public static void main(String[] args) {
		int[] arr = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19};
		int target = 11;

		int result = binarySearch(arr, target);

		if (result != -1) {
			System.out.println("Element found at index: " + result);
		} else {
			System.out.println("Element not found in the array.");
		}
	}
}