[Leetcode] 1971. Find if Path Exists in Graph

📄 Description

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [${u_i}$, ${v_i}$] denotes a bi-directional edge between vertex ${u_i}$ and vertex ${v_i}$. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex source to vertex destination.

Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.

Example 1:

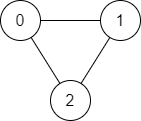
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

Example 2:

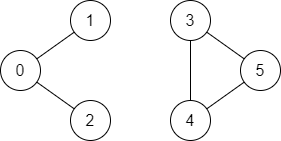
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

Constraints:

• $1 <= n <= {2 * 10^5}$
• $0 <= edges.length <= {2 * 10^5}$
• edges[i].length == 2
• $0 <= {u_i}, {v_i} <= n - 1$
• ${u_i} != {v_i}$
• 0 <= source, destination <= n - 1
• There are no duplicate edges.
• There are no self edges.

💻 My Submission

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        graph=defaultdict(list)
        # make graph
        for n1, n2 in edges:
            graph[n1].append(n2)
            graph[n2].append(n1)
        
        visited=[]
        route=set([source])
        while route:
            node=route.pop()
            if node==destination:
                return True
            # mark visited node
            visited.append(node)
            for d in graph[node]:
                if d not in visited:
                    route.add(d)
        return False

🎈 Better Clean Code-DFS

class Solution:
    def validPath(self, n: int, edges: List[List[int]], start: int, end: int) -> bool:
        neighbors = defaultdict(list)
        for n1, n2 in edges:
            neighbors[n1].append(n2)
            neighbors[n2].append(n1)
            
        def dfs(node, end, seen):
            if node == end:
                return True
            if node in seen:
                return False
            
            seen.add(node)
            for n in neighbors[node]:
                if dfs(n, end, seen):
                    return True
                
            return False
        
        seen = set()    
        return dfs(start, end, seen)

🎈 Better Clean Code-BFS

class Solution:
    def validPath(self, n: int, edges: List[List[int]], start: int, end: int) -> bool:
        neighbors = defaultdict(list)
        for n1, n2 in edges:
            neighbors[n1].append(n2)
            neighbors[n2].append(n1)

        q = deque([start])
        seen = set([start])
        while q:
            node = q.popleft()            
            if node == end:
                return True            
            for n in neighbors[node]:
                if n not in seen:
                    seen.add(n)
                    q.append(n)

        return False

References

• https://leetcode.com/problems/find-if-path-exists-in-graph/
• https://leetcode.com/problems/find-if-path-exists-in-graph/discuss/1449186/Python-DFS-BFS