[Leetcode]1254. Number of Closed Islands

📄 Description

Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

Example 1:

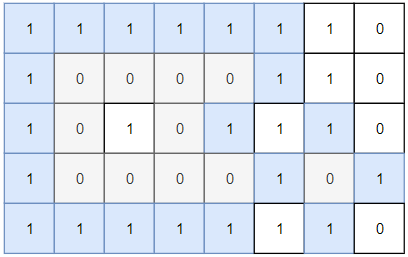
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

Example 2:

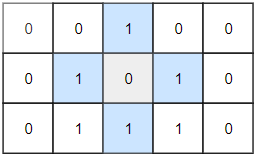
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

Constraints:

• 1 <= grid.length, grid[0].length <= 100
• 0 <= grid[i][j] <=1

💻 My Submission

class Solution:
    def closedIsland(self, grid: List[List[int]]) -> int:
        m, n=len(grid), len(grid[0])
        island=0
        visited=set()

        def dfs(i,j):
            # if it is island on the edge
            if i<0 or j<0 or i>=m or j>=n:
                return 0
            # if it is visited cell or it is not an island
            if grid[i][j]==1 or (i,j) in visited:
                return 1
            visited.add((i,j))
            t=dfs(i+1,j)
            b=dfs(i-1,j)
            l=dfs(i,j-1)
            r=dfs(i,j+1)
            return t and b and l and r
        
                
        for i in range(m):
            for j in range(n):
                # if cell is island
                if grid[i][j]==0 and (i,j) not in visited: 
                    check=dfs(i,j)
                    # if it is closed island
                    if check:
                        island+=1
        return island

👉 Why I was keep failing

My last line of DFS function was like this.

return dfs(i+1,j) and dfs(i-1,j) dfs(i,j-1) dfs(i,j+1)

And I was keep failing with the test case, and I couldn't find why..

Finally I found why it should be like below.

            t=dfs(i+1,j)
            b=dfs(i-1,j)
            l=dfs(i,j-1)
            r=dfs(i,j+1)
            return t and b and l and r

You have to do this instead of return dfs(...) and dfs(...), because you shall let each dfs finish and clean the 0 to 1, for the non closed islands, otherwise it will count more than it should in some cases.

References

• https://leetcode.com/problems/number-of-closed-islands/
• https://leetcode.com/problems/number-of-closed-islands/discuss/425122/Python-easy-understand-DFS-solution