[Leetcode]209. Minimum Size Subarray Sum

📄 Description

Given an array of positive integers nums and a positive integer target, return the minimal length of a contiguous subarray $[nums_{l}, nums_{l+1}, ..., nums_{r-1}, nums_{r}]$ of which the sum is greater than or equal to target. If there is no such subarray, return 0 instead.

Example 1:

Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.

Example 2:

Input: target = 4, nums = [1,4,4]
Output: 1

Example 3:

Input: target = 11, nums = [1,1,1,1,1,1,1,1]
Output: 0

Constraints:

• 1 <= target <= 109
• 1 <= nums.length <= 105
• 1 <= nums[i] <= 105

🎈 Follow up:

If you have figured out the O(n) solution, try coding another solution of which the time complexity is O(n log(n)).

🔨 Several Tries

1. Find the max(nums) and divde it to the left and right part that includes max(nums). Then find the minimum length of subarray in both part and return the smaller one.

   💭 What was the problem?

   There is no guarantee that the max() value will be included in the minimum size subarray.

   For example

   # target=10  
   nums=[5,5,1,1,7,1,1]

   The right subarray should be [5,5] but through above approach, it will return [1,1,7].

🔨 My Solution

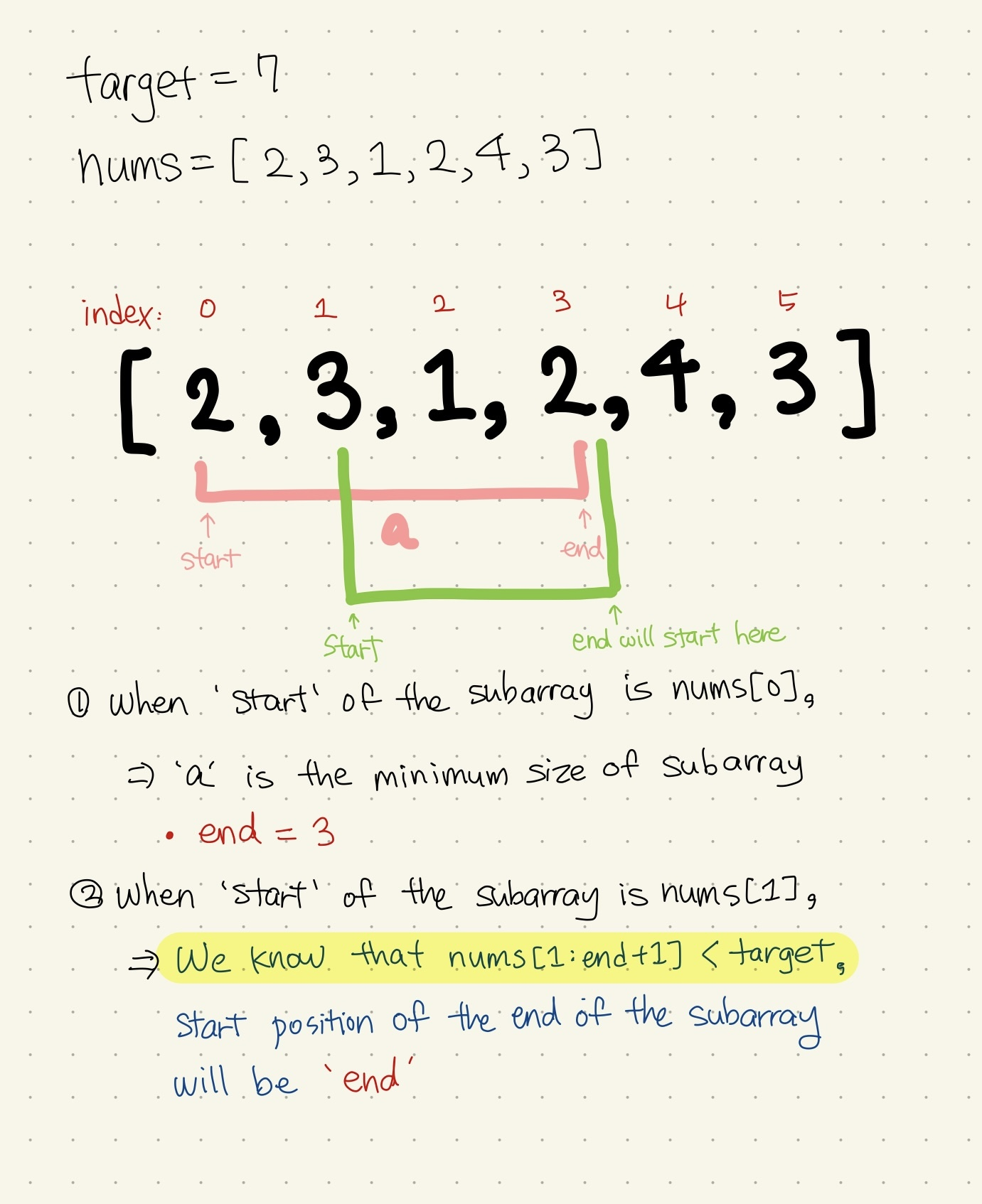
💻 My Submission

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        min_end=0
        min_len=len(nums)
        w_sum=nums[0]
        
        if sum(nums)<target: return 0
        if nums[-1]>=target: return 1
        
        for i in range(len(nums)-1):
            if i>0:
                w_sum-=nums[i-1]
            if i>min_end: 
                min_end=i
            
            # find the min subarray
            while min_end<len(nums):
                if w_sum<target:
                    min_end+=1
                    if min_end==len(nums):break
                    w_sum+=nums[min_end]
                if w_sum>=target:
                    min_len=min(min_len,min_end-i+1)                    
                    break
            # print("-------------")
        return min_len

🕐 Complexity

Time Complexity: O(N)
The worst case is when the minumum subarry is nums array itself.
Space Complexity: O(1)

💡 Other Better Solutions

1. O(N) Appraoach

class Solution:

def minSubArrayLen(self, s, nums):
    total = left = 0
    result = len(nums) + 1
    for right, n in enumerate(nums):
        total += n
        while total >= s:
            result = min(result, right - left + 1)
            total -= nums[left]
            left += 1
    return result if result <= len(nums) else 0

What is different?

1. Nested Loop

• My code: outer loop is for left and inner loop is for `right
• Better solution: outer loop is for right and inner loop is for left

2. Default value for min_len

2. O(NlogN) Approach

class Solution:

def minSubArrayLen(self, target, nums):
    result = len(nums) + 1
    for idx, n in enumerate(nums[1:], 1):
        nums[idx] = nums[idx - 1] + n
    left = 0
    for right, n in enumerate(nums):
        if n >= target:
            left = self.find_left(left, right, nums, target, n)
            result = min(result, right - left + 1)
    return result if result <= len(nums) else 0

def find_left(self, left, right, nums, target, n):
    while left < right:
        mid = (left + right) // 2
        if n - nums[mid] >= target:
            left = mid + 1
        else:
            right = mid
    return left

References

• https://leetcode.com/problems/minimum-size-subarray-sum/
• https://leetcode.com/problems/minimum-size-subarray-sum/discuss/59093/Python-O(n)-and-O(n-log-n)-solution