[프로그래머스] 배달 - 다익스트라

📄 문제 설명

N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.

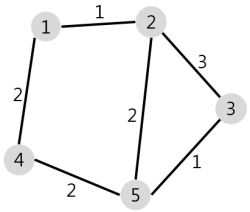
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.

📌 제한사항

• 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
• road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
• road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
• road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
• a, b (1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c (1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는데 걸리는 시간입니다.
• 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
• 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다.
• K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
• 임의의 두 마을간에 항상 이동 가능한 경로가 존재합니다.
• 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.

💻 문제 해결

from collections import defaultdict
import heapq

def solution(N, road, K):
    graph=defaultdict(list)
    # 마을 간 이동 가능 경로 맵 만들기
    for n1,n2,t in road:
        graph[n1].append((n2,t))
        graph[n2].append((n1,t))
	# 마을 별로 배달 가능한 최소 시간        
    dist={n:float('INF') for n in graph}    
    # 1번 마을은 0시간
    dist[1]=0
    
    # 다익스트라 알고리즘
    stack=[]
    heapq.heappush(stack,(1,0))
    while stack:
        vill,time=heapq.heappop(stack)
        if dist[vill]<time:
            continue
        for neigh,t in graph[vill]:
            new_time=t+time
            if dist[neigh]>new_time:
                dist[neigh]=new_time
                heapq.heappush(stack,(neigh,new_time))

    return len([v for v in dist if dist[v]<=K])

💡 기본적인 다익스트라 알고리즘

import heapq  

def dijkstra(graph, start):
  distances = {node: float('inf') for node in graph}  # start로 부터의 거리 값을 저장
  distances[start] = 0  # 시작 값은 0
  queue = []
  heapq.heappush(queue, [distances[start], start])  # 시작 노드부터 탐색 시작 하기 위함.

  while queue: 
    cur_dist, cur_dest = heapq.heappop(queue)  # 탐색 할 노드, 거리를 pop

    if distances[cur_dest] < cur_dist:  # 기존에 있는 거리와 비교
      continue
    
    for new_dest, new_dist in graph[cur_dest].items():
      distance = cur_dist + new_dist  
      if distance < distances[new_dest]:  #  기존 거리보다 작으면 갱신
        distances[new_dest = distance
        heapq.heappush(queue, [distance, new_dest])  
    
  return distances

https://justkode.kr/algorithm/python-dijkstra
https://school.programmers.co.kr/learn/courses/30/lessons/12978