여기를 클릭하면 문제를 볼 수 있습니다.
📕 문제 설명

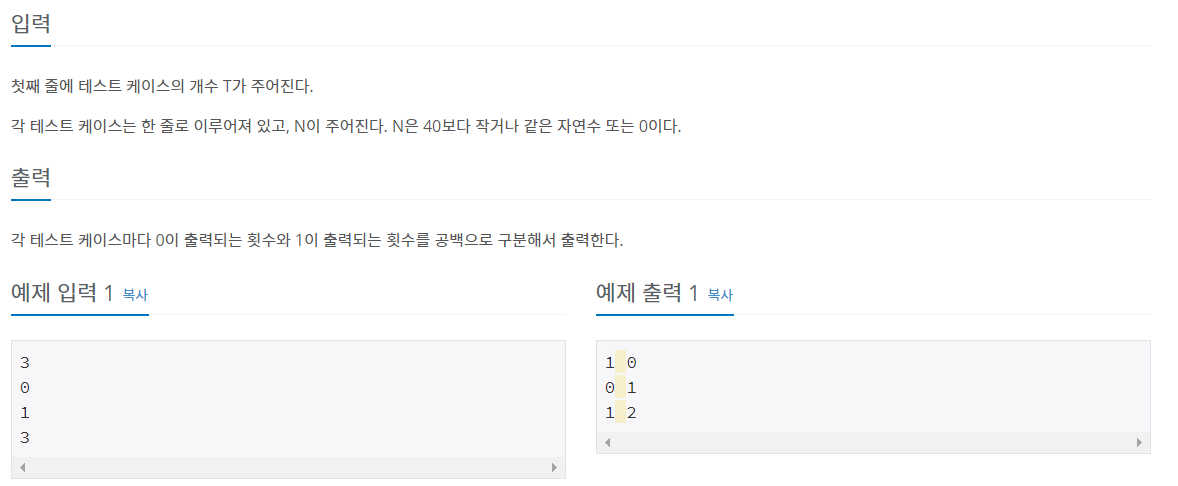
📕 문제 풀이
본 문제는 주어진 재귀함수를 사용하여 풀 수 있습니다.
하지만 주어진 함수를 그대로 사용할 경우 중복되는 연산이 있으므로 불필요한 시간이 소요됩니다.
fibonacci(5)로 예를 들어보겠습니다.
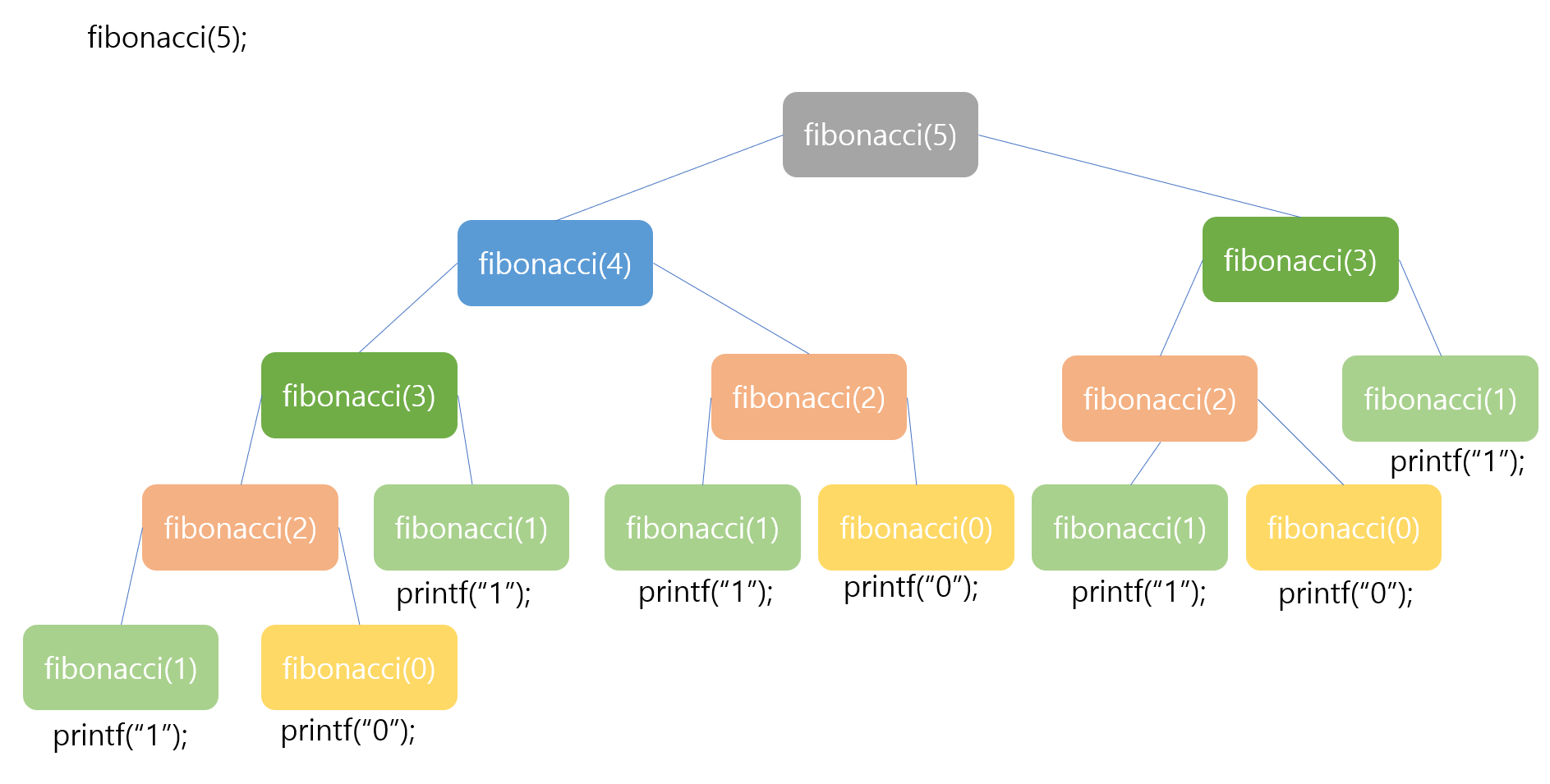
위 이미지는 fibonacci(5); 를 하였을 때 호출하는 함수의 흐름을 간단하게 도식화 한 것 입니다.
살펴보면 재귀적 특성 때문에 동일한 연산을 하는 fibonacci(0), fibonacci(1), fibonacci(2), fibonacci(3)이 여러번 호출되는 것을 볼 수 있습니다.
위에서도 언급했다시피 재귀의 특성에 의해 동일한 연산을 하는 함수를 여러 번 호출 하는 것은 불필요한 시간이 소요됩니다.
그러므로 불필요한 시간 소요를 줄이기 위해서는 동일한 연산을 하는 함수를 여러 번 호출하지 않아야 합니다. 그렇다면 어떻게 해야 한 번만 호출할 수 있을까요?
그것은 바로 정보를 기록하는 것입니다! fibonacci(0) 과 fibonacci(1)이 호출되었을 때 0과 1을 출력한 횟수를 기록한다면 fibonacci(2) 에서는 굳이 fibonacci(1) 과 fibonacci(0) 을 호출하지 않고서 기록된 정보를 가지고 구할 수 있습니다. 그리고 그것을 또 기록하면 되는 것이죠.
그러면 fibonacci(3) 에서는 fibonacci(2) 와 fibonacci(1) 을 굳이 호출하지 않고 기록된 정보만 가지고 구할 수 있습니다.
이와 같은 방법으로 동일한 연산을 하는 함수를 반복적으로 호출하지 않고도 기록된 정보만 가지고 0과 1의 출력횟수를 구할 수 있게 되었습니다.
이와 같은 방법을 memoization이라고 합니다. memoization은 정보를 기록함으로써 불필요한 연산을 줄이는 방법을 뜻하며 dynamic programming(동적 계획법)의 핵심이 되는 기술입니다.
이제 정보를 기록하는 과정을 자세히 살펴보겠습니다.
이전과 동일하게 fibonacci(5)를 예로 설명하겠습니다.
fibonacci(5)를 호출하면fibonacci(0)부터fibonacci(5)까지 0과 1의 출력횟수를 각각 저장하는 변수가 필요합니다.

- 이제 base인
fibonacci(0)과fibonacci(1)에 출력횟수를 기록합니다.

fibonacci(2)부터는 재귀함수의 특징을 사용하여 출력횟수를 구합니다. 본래의fibonacci(2)는fibonacci(1)+fibonacci(0)입니다. 하지만 이미fibonacci(1)과fibonacci(0)의 출력횟수를 기록하였기 때문에 함수를 호출할 필요 없이 기록된 정보를 더하기만 하면 됩니다.

fibonacci(3)또한fibonacci(2)와 같이 구하면 됩니다.fibonacc(2)의 출력횟수와fibonacci(1)의 출력횟수를 더하면 되는 것이죠.

fibonacci(4)와fibonacci(5)도 동일한 방법으로 구해줍니다.


총 5번의 연산만으로 fibonacci(5)의 0과 1 출력횟수를 구할 수 있게 되었습니다.
만약 memoization을 하지 않고 재귀함수로 구했다면 연산횟수는 15번의 연산이 필요합니다. memoization 덕분에 무려 3배나 연산횟수를 줄일 수 있게 되었네요.
이게 바로 memoization 이 중요한 이유입니다.
이제 이를 코드로 나타내봅시다.
📕 Code
#include <iostream>
using namespace std;
int f[41][2] = {{0, }, }; // 출력횟수를 기록하기 위한 배열
void fibonacci(int n)
{
if (n == 0) // fibonacci(0)일 때는 0의 출력횟수를 기록
f[n][0] = 1;
else if (n == 1) // fibonacci(1)일 때는 1의 출력횟수를 기록
f[n][1] = 1;
else // 그 외에는 fibonacci(n-1)의 출력횟수+fibonacci(n-2)의 출력횟수
{
f[n][0] = f[n-1][0]+f[n-2][0];
f[n][1] = f[n-1][1]+f[n-2][1];
}
}
int main(void)
{
int t;
scanf("%d", &t);
int n;
int j = 0;
for(int i=0; i<t; i++) // 주어진 t만큼
{
scanf("%d", &n); // n을 입력받아
for(; j<=n; j++) // 0부터 n까지 finbonacci() 연산
fibonacci(j);
printf("%d %d\n", f[n][0], f[n][1]); // 출력횟수를 출력!
j = n+1; // t=2, n=3, 5 라면 첫 번째 시행에서 0부터 3까지의 fibonacci()를 수행,
// 그러면 5를 구하기 위해서는 0부터 5까지가 아니라 4부터 5까지만 구하면 됨!
// 그러므로 for문의 시작을 n+1로 해준다.
}
return 0;
}📕 후기
요시, 다이나믹 프로그래밍 시즌!🏏
