[백준] 9663번: N-Queen

여기를 클릭하면 문제를 볼 수 있습니다.

📕 문제 설명

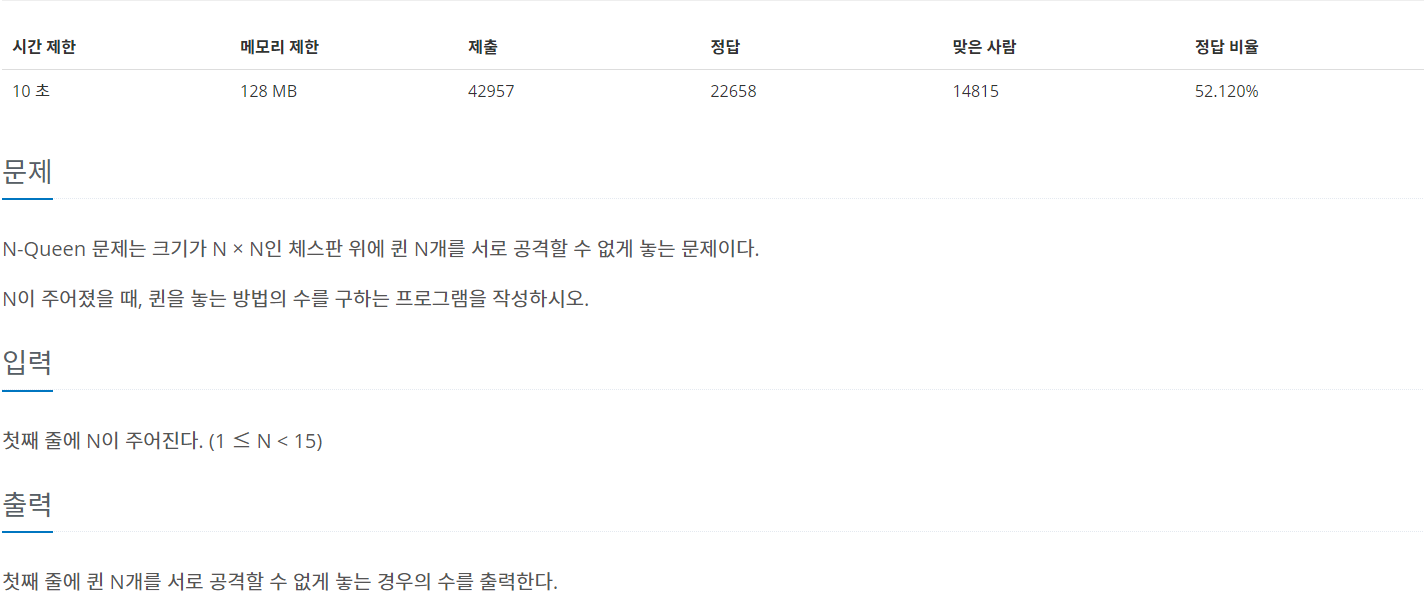
이미지에 적혀있는대로 N이 주어졌을 때 N*N 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력하는 문제이다.
퀸은 퀸이 위치한 행, 열, 대각선으로 이동이 가능하다. (사진 참고)

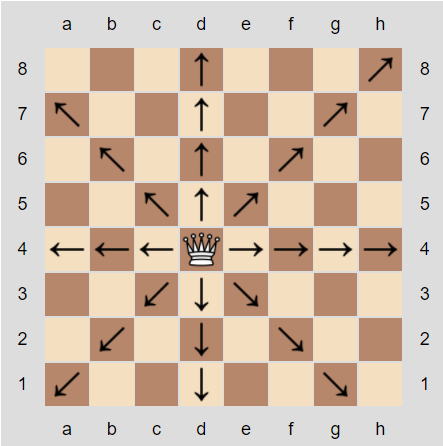
이러한 규칙 하에 N개의 퀸을 서로 공격할 수 없게 배치해야 한다.

📕 문제 풀이

첫째 열, 첫째 행에 퀸을 놓은 다음 둘째 행에 두 번째 퀸을 놓되 크 칸에 퀸을 놓아도 서로 공격할 수 없는지 확인 후 공격할 수 없다면 그 칸에 놓고 반대로 공격할 수 있다면 칸을 한 칸 오른쪽으로 옮겨 다시 검사하고 이런 방식으로 해야하는 문제이다. 즉, 전형적인 backtracking 방식이다.

그러므로 체스판에 퀸이 올려져 있는지 확인하기 위한 배열과
퀸이 서로 공격할 수 없는지 확인하는 함수를 생성하면 된다.

📕 Code

#include <iostream>

using namespace std;

#define MAX		15

bool visited[MAX][MAX] = {{0, }, };
int n;
int cnt = 0;

bool isValid(int y, int x);
void nQueen(int y, int qn);

int main(void)
{
	scanf("%d", &n);
	nQueen(0,0);
	printf("%d ", cnt);

	return 0;
}

bool isValid(int y, int x)
{
	// 가로줄 확인
	for(int i=0; i<n; i++)
		if(visited[y][i])
			return false;
	// 세로줄 확인
	for(int i=0; i<n; i++)
		if(visited[i][x])
			return false;
	// '\' 윗대각선 확인 
	for(int i=y-1, j=x-1; i>=0 && j>=0; i--, j--)
		if(visited[i][j])
			return false;
	// '\' 아랫대각선 확인
	for(int i=y+1, j=x+1; i<n && j<n; i++, j++)
		if(visited[i][j])
			return false;
	// '/' 윗대각선 확인
	for(int i=y-1, j=x+1; i>=0 && j<n; i--, j++)
		if(visited[i][j])
			return false;
	// '/' 아랫대각선 확인
	for(int i=y+1, j=x-1; i<n && j>=0; i++, j--)
		if(visited[i][j])
			return false;
	return true;
}

void nQueen(int y, int qn)
{
	if(qn == n)		// 퀸을 n개 놓았다면 경우의 수++
	{
		cnt++;		
		return;
	}
	for(int i=0; i<n; i++)	// 한 열의 한 칸씩
	{
		if(isValid(y, i))	// 이 칸에 놓아도 N개의 퀸들이 서로 공격할 수 없는가?
		{
			visited[y][i] = 1;	// 그렇다면 놓고
			nQueen(y+1, qn+1);	// 다음 열에 퀸을 놓으러 간다.
			visited[y][i] = 0;	
		}
	}
}

📕 후기

backtracking 알고리즘을 적용한 문제를 처음으로 혼자 풀어 뿌듯했다. backtracking에 대해서 이제 이해가 되기 시작한 것 같다.