
2021-11-18
기본 수학2
소수와 기하를 다뤄 봅시다.
1단계 1978 소수 찾기
문제
주어진 수 N개 중에서 소수가 몇 개인지 찾아서 출력하는 프로그램을 작성하시오.
입력
첫 줄에 수의 개수 N이 주어진다. N은 100이하이다. 다음으로 N개의 수가 주어지는데 수는 1,000 이하의 자연수이다.
출력
주어진 수들 중 소수의 개수를 출력한다.
Java 11
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N;
N = sc.nextInt();
int count=0;
for(int i=0; i<N; i++) {
int A;
A = sc.nextInt();
int tmp = 0;
for(int j=1; j<A; j++) {
if(A%j == 0) {
tmp++;
}
}
if(tmp == 1) {
count++;
}
}
System.out.println(count);
}
}2단계 2581 소수
문제
자연수 M과 N이 주어질 때 M이상 N이하의 자연수 중 소수인 것을 모두 골라 이들 소수의 합과 최솟값을 찾는 프로그램을 작성하시오.
예를 들어 M=60, N=100인 경우 60이상 100이하의 자연수 중 소수는 61, 67, 71, 73, 79, 83, 89, 97 총 8개가 있으므로, 이들 소수의 합은 620이고, 최솟값은 61이 된다.
입력
입력의 첫째 줄에 M이, 둘째 줄에 N이 주어진다.
M과 N은 10,000이하의 자연수이며, M은 N보다 작거나 같다.
출력
M이상 N이하의 자연수 중 소수인 것을 모두 찾아 첫째 줄에 그 합을, 둘째 줄에 그 중 최솟값을 출력한다.
단, M이상 N이하의 자연수 중 소수가 없을 경우는 첫째 줄에 -1을 출력한다.
Java 11
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int M;
M = sc.nextInt();
int N;
N = sc.nextInt();
int sum = 0;
int min = N;
int tmp = 0;
for(int i=M; i<=N; i++) {
tmp = 0;
for(int j=1; j<=i; j++) {
if(i%j == 0)
tmp++;
}
if(tmp == 2) {
sum += i;
if(min>i)
min = i;
}
}
if(sum == 0) {
System.out.println(-1);
} else {
System.out.println(sum);
System.out.println(min);
}
}
}3단계 11653 소인수분해
문제
정수 N이 주어졌을 때, 소인수분해하는 프로그램을 작성하시오.
입력
첫째 줄에 정수 N (1 ≤ N ≤ 10,000,000)이 주어진다.
출력
N의 소인수분해 결과를 한 줄에 하나씩 오름차순으로 출력한다. N이 1인 경우 아무것도 출력하지 않는다.
Java 11
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N;
N = sc.nextInt();
int min = 2;
while(N >= min) {
if(N % min == 0) {
System.out.println(min);
N /= min;
} else {
min++;
}
}
}
}4단계 1929 소수 구하기
문제
M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
출력
한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다.
Java 11
import java.util.*;
public class Main {
public static boolean[] prime;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int M;
M = sc.nextInt();
int N;
N = sc.nextInt();
prime = new boolean[N+1];
get_prime();
for(int i=M; i<=N; i++) {
if(!prime[i]) System.out.println(i);
}
}
private static void get_prime() {
prime[0] = prime[1] = true;
for(int i=2; i<=Math.sqrt(prime.length); i++) {
if(prime[i])
continue;
for(int j=i*i; j<prime.length; j+=i) {
prime[j] = true;
}
}
}
}📝 오늘의 공부 📝
에라토스테네스의 체
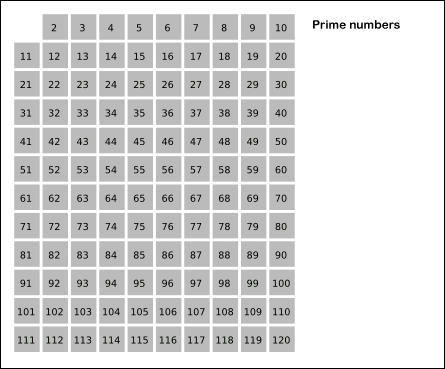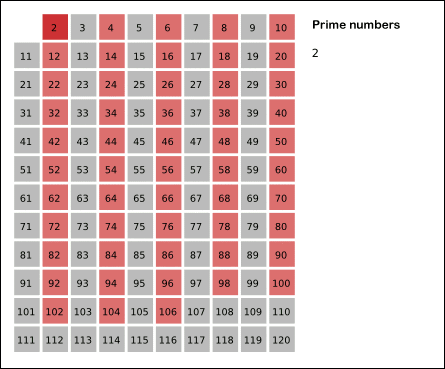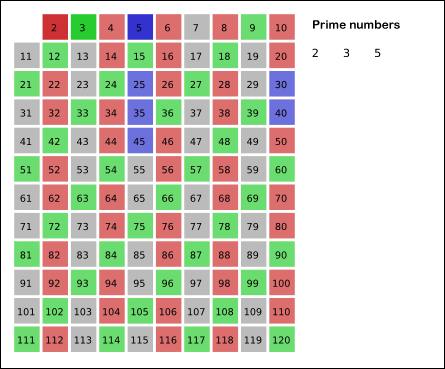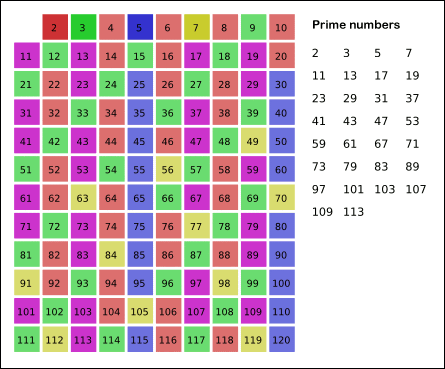
에라토스테네스의 체는 소수가 아닌 수를 지워나가는 것이다.
이 방법으로 소수를 찾으려면, 2부터 시작해 자연수를 차례로 쓴 다음, 2 이외의 2의 배수, 3 이외의 3의 배수, 5 이외의 5의 배수의 순서로 수를 지워나가 끝에 남는 수가 소수이다.
2부터 n까지의 숫자 중에서 에라토스테네스의 체로 소수를 찾으려면, 2부터 시작해 n까지의 자연수를 차례로 쓴다. (2, 3, 4, ..., n)
그리고 2 이외의 2의 배수를 지운다(p=2). 이때 2가 최초의 소수가 된다.
그 다음 소수인 3을 제외한 3의 배수를 지운다(p=3).
이 방법을 다음에 지울 소수, 즉 p의 제곱이 n 보다 커질 때까지, 이 방법을 계속한다(p2≥n).
그러면 체로 친 것처럼 끝에 남는 수가 있다. 이 수가 바로 그 자신과 1 이외의 다른 수로는 나누어 떨어지지 않는 소수이고, 이렇게 소수를 찾는 방법을 에라토스테네스의 체라고 한다. 이 과정은 끝없이 계속되지만 20까지 자연수를 지워나가도 소수가 2, 3, 5, 7, 11, 13, 17, 19임을 쉽게 알 수 있다.
