🌼시간 복잡도
시간 복잡도란 알고리즘을 수행할 때 걸리는 시간을 기준으로 효율성을 분석하는 것이다. 시간의 효율성이란 결국 알고리즘에서 비교와 교환 등이 일어날 때 연산자의 처리 횟수가 적다는 의미이며, 연산자의 처리 횟수가 적다는 건 시간의 복잡도가 낮다는 의미이다. 따라서 시간 복잡도가 낮을수록, 연산자의 사용 횟수가 적을수록 효율성이 높은 알고리즘이 된다. 다만, 시간 복잡도 표기에 있어서 정확한 Running time을 계산하는 목적은 아니므로 상수는 생략한다.
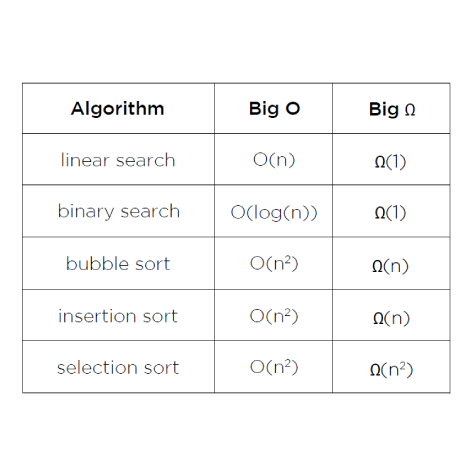
Big-O 표기법:Big-O 표기법은 컴퓨터 과학에서 "대략"을 나타내는 공식적인 개념으로최악의 경우에 대한 시간 복잡도를 나타내는 표현법이다.알고리즘의 성능을 수학적으로 표현해주는 표현법이다. 해당 표기법을 사용하면 알고리즘의 시간, 공간 복잡도를 표현할 수 있다. ex) O(n + n) = O(2n) = O(n)
Q. 버블 정렬의 최악의 경우에서 시간 복잡도는 n^2이다. 이를 증명해보시오.
버블 정렬을 수행하면 n-1부터 1까지 정렬을 반복한다. (n-1) + (n-2) ・ ・ ・ + 1
이것의 합은 등차수열의 합 공식을 사용하면 쉽게 알 수 있다.S = (n-1) + (n-2) ・ ・ ・ + 1 ・・・ 1️⃣
S = 1 + ・ ・ ・ + (n-2) + (n-1) ・・・ 2️⃣ (1의 식을 거꾸로 뒤집은 것)1️⃣, 2️⃣의 좌항, 우항 각각 더해 하나의 식으로 만들면 아래와 같다.
2S = n(n-1) → S = n(n-1) / 2 → S = (n^2 - n)/2
최종 오른쪽 표현식에서 시간복잡도 표기 기준으로 상수를 제거하면 버블 정렬의 Big O는 O(n^2)이 된다.
-
Big-Ω 표기법: : Big-O와 비슷한 Big-Ω (omega) 표기법이 있는데 Big Ω는 최선의 경우를 나타낸다. 버블 정렬에서 최선의 경우(이미 정렬된 배열)를 생각해보면 버블 정렬은 교환이 이루어지지 않더라도 배열이 정렬된 사실을 모르기 때문에 여전히 n-1번의 비교를 해줘야 한다. 그래서 최선의 경우는 Ω(n)로 표기한다. -
Big-Θ 표기법: Big O 와 Big Ω의 공통 부분으로 최소와 최악의 중간인 평균 복잡도를 나타낸다. 예를 들어 Big O 와 Big Ω의 시간 복잡도가 n^2으로 같은 경우에는 ⍬(n^2)로 표기할 수 있다.
🌼Big O 표현법으로 알아보는 시간 복잡도 유형
O(1): 입력 데이터의 크기에 상관없이 언제나 일정한 시간(Constant time)이 걸리는 알고리즘이다.데이터의 크기와 성능이 비례하지 않는다.
function zero(arr) {
return arr[0] === 0 ? true : false;
} O(n): 입력받은 데이터의 크기만큼(Linear time) 수행하는 알고리즘
function print(arr) {
for (let i = 0; i < n; i++) {
console.log(arr[i]);
}
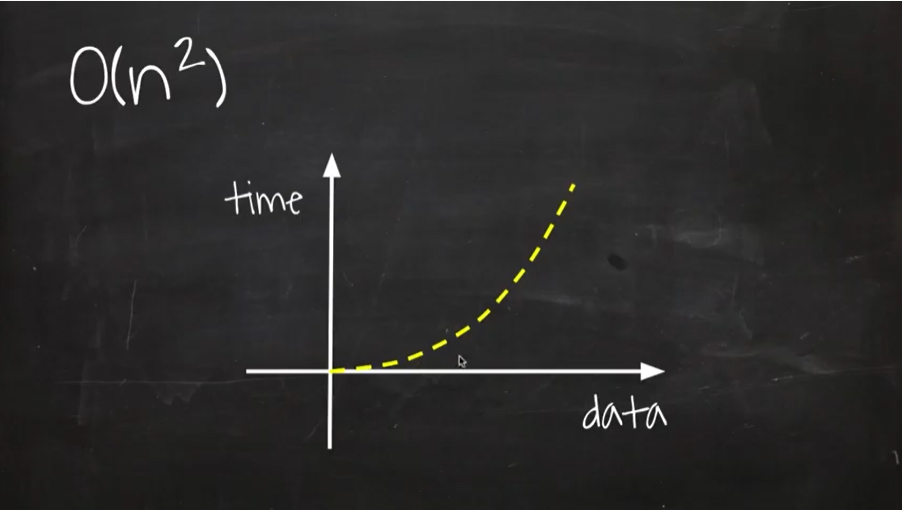
} O(n²): 입력받은 데이터의 크기에 크기만큼 연산하여 값을 출력하는 알고리즘
function square(n) {
for (let i = 1; i <= n; i++) {
for (let j = i; j <=i; j++) {
console.log(i * j);
}
}
}
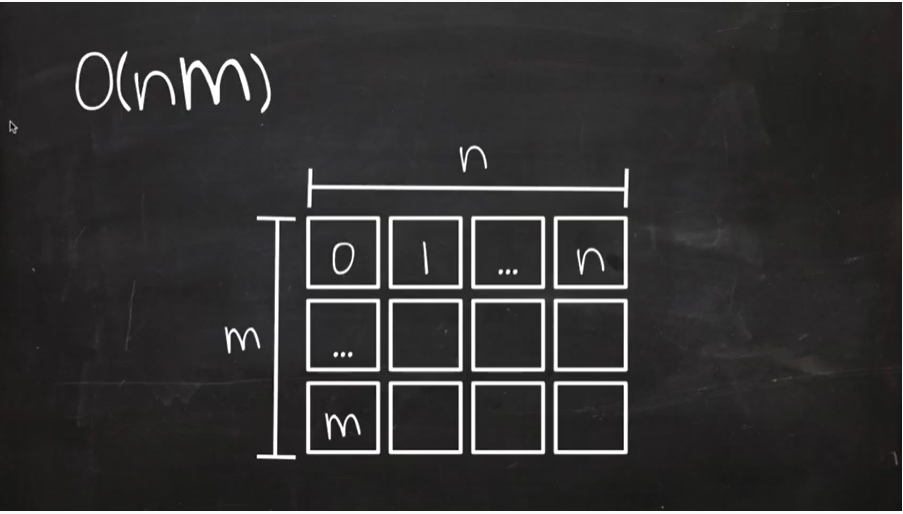
O(nm): 입력받은 값이 2개일 경우, 값의 곱만큼 연산하여 값을 출력하는 알고리즘
function sum(a, b) {
for (let i = 0; i < a; i++) {
for (let j = 0; j < b; j++) {
console.log(i + j);
}
}
}
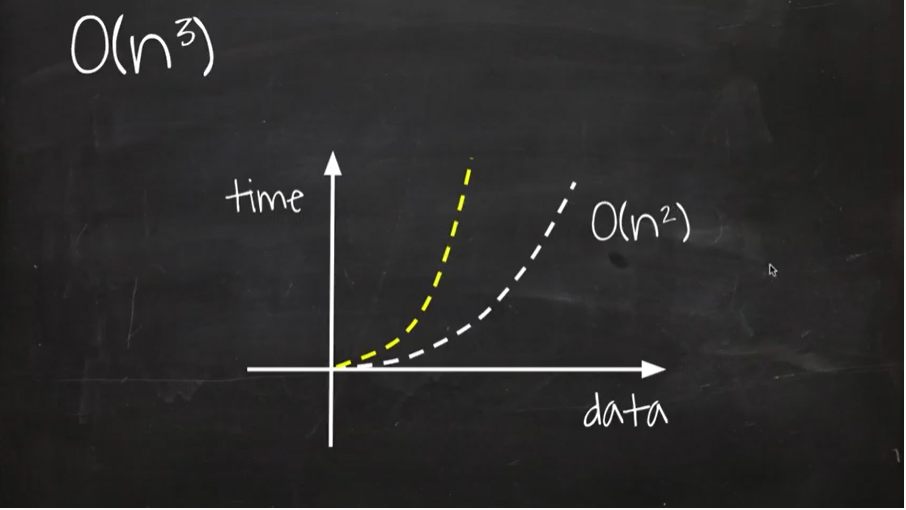
O(n³): 입력받은 데이터의 크기에 크기만큼 연산하여 값을 출력하는 알고리즘
function volume(n) {
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {
for (let k = 1; k <= n; k++) {
console.log(i * j * k);
}
}
}
}
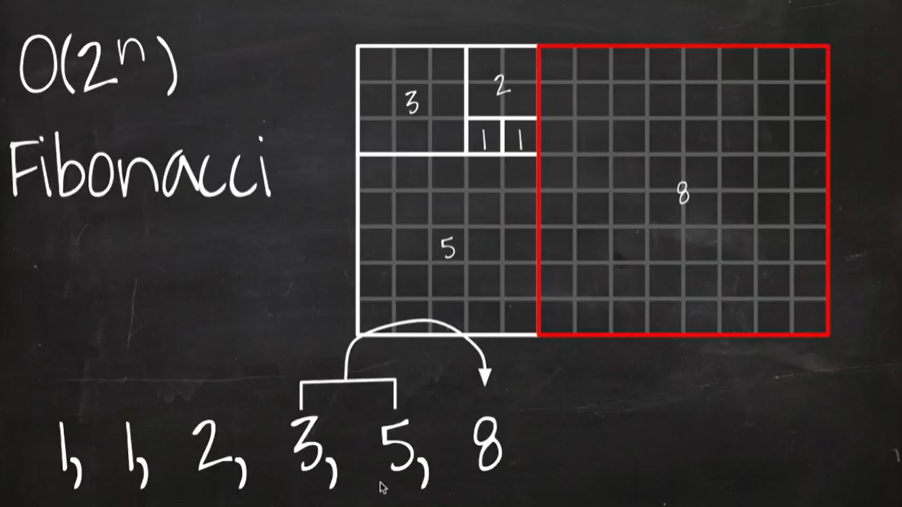
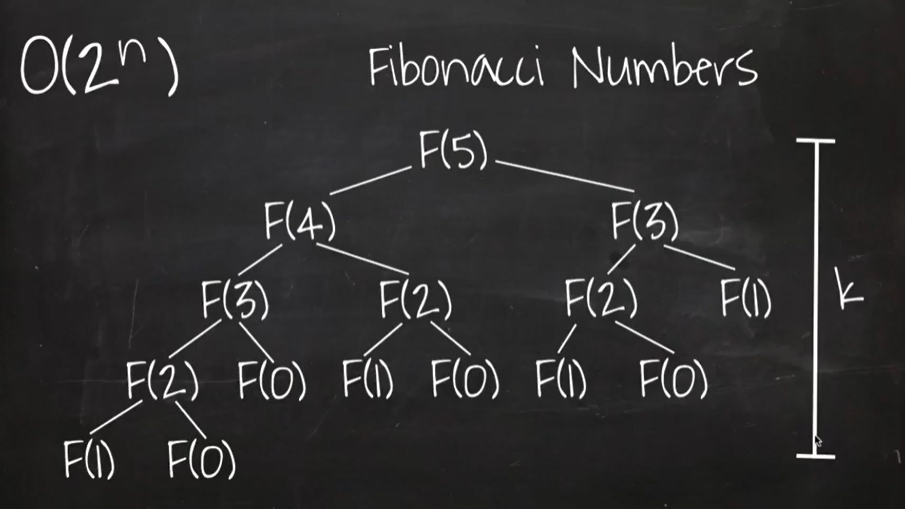
O(2ⁿ): 입력받은 데이터의 길이를 데이터의 크키만큼(Exponential time) 연산하여 값을 출력하는 알고리즘
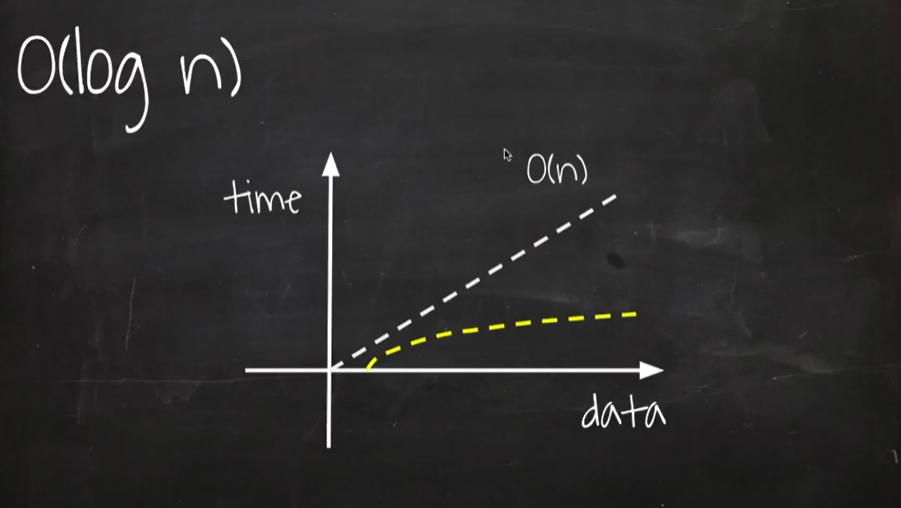
O(log n): 알고리즘을 수행할수록 데이터의 길이의 절반씩 수행횟수가 줄어드는 알고리즘이다.log n의 대표적인 알고리즘으로 Binary search가 있다. Binary search의 전제조건은 데이터가 정렬되어 있어야 한다는 것이다.
O(sqrt(n)): 데이터를 정사각형 구조에 채우고 맨 윗줄만 순회하는 알고리즘
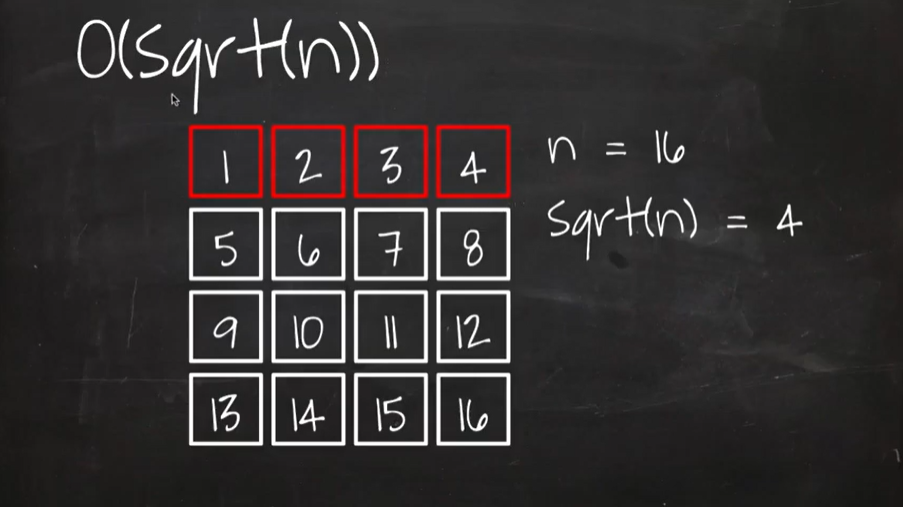
출처: YOUTUBE-엔지니어대한민국, edwith-[해외명강] 컴퓨터 과학 교양 강좌: CS50

