[백준11689]GCD(n,k)=1 (오일러의 피)

https://www.acmicpc.net/problem/11689

입력:첫째 줄에 자연수 n (1 ≤ n ≤ 1012)이 주어진다.

출력:GCD(n, k) = 1을 만족하는 자연수 1 ≤ k ≤ n 의 개수를 출력한다.

풀이

https://ko.wikipedia.org/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC_%ED%94%BC_%ED%95%A8%EC%88%98

오일러의 피 함수를 그대로 구현하면 되는 문제이다.

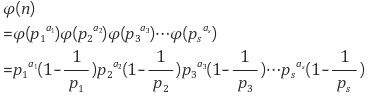
이 식은 곧

answer = answer / i * (answer - 1);

오일러의 피 자체가 에라스토 체와 비슷하다.
n의 제곱근까지만 탐색을하고 자료형은 수가 커 long long이다

코드

#include <iostream>
 
using namespace std;

 
long long oiler(long long n)
{
    long long ret = n;
    long long sqrtn = sqrt(n);
    for (long long i = 2; i <= sqrt(n); div++) {
        if(n%i == 0) {
            ans = ans / ans * (i - 1);
        }
        while(n%i==0) {
            n /= i;
        }
        
    }
    if(n != 1) { 
        ans = ans / n * (n-1);
    }
    return ans;
}
 
int main() {
	long long n
    cin>>n;
    long long  answer = oiler(n);
    cout<<answer;
}