백준 - 골드바흐 파티션(17103)

문제 출처

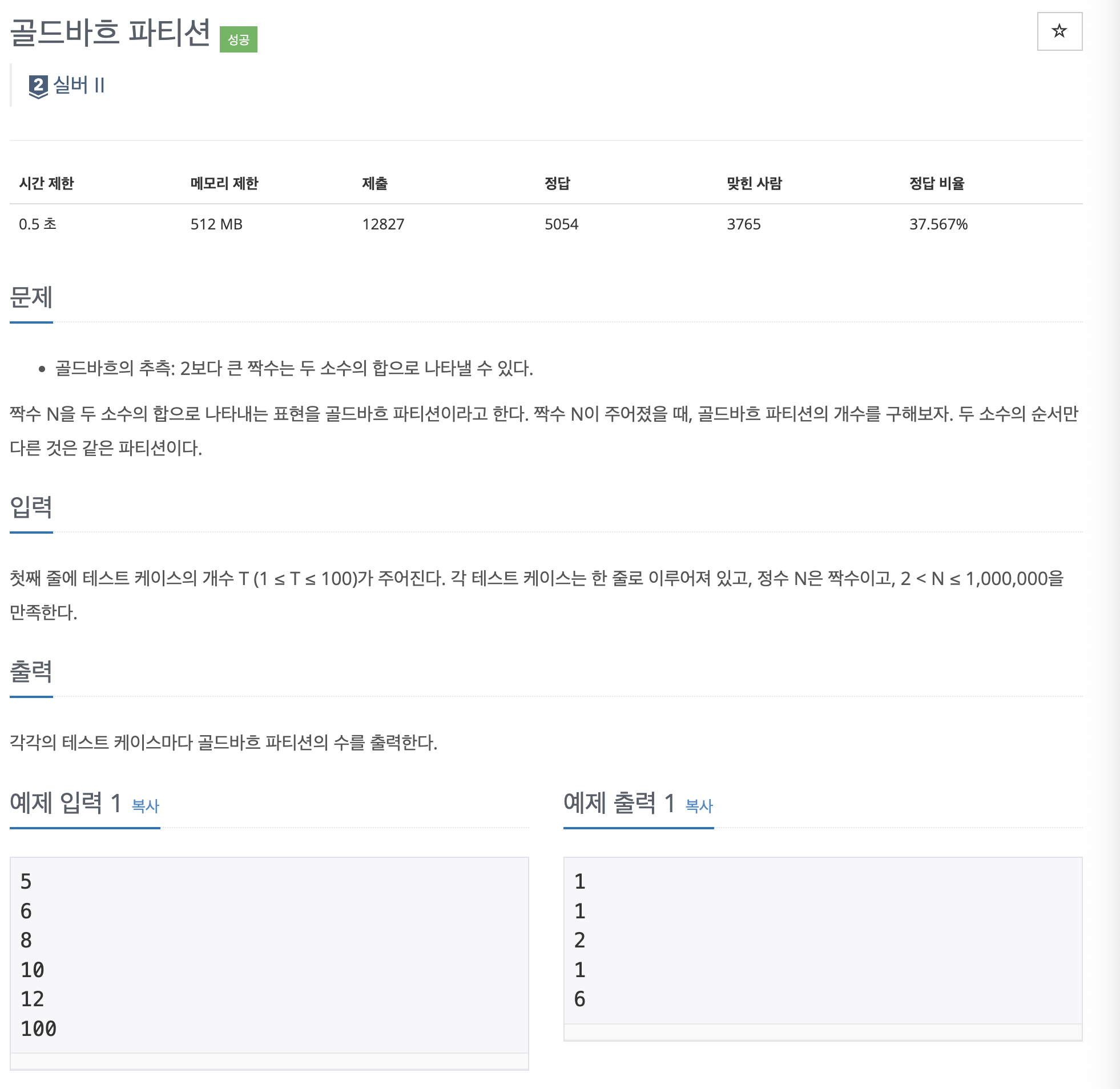
문제 출처 : 골드바흐 파티션

문제 이해하기

짝수 N이 주어졌을 때, 골드바흐 파티션의 개수를 구하는 문제이다. 이때 두 소수의 순서가 달라도 하나의 파티션으로 취급한다.

주요 조건 이해하기 ⭐️

두 소수의 순서가 달라도 하나의 파티션으로 취급한다는 이야기는

8를 예로 들어보면 8 = 3 + 5 = 5 + 3 두 소수의 순서는 다르지만 결과적으로 8이라는 숫자를 만들 수 있는 경우를 하나의 파티션으로 취급한다는 이야기이다.

바로 어떻게 풀지 순서를 나열해보면

1. 입력을 받는다.
2. 에라토스테네스의 체를 만든다.
3. 입력으로 들어온 숫자를 절반으로 나눈다.
4. 절반을 기준으로 left, right 탐색을 한다. (반복)
5. left or right 값이 끝에 도달하면 반복문을 탈출한다.

이 문제는 에라토스테네스의 체와 left, right 기준으로 탐색을 할 수 있으면 큰 어려움 없이 문제를 풀 수 있다.

제출 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {

	static final int MAX_LENGTH = 1_000_001;
	static boolean[] notPrime = new boolean[MAX_LENGTH + 1];
	static StringBuilder sb = new StringBuilder();

	// false = 소수, true = 소수가 아님
	static {
		notPrime[0] = notPrime[1] = true;

		for (int i = 2; i <= MAX_LENGTH; i++) {
			if (notPrime[i]) {
				continue;
			}
			for (int j = i + i; j <= MAX_LENGTH; j += i) {
				notPrime[j] = true;
			}
		}
	}

	// 입력받은 수를 절반으로 나눠 골드바흐 파티션을 구한다.
	private static int findGoldbachPartition(int n) {
		int count = 0;

		int left = n / 2;
		int right = n / 2;

		while (left != 1 && right != n) {
			if (!notPrime[left] && !notPrime[right]) {
				count++;
				left--;
				right++;
			} else {
				left--;
				right++;
			}
		}

		return count;
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int T = Integer.parseInt(br.readLine());
		int[] arr = new int[T];

		for (int i = 0; i < T; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}

		for (int i = 0; i < T; i++) {
			sb.append(findGoldbachPartition(arr[i])).append("\n");
		}
		System.out.println(sb);
	}

}