199. Binary Tree Right Side View

---

문제 분석

이진 트리의 루트가 주어지면 자신이 그 오른쪽에 서 있다고 상상하고 위에서 아래로 정렬된 노드 값을 반환합니다.

---

풀이 과정

depth 가 같은 node 는 마지막에 추가된 node 가 우측에서 볼 수 있는 node 가 된다.

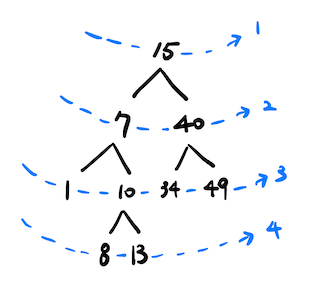
아래와 같은 트리가 있다고 가정한다.
input = [15, 7, 40, 1, 10, 34, 49, null, null, 8, 13]

파란색 글씨 는 level 을 나타낸다.

level 의 특성을 살펴보자면,
root node(15) 의 자식 노드인 left, right 가 두 번째 level 이 된다.
두 번째 level 의 자식들이 세 번째 level 이 된다.
부모의 자식들이 다음 level 이 된다.

위의 특성을 이용하여 문제를 풀려면 Queue 자료 구조 필요하다. (선입선출)
Queue 에 같은 level 의 node 를 모두 추가한다.
Queue 마지막에 추가된 node 가 우측에서 볼 수 있는 node 가 된다.
Queue 에서 node 의 left, right 노드들은 다음 level 의 node 가 된다.

1. 15 를 Queue 에 추가한다. (level = 1)
2. 마지막에 추가된 15 가 우측에서 볼 수 있는 node 가 된다. (level = 1)
3. 15 의 자식 노드인 7, 40 을 Queue 에 추가한다.
4. 마지막에 추가된 40 이 우측에서 볼 수 있는 node 가 된다. (level = 2)
5. 7, 40 의 자식 노드인 1, 10, 34, 49 를 Queue 에 추가한다.
6. 마지막에 추가된 49 가 우측에서 볼 수 있는 node 가 된다. (level = 3)
7. 1, 10, 34, 49 의 자식 노드인 8, 13 을 Queue 에 추가한다.
8. 마지막에 추가된 13 가 우측에서 볼 수 있는 node 가 된다. (level = 4)

(엄연히 따지면 자식 노드는 아니다. 다음 레벨 정도로 이해하자.)

---

나의 생각

좌측에서 바라본다면 첫 번째 값이 될테고, 우측에서 바라본다면 마지막 값이 될테니 이진 트리가 아니더라도 트리 구조이기만 한다면, 그렇게 만들 수 있다면 접근이 가능한 문제 같다.
해당 문제의 요점은 level 로 나누어진 계층을 탐색할 수 있는지 물어보는 문제 같다.

---

코드

class Solution {
 
    public List<Integer> rightSideView(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<Integer> result = new ArrayList<>();

        queue.offer(root);

        while(!queue.isEmpty()) {
            int size = queue.size();
            TreeNode node = null;

            for (int i = 0; i < size; i++) {
                node = queue.poll();
                if (node == null) break;

                TreeNode left = node.left;
                TreeNode right = node.right;

                if (left != null) queue.offer(left);
                if (right != null) queue.offer(right);
            }

            if(node != null) result.add(node.val);
        }

        return result;
    }

}