212. Word Search II

---

문제 분석

2차원 문자 배열과 문자열 배열 하나가 주어진다.
문자열 배열에 있는 단어가 2차원 문자 배열에 존재한다면 그 값을 List 에 추가하여 리턴하는 문제
(2차원 문자 배열의 문자는 재사용할 수 없고 상,하,좌,우로만 이동이 가능하다.)

---

풀이 과정

효과적인 탐색을 위해 Trie + DFS 로 접근하였다.
String[] words 를 자료구조에 담고 char[][] board 의 char 변수를 기준으로 탐색을 한다.
끝까지 탐색을 하는 경우 해당 word 가 존재한다는 뜻이기에 정답에 담아준다.

1. String[] words 를 Trie 자료 구조에 담는다.
2. char[][] board 의 모든 값들을 시작 값으로 DFS 탐색을 한다.
3. 중복제거를 위해 Set 자료 구조에 담고 List 로 바꾸어 리턴한다.

1. Trie 자료 구조에 담기

Trie 는 문자열 검색에 효과적인 자료 구조다.
이번 알고리즘 문제에서는 Map 을 이용하여 구현하였다.
Key 는 Character , Value 는 Trie 로 구현한다.
필드에 마지막 문자인지 체크하는 boolean isEndOfWord 변수도 선언해준다.

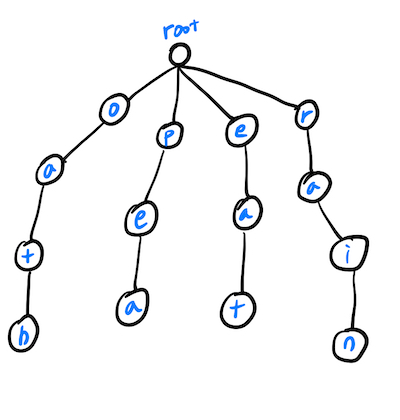
root node 부터 시작한다. 예제 1을 담아보자.

ex) String[] words = ["oath","pea","eat","rain"];

첫 번째 문자열을 가져온다. "oath"
.charAt() 으로 한 단어씩 뜯어낸 후 Key 로 검색을 한다.
.get(Key) 해서 나온 Trie 가 null 이라면 새로 만들어 추가하고
그게 아니라면 다음 node 로 넘긴다.
반복문을 통해 처리한다면 아래 그림과 같은 Trie 자료 구조가 만들어 진다.

2. 탐색

char[][] board 의 시작 인덱스부터 마지막 인덱스까지 탐색을 해야한다.
board[i][j] 를 가져온다면 특정 문자가 등장한다.
예제를 기준으로 char key = board[0][0] 하면 key 변수에는 'o' 가 담긴다.
이 문자로 .get(key) 하게 되면 Trie 객체가 나오게 된다.

.get(key) 으로 나오는 객체가 null 이라면 탐색을 종료한다.
그게 아니라면 DFS 을 이어가는데, 이 때 booelan isEndOfWord 가 true 라면 해당 문자열이 존재한다는 뜻이므로 Set 에 추가한다.

3. return

Set 은 중복 제거를 위해 사용했을 뿐 정답은 List 로 반환해야 한다.
return new ArrayList<>(Set); 으로 반환한다.

---

나의 생각

처음에 DFS 탐색만을 이용하였다가 제한 시간 초과로 풀지 못했다.
문자열 탐색에 효과적인 Trie 자료 구조를 사용해 DFS 탐색을 하여 해결할 수 있었지만
시간 복잡도와 공간 복잡도의 성능이 좋아보이지 않는다.
Trie 자료 구조에 추가할 때와 탐색을 할 때 중복되는 경우의 수를 줄인다면 좀 더 나은 성능으로 풀 수 있을 것 같다.

---

코드

class Solution {

    Set<String> result = new HashSet<>();
    char[][] board;
    boolean[][] visited;

    int[] DX = new int[]{1, -1, 0, 0};
    int[] DY = new int[]{0, 0, 1, -1};

    int m, n;

    public List<String> findWords(char[][] board, String[] words) {
        Trie root = build(words);
        this.board = board;
        
        this.m = board.length;
        this.n = board[0].length;

        this.visited = new boolean[this.m][this.n];

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                String word = "";
                DFS(i, j, word, root);
            }
        }
        
        return new ArrayList<>(result);
    }

    private void DFS(int x, int y, String word, Trie trie) {
        char key = board[x][y];
        Trie node = trie.children.get(key);

        if (node == null) return;

        word += String.valueOf(key);

        visited[x][y] = true;

        if (node.isEndOfWord) result.add(word);

        for (int i = 0; i < 4; i++) {
            int newX = x + DX[i];
            int newY = y + DY[i];

            if (newX >= 0 && newX < m &&
            newY >= 0 && newY < n &&
            !visited[newX][newY]) {
                DFS(newX, newY, word, node);
            }
        }

        visited[x][y] = false;
    }



    private Trie build(String[] words) { 
        Trie root = new Trie();

        for (String word : words) {
            Trie node = root;
            
            for (int i = 0; i < word.length(); i++) {
                
                char key = word.charAt(i);
                Trie child = node.children.get(key);

                if (child == null) {
                    child = new Trie();
                    node.children.put(key, child);
                }
                node = child;
            }

            node.isEndOfWord = true;
        }

        return root;
    }
}

class Trie {
    Map<Character, Trie> children;
    boolean isEndOfWord;

    public Trie() {
        this.children = new HashMap<>();
        this.isEndOfWord = false;
    }

}