909. Snakes and Ladders
문제 분석
2차원 배열이 주어진다.
-1 은 다른 위치로 이동하지 않는다는 뜻.
그 외에 값들은 다른 위치로 이동한다는 뜻이다.
예제를 기준으로 보자면,
int[][] board = new int[][] {
{-1, -1, -1, -1, -1, -1}, // 36~31
{-1, -1, -1, -1, -1, -1}, // 25~30
{-1, -1, -1, -1, -1, -1}, // 24~19
{-1, 35, -1, -1, 13, -1}, // 13~18
{-1, -1, -1, -1, -1, -1}, // 12~7
{-1, 15, -1, -1, -1, -1}, // 1~6
};- 첫 행부터 맨 위의 숫자들을 나타낸다. (
[0][0] == 36)
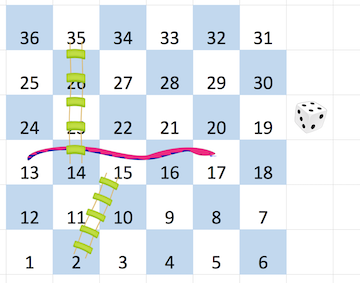
2번은15번으로 이동이 가능하다. (사다리)
14번은35번으로 이동이 가능하다. (사다리)
17번은13번으로 이동이 가능하다. (뱀)
마지막 도착지인 board.length * board.length 곳까지 최소 횟수를 리턴하라.
도착할 수 없다면 -1을 리턴한다.
풀이 과정
사실 문제를 풀 때는 사다리와 뱀의 의미는 없다. 단지 어디로 이동이 가능한지만 판단하면 된다.
- 주어진 배열을 다시 재가공한다. 이동하는 값만 알면 되기 때문에 1차원 배열에 담을 예정.
- 주사위의 경우의 수(+6)와 이동할 수 있는 경우의 수를 구한다.
- 최종 목적지가 등장한다면 이동 횟수를 리턴, 아니면
-1을 리턴.
예제 1 을 기준으로 풀이 과정을 설명한다.
1. 배열 재가공
주어진 배열은 2차원배열이다.
1차원 배열로 바꿔 -1 또는 이동하는 값만 저장하여 사용한다.
(arr[1] = -1 , arr[2] = 15 .... arr[14] = 35 ... 이런식으로 담을 예정)
int[][] board = new int[][] {
{-1, -1, -1, -1, -1, -1}, // 36~31 우측에서 좌측
{-1, -1, -1, -1, -1, -1}, // 25~30 좌측에서 우측
{-1, -1, -1, -1, -1, -1}, // 24~19 우측에서 좌측
{-1, 35, -1, -1, 13, -1}, // 13~18 좌측에서 우측
{-1, -1, -1, -1, -1, -1}, // 12~7 우측에서 좌측
{-1, 15, -1, -1, -1, -1}, // 1~6 좌측에서 우측
};가만보면 좌측에서 우측으로만 읽어야 할 것 같지만
board[row][col] 라고 한다면 col 인덱스가 다르다.
조건문으로 판단하여 값을 담아준다.
private int[] ganerateMap(int[][] board, int size) {
int n = board.length;
int[] map = new int[size + 1];
boolean leftToRight = true;
int index = 1;
for (int i = n - 1; i >= 0; i--) {
if (leftToRight) {
for (int j = 0; j < n; j++) {
map[index++] = board[i][j];
}
} else {
for (int j = n - 1; j >= 0; j--) {
map[index++] = board[i][j];
}
}
leftToRight = !leftToRight;
}
return map;
}2. 주사위의 경우의 수
위의 예시에서 사용한 map 1차원 배열 에는 이동할 수 있는 위치가 담겨져있다.
시작 위치인 1 부터 주사위의 경우의 수를 구하면서 도달할 수 있는 지점을 체크해나갈 것이다.
이때 선입선출의 자료 구조인 Queue 를 사용한다.
먼저 들어온 값이 먼저 나가는 구조를 대략적으로 표현했고, 시작하는 위치를 담아준다.
시작하는 위치는 1이다.
------------------------------------
< < < < < < < < < < 1 < < < < <
------------------------------------Queue 에서 1 을 꺼낸 다음 1 에서 갈 수 있는 위치를 다시 담아준다.
이때 사다리 or 뱀으로 이동할 수 있는 위치도 같이 담아준다.
예제 1 에서는 2가 15로 이동할 수 있기 때문에 15도 같이 넣어준다.
1번으로 이동할 수 있는 곳 - 주사위의 경우의 수 + 사다리 or 뱀
------------------------------------
< < < 2, 3, 4, 5, 6, 7, 15 < < <
------------------------------------다시 Queue 에서 값을 꺼낸 다음 사다리 or 뱀으로 이동할 수 있는 위치도 같이 담아준다.
2 에서 주사위의 경우의 수 (+6) , 사다리 or 뱀으로 이동할 수 있는 위치
3 에서 주사위의 경우의 수 (+6) , 사다리 or 뱀으로 이동할 수 있는 위치
...
15 에서 주사위의 경우의 수 (+6) , 사다리 or 뱀으로 이동할 수 있는 위치
위에서 나올 수 있는 경우의 수를 Queue 에 담아주면 된다.
(이때 재탐색을 방지해야 한다.)
2번으로 이동할 수 있는 곳 - 주사위의 경우의 수 + 사다리 or 뱀
------------------------------------------------------------------------
< < < 8, 9, 10, 11, 12, 13, 16, 18, 19, 20, 21 < < <
------------------------------------------------------------------------위의 로직과 같다.
3번으로 이동할 수 있는 곳 - 주사위의 경우의 수 + 사다리 or 뱀
------------------------------------------------------------------------
< < < 22, 23, 24, 25, 26, 27, 35 < < <
------------------------------------------------------------------------위의 로직과 같다.
4번으로 이동할 수 있는 곳 - 주사위의 경우의 수 + 사다리 or 뱀
------------------------------------------------------------------------
< < < 28, 29, 30, 31, 32, 33, `36` < < <
------------------------------------------------------------------------우리가 찾던 위치가 등장하는 시점에 몇 번 이동 했는지를 리턴해주면 된다.
나의 생각
2차원 배열을 정리해야겠다는 접근법이 성능을 많이 줄여준 것 같다.
처음엔 따로 class 를 만들어서 접근했었다.
board에서 값을 꺼내기 위한 인덱스 int[][]
이동할 수 있는 위치값 int moveTo
횟수 int diceCount 를 필드로 가지고 있었는데
생각해보니 많은 변수들을 가지고 있을 필요가 없다는 걸 깨달았고
단순하게 1차원 배열에 이동할 수 있는 값만 가지고 있게 로직을 변경했다.
코드
class Solution {
public int snakesAndLadders(int[][] board) {
int n = board.length;
int target = n * n;
int[] map = ganerateMap(board, target);
boolean[] visited = new boolean[target + 1];
Queue<Integer> queue = new LinkedList<>();
queue.offer(1);
int count = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int number = queue.poll();
if (number == target) return count;
for (int j = 1; j <= 6; j++) {
int diceNumber = number + j;
if (diceNumber > target) continue;
int nextStep = map[diceNumber] == -1 ? diceNumber : map[diceNumber];
if (visited[nextStep]) continue;
visited[nextStep] = true;
queue.offer(nextStep);
}
}
count++;
}
return -1;
}
private int[] ganerateMap(int[][] board, int size) {
int n = board.length;
int[] map = new int[size + 1];
boolean leftToRight = true;
int index = 1;
for (int i = n - 1; i >= 0; i--) {
if (leftToRight) {
for (int j = 0; j < n; j++) {
map[index++] = board[i][j];
}
} else {
for (int j = n - 1; j >= 0; j--) {
map[index++] = board[i][j];
}
}
leftToRight = !leftToRight;
}
return map;
}
}