1. What is Big-O?

• 데이터의 개수(n)가 주어졌을 때 최악의 경우 컴퓨팅 사칙 연산의 횟수를 의미함.
• 불필요한 연산을 제거하여 알고리즘의 시간복잡도를 쉽게 알아볼 수 있도록 하기 위해 사용

2. Theorems

• 1 computation -> 1
  ex) 1+1 -> O(1)

    for(i=0; i<n; i++){
		//.........
     }

-> O(N)

• 모든 계수를 무시
  • $O(2N) → O(N)$
  • $O(3N^2) → O(N^2)$
  • $O(10) → O(1)$
• 아주 작은 terms 무시
  • $O(N+1) → O(N)$
  • $O(N^2+3N+5) → O(N^2)$
  • $O(2^N+4N^3+5N^2+7N+6) → O(2^N)$

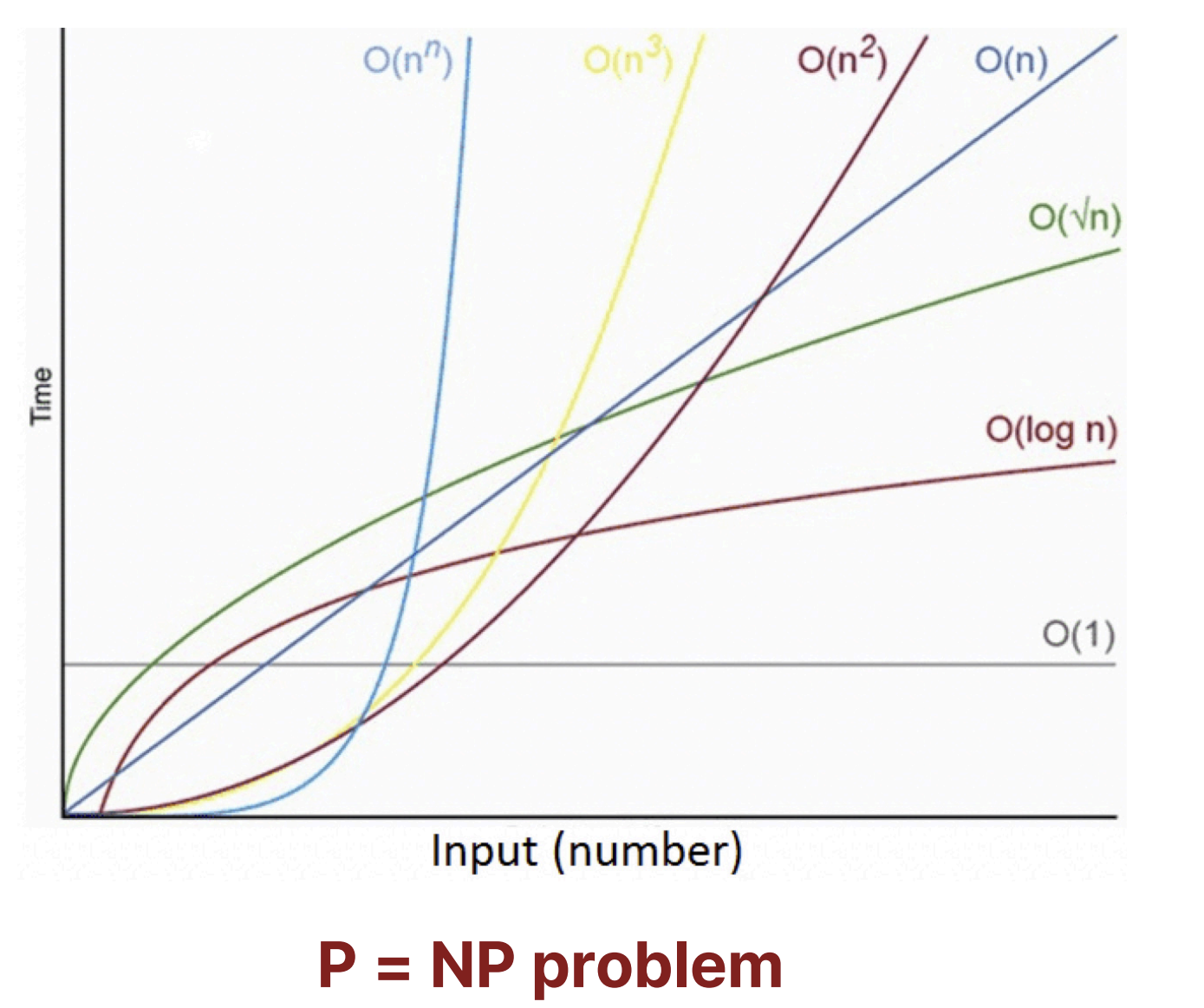
3. Big-O examples and comparison

• $O(1)$ : bounded(by a constant) time
• $O(log{N}) = O(log{2}{N})$: logarithmic time
• $O(N)$ : linear time
• $O(NlogN) = O(N*log_2{N})$: $O(N*log_2{N})$ time
• $O(N^2)$: quadratic time
• $O(2^N)$: exponential time

4. Exercises

• Copy the Array A into empty Array B(A’s length = N) → $O(N)$
  
• Find the max/min item in Array C(C’s length = N) → $O(N)$
  
• Sort the array D(D’s length = N)

  • ex) [7,2,5,6,3] → [2,3,5,6,7]

    → $O(N^2)$

• Find the N-th item in the Fiboonacci series

  • Fibo(N) = Fibo(N-1) + Fibo(N-2)

    → $O(2^N)$