골4
전형적인 플로이드 와샬 문제 유형 중 하나이다.
이차원 리스트를 만들어 노드에서 관계가 발생하지 않는 답을 찾아내는 문제이다.
플로이드 와샬은 코드 자체는 그렇게 어렵지 않다.
하지만 만약 이 유형을 처음 본다면 플로이드 와샬을 딱 떠올리기 힘들 수 있고, 만약 떠올린다 하더라도, 이걸로 뭐? 하는 생각이 들 수 있다.
내가 그랬다.
풀이
핵심은 특정 노드에 대해서 모든 타 노드에서 접근할 수 있거나, 내가 다른 노드로 연결을 할 수 있는가 이다.
두 가지 조건 중 하나만 충족하면 이것은 연결되었다고 한다.
그러므로 플로이드 와샬을 이용해서 최소경로를 찾는것이 아니라, 모든 노드의 경로를 1로 만들어준다고 생각하면된다.
만약 응용을 한다면, 가장 최소의 값으로 특정 노드로 연결되는 노드를 찾아라 하는 문제도 가능할 것 같다.
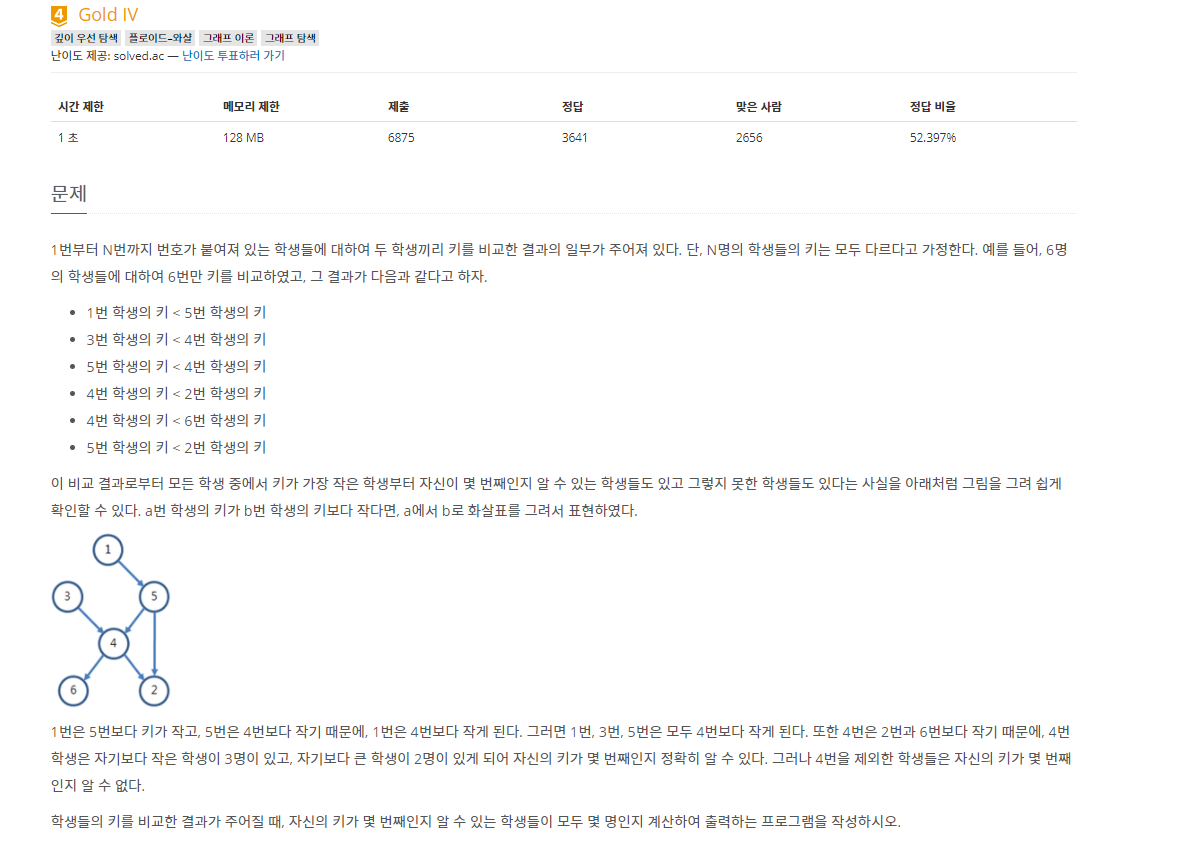
예를 들어서 4번 노드의 경우, 1번, 3번, 5번 노드 -> 4번 이라는 관계가 형성된다.
또한 4번 -> 6번, 2번 이라는 관계도 형성된다.
때문에 4번 노드는 문제에서 요구하는 키가 몇번째인지 알 수 있는 학생이다.
여기까지 파악했다면 그럼 저 관계를 어떤 방식을 통해 파악할 수 있는지를 알아야 한다.
graph라는 이차원 배열을 만들었으면
for문을 돌리면서 graph[i][4] graph[4][i](4번 노드를 예를들어) 이 둘 중 하나의 값이 1이라면 4번노드가 해당 노드로 연결될 수 있다는 의미이다.
반대로 둘 값이 모두 INF 라면 연결될 수 없다는 의미.
반드시 2차원 배열을 그려서 직접 짝지어 보면서 파악해 봐야한다. 안 보이던 것들이 보인다.
N, M = map(int, input().split(" "))
INF = int(1e9)
graph = [[INF] * (N+1) for _ in range(N+1)]
def solution():
for i in range(1, N+1):
graph[i][i] = 1
for _ in range(M):
a, b = map(int, input().split(" "))
graph[a][b] = 1
for k in range(1, N+1):
for i in range(1, N+1):
for j in range(1, N+1):
if graph[j][k] + graph[k][i] < INF:
graph[j][i] = 1
check = True
ans = 0
for i in range(1, N+1):
for j in range(1, N+1):
if graph[i][j] == INF and graph[j][i] == INF:
check = False
break
if check:
ans += 1
check = True
print(ans)
solution()
