그래프

그래프 정의

객체 간에 짝을 이루는 구조를 나타내기 위한 가장 유연한 자료구조

• vertex : (node, point) 각 객체를 나타내는 단어.
• edge : 각 vertex를 잇는 간선을 의미. 이 edge 는 vertex single로도 연결되고 두 vertex에 여러 edge가 존재할 수도 있다.
• Edge는 무향(Undirected) 또는 유향(Directed)일 수 있다.
• Edge에는 가중치(Weight)가 있을 수 있으며, 이는 연결의 강도를 나타낸다.

트리와의 차이

• 트리는 방향성 비순환 그래프라고 할 수 있음(DAG) : Directed Acyclic Graph
• 트리에는 회로(Circuit) 이 없으며, 루트에서 리프노드로의 방향성이 존재
• 트리의 경우 특정 노드에서 특정 노드로 접근하는 path 가 무조건 1개가 존재하지만, 그래프의 경우에는 여러개가 존재할 수 있음. (edge들의 순서)

그래프 종류

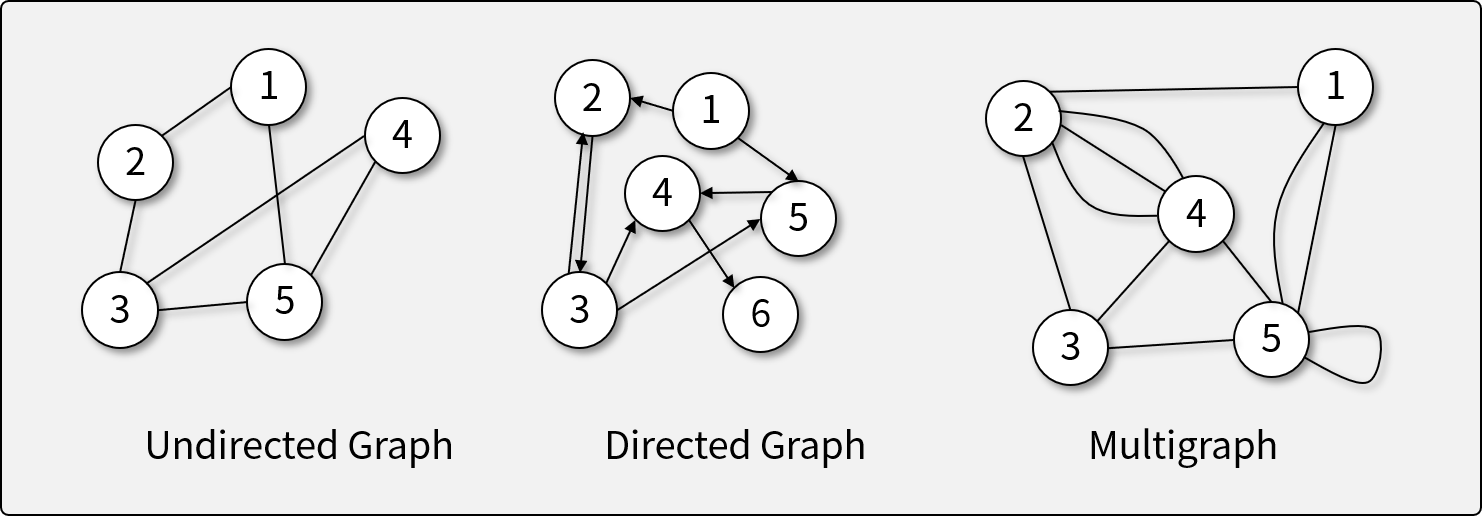
무향 그래프 (Undirected Graph) - 화살표가 X = 양쪽 모두 이동 가능
유향 그래프 (Directed Graph)
다중 그래프 (Multigraph)

그래프 관련 용어

path : 특정 노드에서 특정 노드까지 접근하는 경로

• 트리의 경우 특정 노드에서 특정 노드로 접근하는 path 가 무조건 1개가 존재하지만, 그래프의 경우에는 여러개가 존재할 수 있음. (edge들의 순서)

circuit : path 중 자기 자신으로 돌아오는 path 를 circuit 이라 함.
부분 그래프 (Subgraph) - 어떤 그래프에 속하는 그래프
연결 그래프 (Connected Graph) - 임의의 두 Vertex 사이에 경로가 존재하는 그래프

그래프는 순서가 존재하지 않음. 트리와 다르게. 트리는 순서가 존재해서 left, right 순으로 작동하는게 일반적임

그래프의 구현 방법

인접리스트(adjacency list)

특정 노드의 번호를 인덱스로 삼아 해당 노드와 연결된 노드를 원소로 넣어 표현하는 방법

데이터와 edge가 적고 밀도가 낮을수록 유리한 방법

인접행렬

데이터의 dense가 높으면 유리함.

-> 기본적으로 공간복잡도 O(n^2) 이라, 조금만 데이터가 커져도 사용할 수 없음. but 시간을 절약해줌

ex) SNS 의 경우 엄청난 그래프가 존재하는데, 특정 범위의 그래프만 부분집합으로 뽑아내서 인접행렬을 만들어 사용함. 모든 집합에 대해 인접행렬을 구성하는 건 불가능

그래프의 탐색 방법

bfs(breadth first search)

• 두 Vertex 사이의 최단 경로 or 임의의 경로를 찾을 때 사용
• 트리와 달리 특정 Node의 방문 여부 visited를 검사해야 함
• Queue를 이용하여 반복적(Iterative)인 방법으로 손쉽게 구현 가능

dfs(depth first search)

• 모든 Vertex를 방문하고자 할 때 주로 사용 (순회)
• 트리와 달리 특정 Node의 방문 여부 visited를 검사해야 함
• 재귀(Recursive) 함수를 이용하여 전위 순회의 형태로 구현