[WIL] 자료구조 & 알고리즘

이번주에 배운것

이번주는 자료구조의 기초와 여러 알고리즘 문제를 풀어봤으며,
아래에는 이번주에 배운 6개의 자료구조를 간략히 정리해보았다.

배열

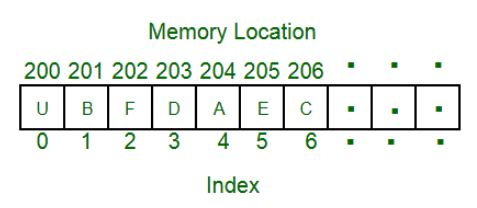
가장 기본적인 데이터 구조로, 생성시 설정된 셀의 수가 고정되고 각 셀에는 인덱스 번호가 부여된다.

• 인덱스는 0부터 시작하고, 컴퓨터는 인덱스 0의 메모리 주소를 가지고 있고 이것으로 각 셀의 데이터에 접근할 수 있는 것이다.

• 인덱스 -1로 음수를 이용하면 배열의 뒷 요소부터 거꾸로 접근할 수 있다.

• 더 복잡한 자료 구조를 구현할때 이용되고, 엑셀의 스프레드시트처럼 직사각형의 테이블, 수학적 벡터및 행렬을 구현하는데 사용된다.

  

스택

먼저 들어온 요소부터 쌓이며 순서가 보존되는 선형 데이터 구조이고, 마지막에 들어온 요소부터 처리하는 LIFO 매커니즘을 가지고 있다.

• push(), pop() 을 이용하여 입력과 출력이 한 방향에서만 이뤄진다.

  • Python - push() => append()

• 가장 마지막에 들어온 요소부터 다시 순차적으로 처리하고 싶을때 사용한다.
  => 브라우저의 뒤로가기, 실행취소, 재귀호출 등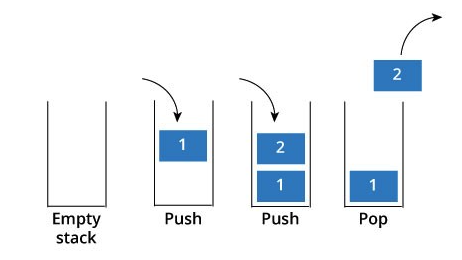

  

큐

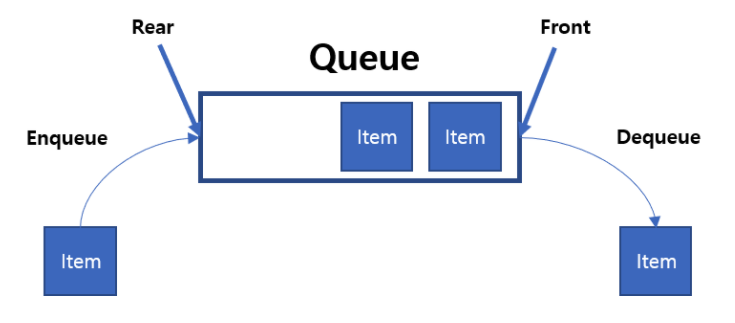
가장 먼저 입력된 요소를 가장 먼저 처리하는 FIFO 매커니즘을 가지고 있다.

• Rear에서는 append()를 이용하여 삽입만 이뤄지고, Front에서는 popleft()를 이용하여 삭제만 이뤄진다.

  • Collections 모듈의 deque()를 이용해야 된다.
  • pop(0)을 이용한다면 O(N) 시간 복잡도를 가지지만, popleft()는 O(1)의 시간복잡도다.

• 순서에 민감한 데이터나 특정 대기열 처럼 가장 먼저 입력받은 데이터 순으로 처리할때 이용된다.

  

연결리스트 - Singly

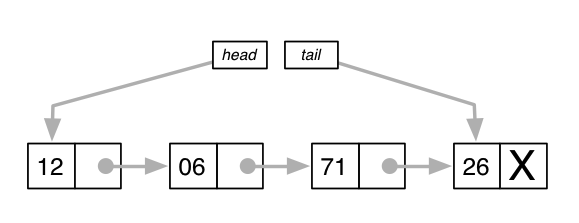
메모리에 있는 요소의 물리적 배치를 이용하지 않고, 노드 포인터를 참조하는 시스템을 이용하는 데이터 구조이다.

• 각 노드에 데이터와, 다음 데이터를 가리키는 포인터가 같이 들어있다.

• 데이터 삽입 및 삭제시 배치의 재구성이 필요하지 않기 때문에 효율적이다.

  • 다음 데이터를 가리키는 포인터만 바꿔주는 것이다.

  

해시테이블

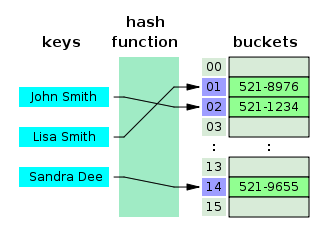
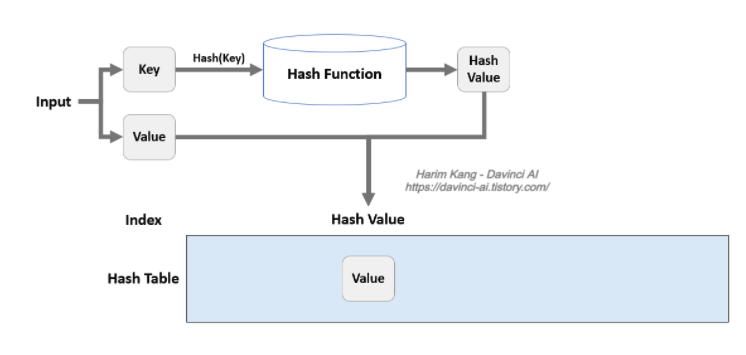
대량의 정보를 저장하고 특정 요소를 효율적으로 검색할 수 있는 데이터 구조로, 테이블 내의 더 작은 서브 그룹인 버킷에 key-value를 한쌍으로 담고있다.

• Key를 해시 함수로 해싱하여 해시라는 고유한 숫자(index)로 변환하여 저장하고, 이 해시 숫자가 실제 값이 저장되는 버킷을 가리킨다.
• 원하는 값의 검색이 빠르고 효율적이지만, 일정 이상으로 공간이 늘어난다면 심각한 성능 저하를 나타낸다.
  • 로드팩터의 비율에 따라서 해시 함수를 재작성 하거나, 해시 테이블의 크기를 조정할지 결정된다.
• 해시값의 충돌이 최소화되고 해시 테이블 전체에 균일하게 분포되는 해시함수가 좋은 해시함수다.
  • 해시 충돌시 해결 방법은 separate chaining과 open addressing이 있다.

그래프

노드(or 정점)와 노드를 연결하는 간선으로 이루어진 자료 구조이다.

• 루트 노드와 부모와 자식이라는 개념이 존재하지 않고, 이어진 간선이 없을수도 있다.
• 그래프는 크게 방향(Directed), 무방향(Undirected) 그래프가 존재한다.
  • 방향 그래프는 두 정점을 연결하는 간선에 방향이 있기 때문에 가리키는 방향으로만 이동할 수 있다.
  • 무방향 그래트는 두 정점을 연결하는 간선에 방향이 없기 때문에 양방향으로 이동할 수 있다.
  • 이외에도 가중치(weighted), 연결(connected), 비연결(disconnected), 순환(cycle), 비순환(acyclic) 등 다양한 그래프가 있다.
• 인접 행렬과 인접 리스트로 구현할 수 있다.
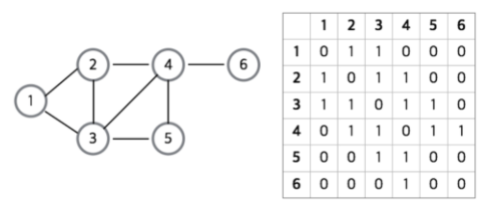
  • 인접 행렬(Adjacency matrix) - Boolean martrix
    1. 그래프의 노드를 2차원 배열로 만들어 인접 정점은 "1" 아니라면 "0"을 넣어준다.
    2. 2차원 배열이 필요하기 때문에 필요 이상의 공간이 낭비된다.
       
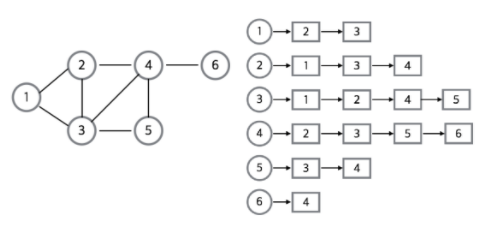
  • 인접 리스트(Adjacency list)
    1. 그래프의 노드를 리스트로 표현한것으로, 해당 노드의 인접노드만 리스트로 담겨 있다.
    2. 필요한 만큼의 공간만 사용하기 때문에 공간의 낭비가 적다.
       
• 그래프의 탐색
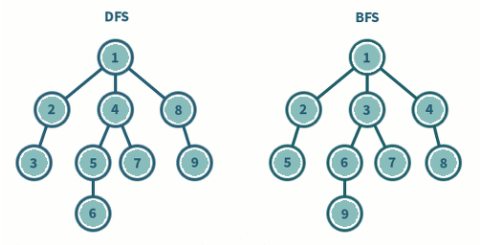
  • DFS(Depth First Search)
    1. 시작 정점에서 왼쪽이나 오른쪽부터 시작하여 갈 수 있는 최대한의 깊이로 들어가고, 더이상 연결된 인접 노드가 없다면 이전 노드로 돌아가는 방식으로 그래프를 순회하는 방식이다.
    2. 재귀호출이나 스택을 사용하여 이용할 수 있다.
  • BFS(Breadth First Search)
    1. 시작 정점에서 시작 정점에 인접한 모든 노드를 우선 방문을 하고 다 방문하였다면 인접 노드의 인접노드를 다 방문하는 방식으로 그래프를 순회하는 방식이다.
    2. Queue를 이용하여 현재 위치에서 갈 수 있는 모든 인접 노드를 넣는 방식으로 이용할 수 있다.

📌 회고

일주일간 다양한 자료구조와 여러 알고리즘 문제를 처음 접해보았기 때문에 현재 내가 공부하고 있는 방법이 맞는건지 의심도 든다.

현재는 문제를 많이 접해보지 못했기 때문에 솔직히 문제를 보고 어떤 방식으로 풀어야겠다 라는게 떠오르지 않아서 최대 1시간까지 고민한 뒤 다양한 풀이법을 보고 내가 이해하기에 적절한 코드를 찾아서 정리하고 코드를 봐도 이해하지 못하는 경우에는 디버깅으로 한 단계씩 다 풀어서 그려보거나 유튜브의 풀이 영상을 참고하고 있다.

문제는 비슷한 문제를 마주하더라도 자료구조를 전혀 매칭하지 못하거나 머릿속에 코드가 떠오르지 않기 때문에 현재 잘하고 있는건지 모르겠다.

우선, 자료구조에 대하여 조금더 깊이 공부하며 일주일 더 같은 방법으로 공부를 진행해보고 진전이 없다면 다른 방법을 찾아봐야 될 것 같다.