TIL #23

기사단원의 무기

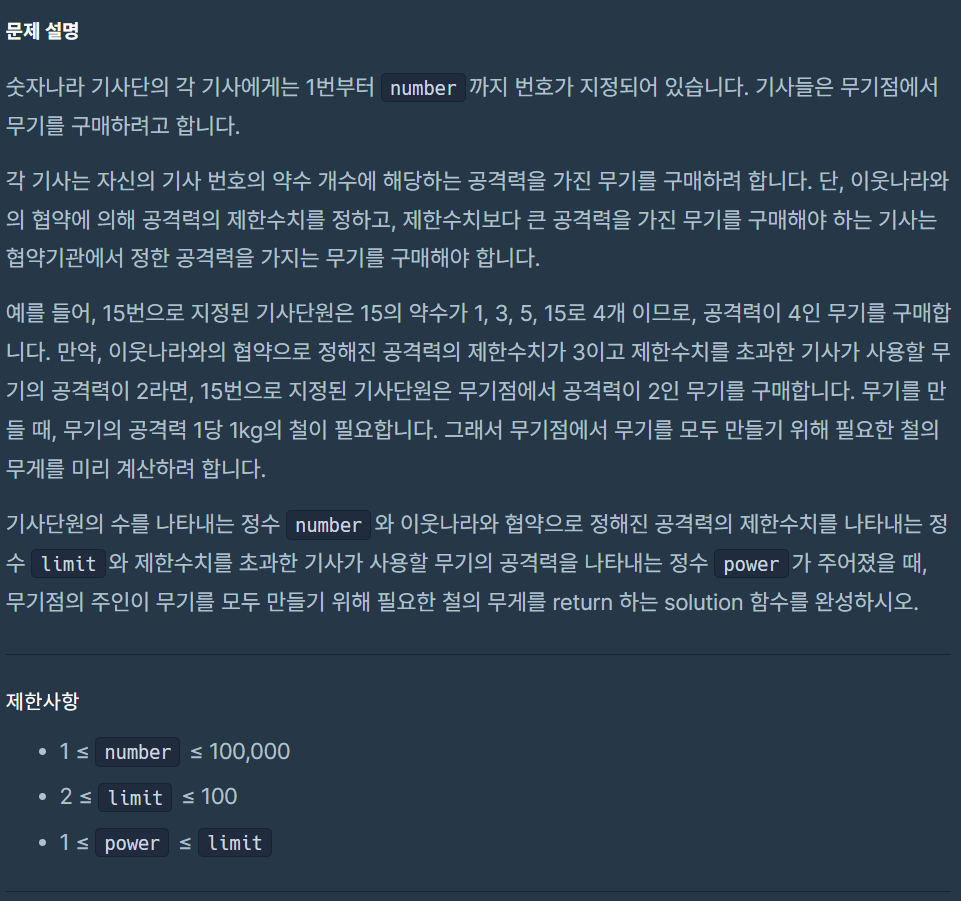
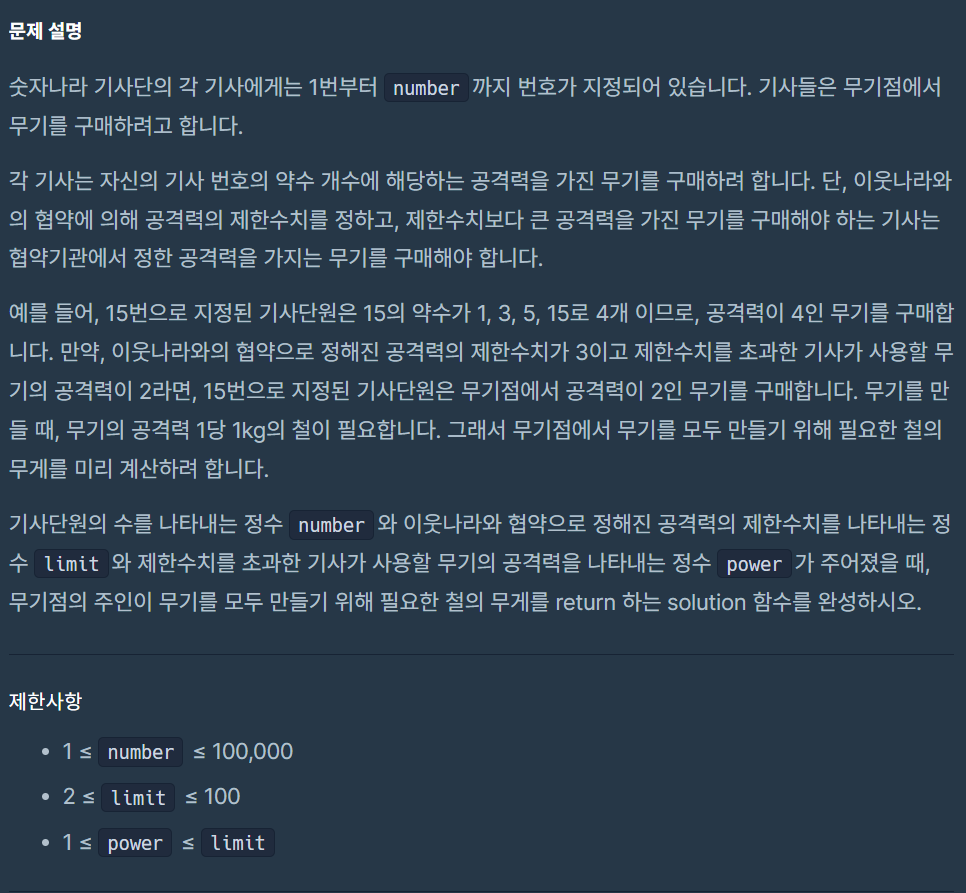
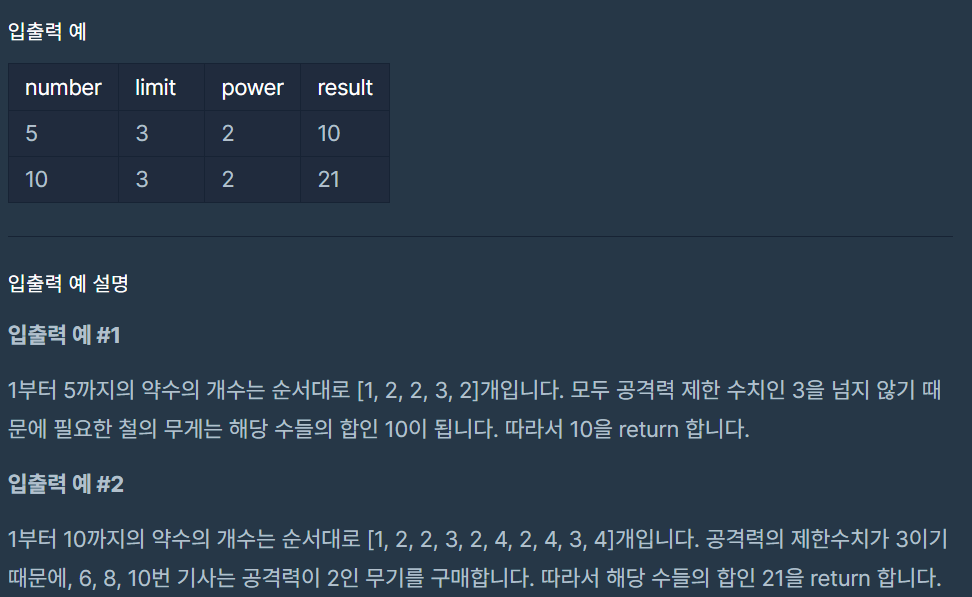
1부터 number 까지의 숫자들의 약수의 개수들을 구하고 제한된 개수(limit)가 넘어가면 power로 대체 해준다.

처음에는 간단하게 모든 수를 1부터 반복해 약수를 구했는데 제출했을때 실행시간이 초과되어 시간을 더 단축 할 수 있는 방법을 사용해야 했다.

---

나의 풀이

class Solution {
    fun solution(number: Int, limit: Int, power: Int): Int {
        var answer: Int = 0
        for( i in 1..number){
            //약수의 개수 구해서 answer에 더하기
            var count = 0
            for( j in 1..i){
                if(i % j == 0){
                    count++
                }
            }
            //제한수치가 넘어가면 power를 더하기
            if(count > limit){
                answer += power
            }else{
                answer += count
            }
        }
        return answer
    }
}

위 코드에서 시간이 초과되어 아래코드로 변경

class Solution {
    fun solution(number: Int, limit: Int, power: Int): Int {
        var answer: Int = 0
        for( i in 1..number){
            var count = 0
            for ( j in 1..Math.sqrt(i.toDouble()).toInt() ) {
                if(i % j == 0){
                    count++
                    if(j != i / j){
                        count++
                    }
                }
            }
            
            if (count > limit) {
                answer += power
            } else {
                answer += count
            }
        }
        return answer
    }
}

제곱근으로 약수를 구해준다.
약수일 경우 카운트해주고 해당 수가 제곱근이 아니라면 한번 더 카운트해준다.

---

다른사람의 풀이

class Solution {
    fun solution(number: Int, limit: Int, power: Int): Int {
        return IntArray(number) { getCount(it + 1) }.fold(0) { acc, v ->
            if (v > limit) acc + power
            else acc + v
        }
    }

    private fun getCount(n: Int): Int {
        var count = 0
        var i = 1
        while (i * i < n) {
            if (n % i++ == 0) count += 2
        }
        if (i * i == n) count++
        return count
    }
}

---

에라토스테네스의 체를 변형하여 사용하기
에라토스테네스의 체를 사용하면 소수를 찾을 수 있는데 이를 변형해 약수의 개수를 찾는데 사용할 수 있다고 한다. 이를 이용하면 약수의 개수를 찾는 알고리즘을 더 빠르게 할 수 있고 큰 수의 계산을 할때 효과적이다.

class Solution {
    fun solution(number: Int, limit: Int, power: Int): Int {
        var answer = 0
        val divisorCounts = IntArray(number + 1) { 0 }
        for (i in 1..number) {
            for (j in i..number step i) {
                divisorCounts[j]++
            }
        }
        for (i in 1..number) {
            val count = divisorCounts[i]
            answer += if (count > limit) power else count
        }
        return answer
    }
}

number크기의 배열을 추가해주고 배열에서 i의 배수(index)에 해당하는 요소들을 증가시킨다.