TIL #3

최대공약수와 최소공배수

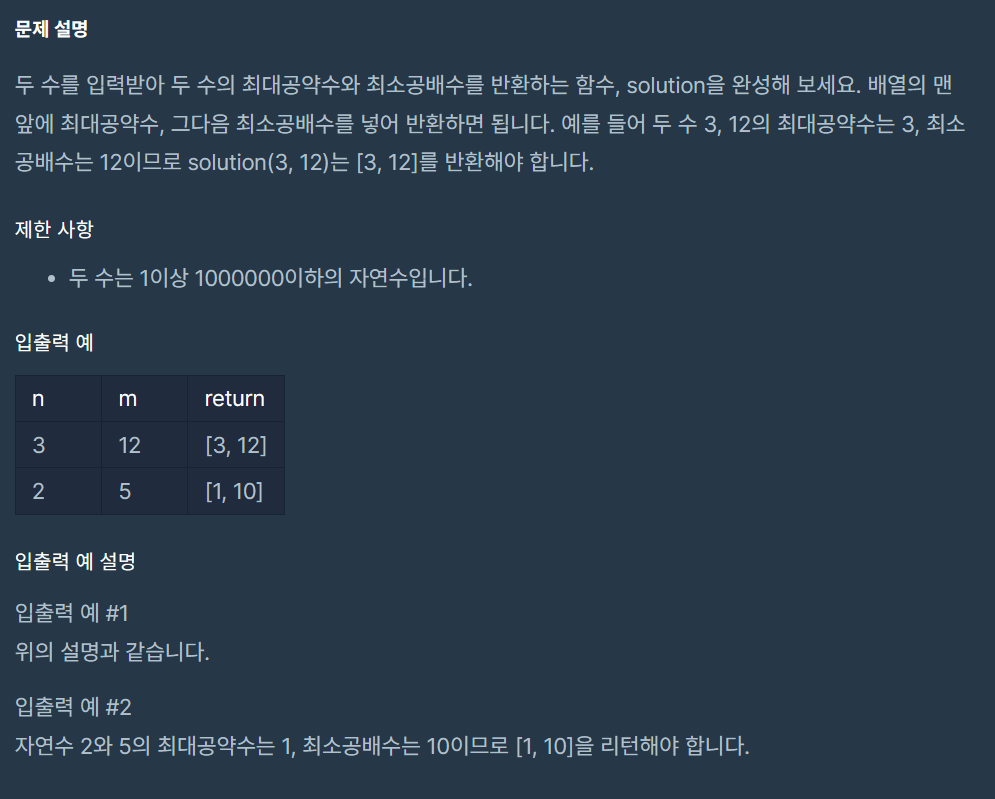
최대공약수(GCD)와 최소공배수(LCM)를 구하는 문제

최대공약수는 유클리드 호제법으로 구할 수 있는데 최초의 알고리즘이라고 한다.

a와 b를 나눈 나머지가 0이면 a,b의 최대공약수가 b가 된다.
0이 아니면 나머지가 0이 될 때까지 a에 b를 넣고 b에 나머지를 넣고 최대공약수를 구한다.

최소공배수는 처음 a와 b를 곱하고 최대공약수를 나누면 된다.

---

처음 풀이

class Solution {
    fun solution(n: Int, m: Int): IntArray {
        var gcd = 0
        var a = n
        var b = m
        while(true){
            if (b % a == 0){
                gcd = a
                return intArrayOf(gcd, n * m / gcd)
            } else {
                var c = b % a
                b = a
                a = c
            }
        }
    }
}

while을 수정

class Solution {
    fun solution(n: Int, m: Int): IntArray {
        var gcd = 0
        var a = n
        var b = m
        while(b ! = 0){
           var c = a
            a = b 
            b = c % b
        }
        
        return intArrayOf(a, n * m / a)
    }
}

---

다른 사람 풀이

class Solution {
    fun solution(n: Int, m: Int): IntArray {
        val gcd = gcd(n, m)

        return intArrayOf(gcd, n * m / gcd)
    }

    tailrec fun gcd(a: Int, b: Int): Int = if (b == 0) a else gcd(b, a % b)
}

tailrec 꼬리재귀함수
함수의 마지막에 자기자신을 호출하는 형태의 함수