TIL #45

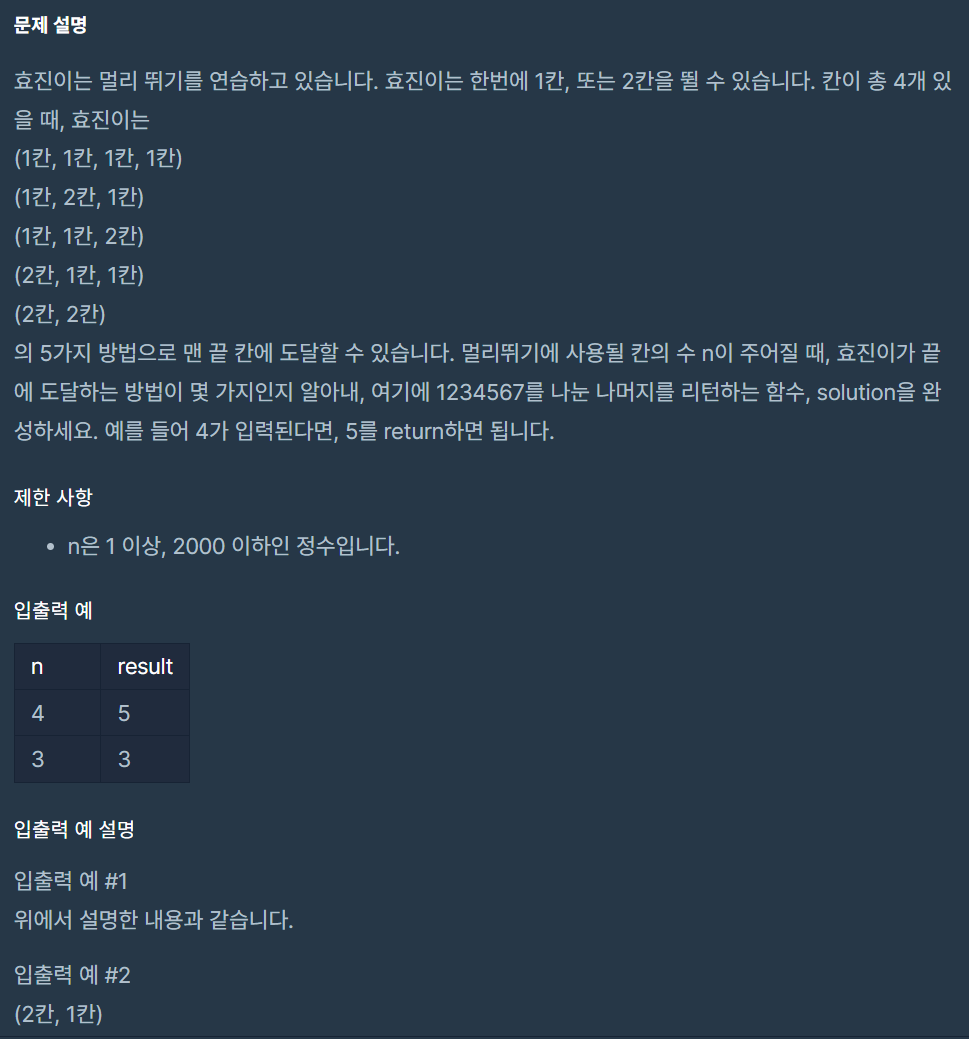
멀리뛰기

1과 2만 가지고 n을 만들 수 있는 경우가 몇개인지 구해야 한다.

어떻게 풀지 고민하다가 n이 1일때부터 6일때까지의 숫자를 손으로 구해보니 뭔가 규칙성이 있는 듯한 숫자들이 나왔다. 그래서 좀 더 생각을 해봤는데 얼마전에 피보나치 수열 문제를 푼게 생각나서 피보나치 수열이란걸 알게되 해당 풀이방식으로 풀게 되었다.

피보나치수열이 DP의 대표적문제라고 해서 DP에 대해 공부를 해봐야 할 것같다.

---

나의풀이

class Solution {

    fun solution(n: Int): Long {
        var answer: Long = 0
        var a = 1L
        var b = 0L
        for(i in 1..n){
            answer = a + b
            var temp = a
            a = a % 1234567+ b % 1234567
            b = temp
        }
        return answer % 1234567

    }

}

처음에 피보나치수열을 구했는데 테스트케이스에서 틀린 문제가 나왔다. 이유는 수가 너무 커져서 그런것이었다. 그래서 1234567로 나눈 나머지로 계속 계산해 큰수가 나오지 않게 풀어주었다.

---

다른사람의 풀이

class Solution {
    fun solution(n: Int): Long {
        var answer: Long = 0
        if(n == 1) return 1
        if(n == 2) return 2
        
        val dp = LongArray(n + 1)
        dp[1] = 1
        dp[2] = 2
        
        for(i in 3..n){
            dp[i] = (dp[i-2] + dp[i-1]) % 1234567
        }
        return dp[n]
    }
}