[알고리즘] 합병 정렬(Merge Sort)

---

합병 정렬 기본

• 문제를 분리하고 각각을 해결한 후 다시 합쳐서 해결하는 분할 정복(Divide & Conquer) 방식을 적용한 알고리즘
• 안정적인 정렬 방법. 입력 데이터의 분포에 상관 없이 좋은 성능을 유지
• 배열을 사용할 경우 임시 배열을 사용해야하며, 배열의 크기가 커지면 성능이 떨어질 수 있음

---

정렬 과정

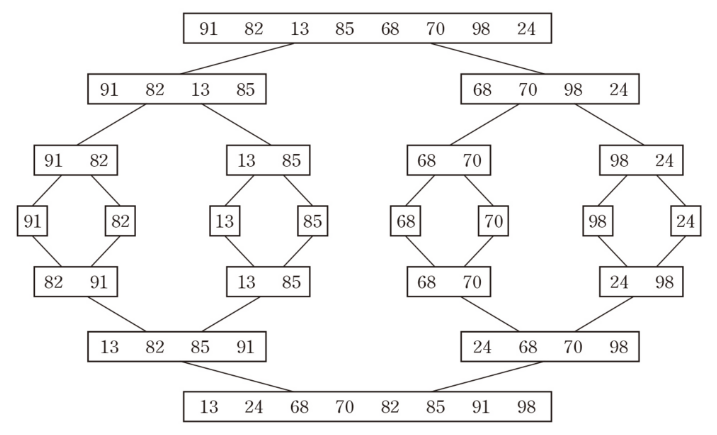
• 초기 배열을 2개의 배열로 분할(Divide)
• 각 부분배열을 병합 정렬을 재귀호출하여 정렬(Conquer)
• 부분배열을 하나의 배열로 병합(Combine)

과정 예시

---

시간 복잡도

• 평균의 경우 : $O(Nlog_2N)$
• 최악의 경우 : $O(Nlog_2N)$
• 최선의 경우 : $Ω(nlogn)$

---

구현

mergeSort()

정렬 로직에 있어, 핵심이 되는 메소드

public void mergeSort(int[] array, int left, int right) {
    
    if(left < right) {
        int mid = (left + right) / 2;
        
        mergeSort(array, left, mid);
        mergeSort(array, mid+1, right);
        merge(array, left, mid, right);
    }
    
}

퀵 정렬과의 차이점
퀵 정렬 : 피벗(pivot) 을 통해 정렬 -> 영역을 쪼갬
합병 정렬 : 영역을 조깰 수 있을 때까지 쪼갬 -> 정렬

merge()

public static void merge(int[] array, int left, int mid, int right) {
    int[] L = Arrays.copyOfRange(array, left, mid + 1);
    int[] R = Arrays.copyOfRange(array, mid + 1, right + 1);
    
    int i = 0, j = 0, k = left;
    int ll = L.length, rl = R.length;
    
    while(i < ll && j < rl) {
        if(L[i] <= R[j]) {
            array[k] = L[i++];
        }
        else {
            array[k] = R[j++];
        }
        k++;
    }
    
    // remain
    while(i < ll) {
        array[k++] = L[i++];
    }
    while(j < rl) {
        array[k++] = R[j++];
    }
}

이미 합병의 대상이 되는 두 영역이 각 영역에 대해서 정렬이 되어있으므로, 단순히 두 배열을 순차적으로 비교하면서 정렬할 수 있음

합병 정렬은 순차적인 비교로 정렬을 진행하므로, LinkedList 의 정렬이 필요할 때 사용하면 효율적

• LinkedList 를 퀵 정렬을 사용해 정렬할 경우, 퀵 정렬은 임의 접근
• LinkedList 는 삽입, 삭제에 유용하지만 접근 연산이 비효율적이므로, 임의로 접근하는 퀵정렬을 사용하면 비효율적임