[자료구조] Stack을 이용한 Iterative DFS 구현

KG·2021년 4월 21일
DFSstack자료구조
16

자료구조 with JS

목록 보기
2/4
post-thumbnail

Intro

자바스크립트는 알고리즘 풀이에 좋은 언어는 아니다. (맨날 알고리즘 포스팅에 이 말을 하는 것 같다..) 다른 언어에 비해 지원되지 않는 부분이 있고, 이를 고려하지 않는 대부분의 알고리즘 시험 환경에서는 직접 자료구조를 구현해서 풀어야 통과하는 경우도 심심찮다. 그러니까 여러분은 JS를 집어 던지고 파이썬이나 C++로 알고리즘을 푸는 것을 적극 추천한다.

본론으로 돌아와서 해당 포스트에서는 DFS 를 Iterative 하게 구현하는 법을 살펴볼 것이다. Iterative의 사전적 의미는 '반복적인' 이라는 뜻인데, 이는 흔히 각 언어에서 반복문을 통해 순차적으로 접근이 가능한 자료형을 말한다. JS 에서는 Array, Map 등과 같은 자료형이 기본적으로 Iterative 하다. 자바에서와 비슷하게 Iterator를 직접 구현할 수도 있다. 하여간 오늘의 메인 주제는 Iterative 자체가 아니니 이쯤하고 넘어가도록 하자. 쉽게 말해 Iterative 하다는 것은 적어도 자바스크립트에서 for ... in / for ... of 와 같은 반복문으로 돌릴 수 있느냐로 어느정도 판가름할 수 있을 것이다.

Iterative DFS

Iterative DFS는 DFS를 주로 Stack을 이용해서 구현하는 것을 말한다. 보통 DFS를 접할 때 재귀적인 방법으로 구현하는 것으로 많이 배우는 것 같다. (적어도 난 그랬다) DFS 알고리즘을 구현할 때 크게 두 가지 방법으로 접근할 수 있다.

  1. 재귀호출 방식
  2. Stack을 이용하여 구현

보통 1번 방식으로 많이 구현하는 이유는, 재귀호출 방식이 더 이해하기 또는 구현하기 편리한 경우가 많기 때문이다. "재귀호출 흐름이 간단하다고?" 라는 의문이 들 수 있겠지만 재귀로 풀이하는게 익숙하다면 확실히 더 편리하고, 그렇지 않더라도 DFS 에서 만큼은 재귀가 더 강점을 지니는 것 같다.

그렇다면 왜 굳이 편리한 재귀방식을 두고 Stack을 이용해서 구현해야 하는지에 대한 의문이 들 수 있다. 앞서 DFS 관련 알고리즘 문제를 포스팅 하면서 매번 자바스크립트에 대한 불평을 했는데, 관련 글을 읽어보았다면 어느 정도 의문을 해소할 수 있을 듯 하다. 결론부터 말하자면 자바스크립트로는 대부분 DFS 알고리즘에서 주어지는 데이터를 가지고 재귀 호출 방식으로 구현한다면 호출 스택(Call Stack)이 여지없이 터져버린다..! 즉 하고 싶어서 하는 것이 아닌, 울며 겨자 먹기로 어쩔 수 없이 문제 풀이를 위해 Iterative DFS 방식을 채택하는 것이다.. (적어도 난 그렇다..)

자바스크립트 호출 스택

이러한 의문 역시 들 수 있다고 생각한다: "다른 언어에서는 통과가 가능한 알고리즘인데 왜 똑같은 알고리즘인데 자바스크립트에서만 통과가 안 된다는 거지?". 나 역시 매우 억울하다. 그래서 본인은 그나마 자바스크립트랑 닮아 있는 파이썬을 기초수준만 익혀서 실제 코딩테스트에서는 자바 스크립트로 런타임 에러가 주구장창 뜰 때 파이썬으로 옮겨가서 코딩하는 편이다. 놀랍게도 동일한 로직으로 파이썬은 대부분의 문제를 통과한다. 우리가 예시로 살펴볼 프로그래머스의 '모두 0으로 만들기' 문제에서도 이 같은 현상을 볼 수 있을 것이다.

그렇다면 다른 언어는 재귀호출을 잘 버티는데 왜 자바스크립트는 이렇게 연약한 모습을 보이는 것일까? 일단 C++은 실행시간이 너무너무너무 빠르기에 인터프리터 언어 형식인 자바스크립트와 사실 비교 자체가 무례하다. 그러면 동일한 인터프리터 방식 파이썬은 왜? 해당 포스트에서 잠깐 언급한 바가 있는데 파이썬의 경우엔 import sys 를 통해 sys.setrecusionlimit(...)함수를 사용하여 재귀함수 호출 제한을 직접 건드릴 수 있다. 물론 이 값을 무한정 늘릴 수는 없지만 출제측에서 '재귀로 풀지마!'를 의도하지 않은 이상은 대부분 이 값을 조정하여 제한범위 내 풀이가 가능한 경우가 많다.

빙빙 돌아왔지만 핵심을 말하자면 자바스크립트로 DFS를 재귀로 구현하면 다른 언어에 비해 스택 오버플로우가 굉장히 쉽게 터진다. 이는 프로그래머스 환경에서는 죄다 런타임 에러로 뜨게 된다.

브라우저 환경마다 호출 스택의 Maximum Size가 다르고, 또한 호출되는 함수 내부가 어떻게 구현되어 있는지에 따라서도 Maximum Size가 요동치지만 보통 안정적으로 10000번 이상 재귀호출 된다면 우리의 연약한 자바스크립트 호출 스택은 위태위태 하다고 보면 될 것 같다.

실제로 스택 오버플로우 사이트에 올라온 질문을 참고해보면 아래와 같이 간단한 함수를 하나 만들고 이를 무한정 재귀호출 했을때 각 브라우저별로 나타나는 호출 스택의 Maximum Size는 다음과 같았다. 원본은 여기에서 확인할 수 있다.

let i = 0;
function inc() {
  i++;
  inc();
}

try {
  inc();
} catch(e) {
  i++;
  console.log('maximum size : ', i);
}

Internet Explorer

  • IE6: 1130
  • IE7: 2553
  • IE8: 1475
  • IE9: 20678
  • IE10: 20677

Mozilla Firefox

  • 3.6: 3000
  • 4.0: 9015
  • 5.0: 9015
  • 6.0: 9015
  • 7.0: 65533
  • ...

Google Chrome

  • 14: 26177
  • 15: 26168
  • 16: 26166
  • 25: 25090
  • 47: 20878
  • 51: 41753

Safari

  • 4: 52426
  • 5: 65534
  • 9: 63444

Opera

  • 10.10: 9999
  • 10.62: 32631
  • 11: 32631
  • 12: 32631

Edge

  • 87: 13970

본인의 브라우저 환경은 구글 크롬 90버전인데 콘솔창을 켜서 해당 스크립트를 실행하면 13949 밖에 되질 않는다..

하지만 대부분의 코딩 테스트에서는 데이터의 범위를 몇만 수준으로 찔끔찔끔 주는 경우가 없다. 때문에 우리 연약한 자바스크립트는 여기 저기서 펑펑 터져나가게 되는 것이다. 즉 재귀호출로 풀 수 있을 데이터의 양이거나 또는 가지치기가 잘 되어 maximum size 이내로 재귀 호출이 되는 경우엔 DFS 재귀 방식으로도 통과가 가능하겠지만 그 외에 경우엔 재귀호출 방식으로는 통과하기가 매우 힘들다.

Recursive vs. Iterative

계속해서 재귀가 편하다 간단하다라고 하는데, 왜 그렇게 말하는지 몸소 느껴보자. 다음은 프로그래머스 월간 코드 챌린지 시즌2에 제출된 Lv.3 문제이다. 자세한 풀이 방법은 여기를 참고하고 우리는 DFS 구현 파트만 살펴보자.

Recursive DFS

let sum = 0;
const dfs = (start, prev) => {
  for(const next of tree[start]) {
    if(next === prev) continue;
    dfs(next, start);
  }
  
  sum += Math.abs(a[start]);
  a[prev] += a[start];
}

dfs(0, -1);

Iterative DFS

const stack = [ [0,-1] ];
const visit = new Array(a.length).fill(false);
  
let answer = 0;
while(stack.length) {
  const [start, parent] = stack.pop();
    
  if(visit[start]) {
    a[parent] += a[start];
    answer += Math.abs(a[start]);
    continue;
  }
    
  stack.push([start, parent]);
  visit[start] = true;
    
  for(const next of tree[start]) {
    if(!visit[next]) {
      stack.push([next, start]);
    }
  }
}

일단 코드양만 봐도 후자가 더 길다. 물론 단순히 코드양이 많다고해서 불편하다는 것이 아니다. DFS 방식에서 간단하게 구현할 수 있는 부분을 Iterative 에서는 한번 더 생각해주어야 하기 때문이다.

물론 어디까지나 Recursive DFS 가 더 익숙한 관점에서의 이야기! 만약 Iterative DFS 가 더 익숙하다면 오히려 Recursive 방식을 이해하기 똑같이 힘들 것이다.

특히 까다로운 이유 중에 하나는 리프 노드에서 어떤 연산을 시작하여 해당 결과값을 자기의 부모노드로 쭈욱 전달해 최종적으로 루트노드까지 이 값을 가져오는 경우이다. 말로 풀어서 설명하니 뭔 소리인가 할 수 있지만 대부분의 DFS 알고리즘을 요구하는 문제에서 필요로 하는 로직이다. 여기서 예시로 드는 문제 역시 그렇고, 기억은 안 나지만 프로그래머스에서의 다른 DFS 문제 역시 이러한 로직을 요구하는 경우가 더러 있었다.

Recursive DFS 의 경우엔 해당 연산을 모든 탐색이 끝나는 지점에서 수행이 가능하다. 즉, dfs()를 자가호출 하는 반복문이 끝나는 외부의 영역이다. 재귀 호출의 흐름에 익숙하다면 해당 영역이 왜 더 이상 깊이 내려가 탐색할 노드가 없을 때 수행되는 영역인지 알 수 있을 것이다. 말 그대로 해당 영역은 나와 연결된 노드 중에 더 이상 탐색할 공간이 없을때(=> for문이 실행되지 않을 때) 수행되는 공간이기 때문이다. 즉 코드의 흐림이 인간 사고의 흐름과 그나마 비슷하게 흘러간다.

반면 Iterative DFS는 아직 자세히 살펴보지는 않았지만, stack에서 pop을 해놓고, 밑에서 다시 그 값을 넣어주는 해괴한(?) 짓을 하고 있는 것을 볼 수 있다. 그리고 방문 처리를 해주고 다음 노드를 탐색하는 것 같은데, 이들 사이에 갑자기 현재 노드의 방문 여부를 체크해주는 조건문이 들어가있다. 아이러니하게 Iterative DFS 에서는 해당 영역이 위에서 언급한 더 깊이 내려가지 못하는 노드일 때 수행되는 영역이다. 위에서는 반복문이 더 이상 실행되지 못하니까 이러한 영역이 성립되는 것을 다소 쉽게 이해할 수 있는데 Iteratvie 방식에서는 갑자기 중간에 리프노드를 검사하는 흐름이 상당히 낯설다.

이러한 차이점 때문에 보통 재귀 구조로 DFS 를 구현하는 것이 더 편리하다라고 말하는 것 같다. 물론 두 가지 구조를 따로따로 쉽게 이해하는 넘사벽 갓갓들에겐 해당되지 않을 이야기일테지만. 그럼 Iterative DFS 를 하나하나 구현해가며 그 내부 로직을 좀 더 자세히 살펴보도록 하자.

Iterative DFS 방문 구현

Recursive DFS 방문 순서

먼저 재귀 방식으로 구현한 DFS 알고리즘의 흐름을 생각해보자. 1번 노드를 루트노드로 DFS 탐색을 시작한다면 다음 이미지와 같이 흘러갈 것이다. 즉 방문 순서는 (0) -> (1) -> (4) -> (5) -> (2) -> (3) -> (6) 이 될 것이다.

위 과정을 먼저 스택을 이용해 구현해보자. 재귀 함수에서는 다음에 방문할 노드가 있다면 해당 위치에서 다시 자기 자신을 호출하여 넘어가는 식으로 구현 되었다. 따라서 해당 위치에서 계속 깊어지는 방향으로 노드를 탐색할 수 있었다.

Iterative DFS 방문 순서

일단 연결된 노드의 정보들은 연결리스트로 이미 생성되었다고 가정하자. 이를 바탕으로 현재 노드와 연결되어 있는 노드들을 탐색할 수 있을 것이다. 이때 이미 방문한 노드는 재방문을 막아주어야 하기 때문에 별도로 visit 배열을 선언하여 각 노드의 방문 여부를 체크해주자. 그리고 처음에 탐색을 시작할 루트노드 하나를 stack에 포함하여 초기화 해주자.

// 첫 시작 노드를 0번 노드로 지정
const stack = [ 0 ];
// 현재 그래프의 노드 개수만큼 길이를 지정하고 
// 모두 방문하지 않은 상태로 초기화한다.
const visit = new Array(nodes.length).fill(false);

그리고 stack 이 텅텅 빌때까지 우리는 반복문을 돌 것 이다. stack이 비게되는 것은 더 이상 탐색할 노드가 없다는 의미로 탐색을 마쳤다는 의미로 두자. 그러기 위해서는 stack에 들어있는 노드를 하나씩 꺼내야 할 것이다.

여기서 BFS 탐색과 해당 과정이 어느 정도 닮아 있는데, 가장 중요한 차이점은 BFS 탐색의 경우는 큐(Queue) 자료구조를 사용해 FIFO 원칙을 이용하고, DFS를 스택으로 구현할 때는 스택(Stack)을 사용해 LIFO 원칙을 이용한다는 것이다. 왜냐하면 우리는 깊이 위주로 탐색을 해야하기 때문에, 가장 마지막에 담긴 원소를 기준 삼아 계속 depth를 깊게 내려갈 것이기 때문이다.

노드를 하나 뽑았다면, 이 노드는 방문 했다는 것과 같으므로 visit[node] = true 를 통해 현재 노드의 방문 여부를 체크해주자. 그리고 이 노드와 연결되어 있는 노드들이 있다면 해당 노드를 방문했는지 안 했는지를 구분하여, 만약 방문하지 않은 상태라면 stack에 이들을 차례대로 push 하도록 하자. 즉 다음과 같이 구현될 것 이다.

// tree 라는 변수에 그래프 연결리스트 정보가 있다고 가정
while(stack.length) {
  // 가장 마지막에 삽입된 노드를 뽑는다.
  const node = stack.pop();
  
  // 해당 노드를 방문 처리하고
  visit[node] = true;
  
  // 해당 노드와 연결된 노드 중에
  // 아직 방문되지 않은 노드가 있다면 stack에 푸시
  for(const next of tree[node]) {
    if(!visit[next]) {
      stack.push(next);
    }
  }
}

이처럼 DFS를 구현하면 방문 순서는 아래 그림과 같다. 위에 재귀적으로 구현한 DFS와 순서가 달라지는 것을 유의하자! 검정화살표는 현재 노드를 가리키고, 빨간색 테두리는 현재 노드와 연결되있는 노드 리스트를 말한다.

먼저 0번 노드부터 시작하기에 0번과 연결된 1, 2, 3번 노드들이 stack 에 푸시될 것이다. 따라서 아래 그림에서 처럼 stack 에는 [ 1, 2, 3 ] 이 저장될 것 이다.

다음 반복에서 stack.pop() 을 통해 현재 노드를 가져오기 때문에 현재 노드는 3번이 될 것이다. 그리고 3번과 연결된 노드는 6번이 있다. 따라서 stack 에는 [ 1, 2, 6 ] 이 저장될 것 이다.

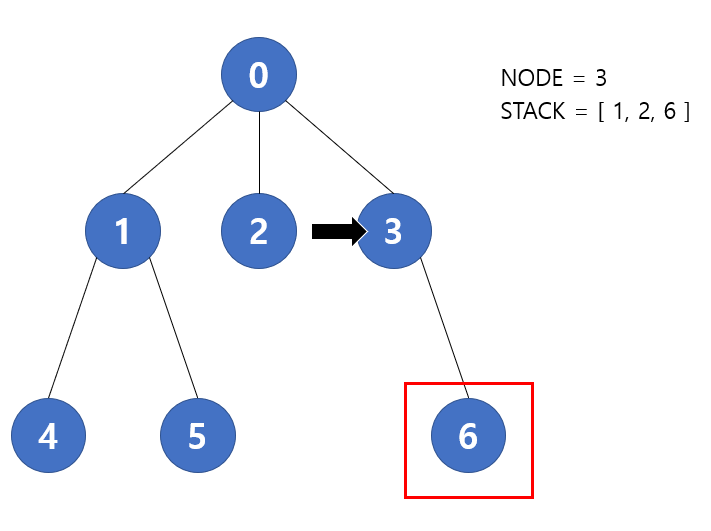
다음 반복에서 stack.pop() 을 통해 6번 노드가 현재 노드가 된다. 그러나 더 이상 방문하지 않은 연결된 노드가 없기 때문에 다음 노드를 탐색하지 않고 반복을 마친다. 따라서 stack 에는 [ 1, 2 ] 이 저장될 것 이다.

다음 반복에서 stack.pop() 을 통해 2번 노드가 현재 노드가 된다. 2번 역시 연결된 노드 중 방문하지 않는 노드가 없기에 반복을 종료한다. 따라서 stack 에는 [ 1 ] 이 저장될 것 이다.

다음 반복에서 stack.pop() 을 통해 1번 노드가 현재 노드가 될 것이다. 1번 노드는 4번과 5번이랑 연결되어 있기에 이들을 stack 에 푸시할 것이다. 따라서 stack 에는 [ 4, 5 ] 가 저장될 것 이다.

다음 반복에서 stack.pop() 을 통해 5번 노드가 현재 노드가 된다. 다음 노드가 없으므로 반복을 종료한다. 따라서 stack 에는 [ 4 ] 가 저장될 것 이다.

다음 반복에서 stack.pop() 을 통해 4번 노드가 현재 노드가 된다. 다음 노드가 없으므로 반복을 종료한다. 따라서 stack 은 [ ] 이 될 것 이고 while 문 조건에 의해 반복을 종료한다. 즉 모든 탐색이 끝나게 된다.

따라서 Iterative DFS 에서의 방문 순서는 (0) -> (3) -> (6) -> (2) -> (1) -> (5) -> (4) 가 될 것이다. 즉 위에서 살펴본 Recursive DFS 방식과 방문 순서가 반대가 된다. 방문 순서를 똑같이 맞추어 줄 수는 있겠지만 사실 DFS 탐색에서 이 방문 순서가 크게 의미가 있지는 않다. 두 경우 모두 정상적으로 DFS 알고리즘에 따라 모든 노드 탐색을 마쳤기 때문이다. 굳이 차이를 두면 Recursive DFS 에서는 작은 값을 우선 방문하는 원칙을 두었고, Iterative DFS에서는 큰 값을 우선 방문하는 원칙으로 탐색이 진행되었다. 이는 우리가 직접 설정해준 값이 아니다. 단지 Recursive 방식과 Iterative 방식 간의 차이점에서 발생하는 근본적인 차이라고 보면 되겠다.

생각보다 간단한데?

라고 생각할 수 있다. 실제로 이해하기도 어렵지 않고 간단하게 구현되었다. 문제는 DFS 탐색 구현 자체가 아니다. DFS 알고리즘 방식을 이용해서 문제를 해결하는 것이 주요 과제이다. 여기서 본격적으로 고민거리가 깊어진다.

다시 Recursive DFS 방식을 살펴보자. 두 가지 방식을 비교하며 제시한 코드를 통해서 이미 두 방식의 리프노드 영역이 서로 다르다는 것은 확인했다. 엄밀히 말하면 리프노드만의 영역은 아니고 더 이상 탐색할 노드가 없는 순간의 노드의 영역이다. 이는 굉장히 중요한데, 이는 리프노드일 수도 있고 자기와 연결된 노드의 탐색을 모두 마치고 돌아온 특정 노드의 부모 노드도 해당되기 때문이다. 즉 그림에서 제시된 빨간 화살표와 분홍 화살표에서 나타나는 것처럼 방문하고 다시 방문한 노드의 부모 노드로 돌아가는 과정이 Recursive 방식에서는 굉장히 자연스럽게 구현이 되어있다. 바로 더 이상 방문할 수 있는 노드가 없는 경우, 즉 for문이 종료되고 다음 시점이 된다.

그러나 위에서 구현한 Iterative 방식을 다시 살펴보자. Recursive 방식에서 처럼 다시 부모 노드로 돌아오는 로직이 있을까? 애석하게도 정답은 No! 이다. Iterative 방식에서는 현재 노드는 항상 pop이 되어 배열에서 사라지기 때문에 현재 노드와 연결된 노드로 내려갔을 때, 부모 노드의 정보에 접근할 수 없다. 게다가 전체 배열에는 방문하지 않는 노드들만 들어가기 때문에 깊이를 우선으로 하여 쭉 내려간 노드에서 탐색이 끝나면, 그 노드의 부모 - 조부모 - 고조부모 - 증조부모 - .... 까지 이어지는 라인을 모두 건너뛰어 가장 상위에 있던 부모노드의 다른 자식으로 건너간다. 위 그림에서 stack 원소의 변화를 보면 이를 알 수 있다.

문제는 대부분 DFS 를 활용해서 문제를 풀이해야 한다면, Recursive DFS 에서 작동하는 로직이 필요하다는 점이다. 대표적으로 이 문제가 그러하다. 앞에서 계속 들먹인 '모두 0으로 만들기'라는 문제이다. 따라서 우리는 위에서 구현한 Iterative DFS를 Recursive DFS와 똑같은 방식으로 만들어주기 위해 추가적인 요소를 구현해주어야 한다.

부모노드를 찾아서..

여러가지 방법이 있겠지만, 가장 직관적인 방법을 택하자. 바로 현재 노드 레벨에서 연결된 부모 노드의 정보를 매핑해주는 것이다. 매핑의 형태는 객체(Object)를 써도 되고 ES7 문법의 Map 자료형을 써도 되고 상관없다. 어차피 부모 노드는 단 한 개 이므로 그냥 배열로 매핑하겠다. 첫 번째 원소는 현재 노드, 두 번째 원소는 해당 노드의 부모 노드로 매핑할 것 이다. 그렇다면 다음과 같이 코드를 수정해야 한다.

// 루트노드는 부모 노드가 없다. 시작노드이기 때문이다.
// 따라서 존재할 수 없는 번호를 지정해주자.
// -1도 가능하고 null, undefined 등 구분할 수 있는 무언가를 넣어주자.
const stack = [ [0, -1] ];
...

while(stack.length) {
  // 구조분해할당을 통해 현재 노드와 부모 노드를 선언
  const [node, parent] = stack.pop();
  
  ...
  
  // next는 현재 노드와 연결된 자식 노드이다.
  // 따라서 next의 부모는 node가 된다.
  stack.push([next, node]);
  
  ...
}

위 과정을 통해 우리는 부모노드를 추적할 수 있다. 그런데 부모 노드에 대한 정보를 넣어주는 것만으로는 다시 되돌아가는 로직을 수행할 수는 없다. 그냥 '해당 노드는 이러한 부모 노드를 가지고 있어'에 대한 정보만 추가되었을 뿐 내부 로직은 처음과 동일하기 때문에 똑같이 부모라인을 모두 건너뛰게 된다. 이를 방지하기 위해 우리는 부득이하게 현재 노드를 pop 하고 나서 다시 stack에 이를 넣어주는 번거로운 일을 해주어야 한다. 무슨 말이나면 다음과 같다.

while(stack.length) {
  // 현재 노드를 꺼내고
  const [node, parent] = stack.pop();
  
  ...
  
  // 현재 노드: 부모 노드를 다시 넣어준다(?)
  stack.push([node, parent]);
  
  ...
}

이 무슨 해괴망측한 짓인가 생각할 수 있다. 물론 둘 사이에 특정 조건이 들어갈 것이다. 일단은 먼저 pop을 해놓고 다시 push를 하는 이상한 상황을 먼저 주목해보자.

우리는 앞서서 pop을 통해 마지막 원소를 기준으로 깊이 우선 탐색을 하는 과정을 봄과 동시에 이 때문에 중간에 있는 부모 라인은 모두 건너뛰고 새로운 라인으로 바로 탐색을 이어가는 것을 살펴보았다. 우리가 DFS를 통해 하려는 연산은 보통 이 건너뛰는 영역에 걸쳐있다. 근본적으로 건너뛰는 가장 간단한 이유는 pop을 통해 부모 단계의 노드를 제거했기 때문이다. 그렇다면 역시 간단하게 생각해서, 다시 현재 노드를 다음 노드가 부모 노드로 인식할 수 있게 넣어주면 되지 않을까? 라는 자연스러운 생각이 들 수 있다. 이 관점에서 우리는 굳이 pop을 해서 꺼내준 [ 현재노드:부모노드 ] 쌍을 다시 푸시해주는 것이다.

그러나 유의할 점이 있다. 아무런 조건 없이 위 로직을 반복하면 반복문이 끝나질 않는다. 즉 무한루프에 빠져버린다. 이는 당연하게도 제거가 이루어 지지 않기 때문이다. 따라서 특정 조건에서는 푸시가 일어나지 않도록 설정해주어야 한다. 여기서 말하는 특정 조건은 무엇일까?

이미 방문하지 않았나..?

제일 처음 구현했던 Iterative DFS 를 생각해보자. 분명히 우리는 가장 마지막 원소를 pop으로 꺼냈고, 그 후에 해당 노드를 방문처리 했다. visit[node] = true로 방문처리 해주지 않았는가! 그런데 위의 로직만 놓고 보면 이미 방문했던 노드를 또 다시 방문하는 것과 다름이 없다. 물론 이전의 부모노드로 돌아가기 위해 그러한 처리를 해주었기 때문에 이는 당연하다. 그러나, 우리는 방문 여부만 체크해주면되지 또 다시 해당 노드에서 연결된 다른 노드들을 탐색해줄 필요는 없다. 왜냐하면 재방문 이전에 첫 방문에서 이러한 작업들을 모두 수행해주었기 때문이다.

중요한 키워드이다. 즉 재방문이 일어났다라는 것은, 해당 노드가 리프노드 였던가, 아니면 리프노드로 부터 하나씩 거슬러 올라가 도착한 부모노드라는 소리가 된다. 즉 재방문하는 경우라면, 리프노드 또는 더 이상 탐색이 불가한 노드의 영역과도 같다. 이는 우리가 처음에 구현한 Itreative DFS 에서는 빠져있던 영역이고, Recursive DFS 에서는 동일하게 존재하는 영역이며, 최종적으로 우리가 Iterative 방식에서도 추가적으로 구현해주고자 한 부분이다! 따라서 pop 이후에 현재 노드의 방문 여부를 체크하여 이미 방문했다면 continue 하도록 설정해준다면 이 영역을 구현할 수 있다!

while(stack.length) {
  const [node, parent] = stack.pop();
  
  // 현재 노드를 하나 뽑았는데
  // 이미 방문한 노드라면 이전에 누군가의 부모노드 였거나
  // 리프노드인 경우이다.
  if(visit[node]) {
    // 따라서 해당 영역은
    // Recursive DFS 영역에서 for문이 종료된 외부 영역과 동일하다
    continue;
  }
  
  stack.push([node, parent]);
  visit[node] = true;
  
  for(const next of tree[node]) {
    if(!visit[next]) {
      stack.push([next, node]);
    }
  }
}

코드와 말로는 이해가 조금 불분명할 수 있다. 똑같이 그림을 통해 일부분만 확인하여 내부 로직을 자세히 살펴보자.

먼저 초기 상태가 다르다. 처음엔 pop을 하고 나서 그대로 진행 했기 때문에 [1, 2, 3] 만 들어 있었지만, 이젠 pop 이후에 방문하지 않은 상태면 다시 해당 노드를 넣어준다. 또한 부모노드 추적을 위해 매핑된 형태로 stack에 들어갈 것이다. 여기서 굵은 파란글씨가 pop 되었다가 다시 push 된 원소를 의미한다.

다음은 3번 노드가 pop이 되고 첫 방문이기 때문에 다시 push 되어 다음 이미지와 같은 상태가 된다.

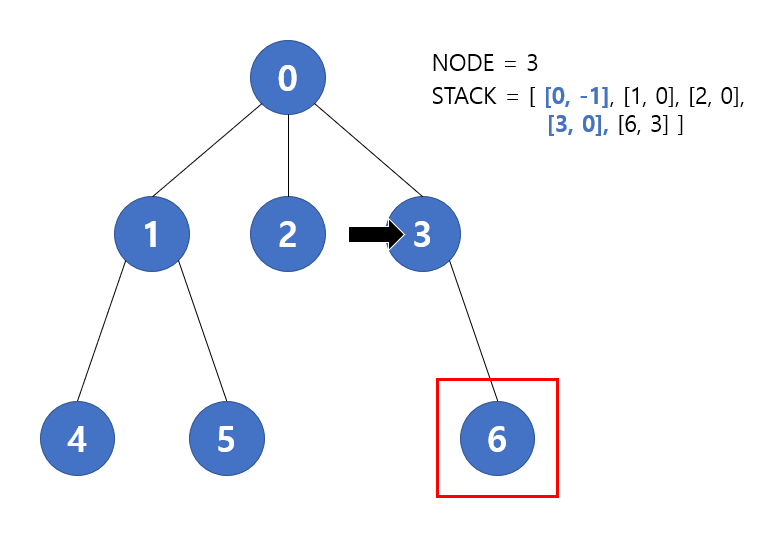
다음은 6번 노드가 pop이 되고 첫 방문이기 때문에 다시 push 되어 다음 이미지와 같은 상태가 된다.

다음 반복에서 pop을 하면 다시 6번 노드가 나오고, 이미 방문했기 때문에 재방문 하는 경우이다. 앞서서 재방문하는 경우는 1. 리프노드와 2. 현재 노드의 부모노드 두 가지로 나뉘게 된다고 했는데 해당 경우는 리프노드의 경우이다. 따라서 탐색을 진행하지 않고 pop만 한 채 다음 반복으로 이동한다.

다음 반복에서 pop을 하면 3번 노드가 나오고, 해당 노드역시 재방문하는 노드이다. 따라서 탐색을 진행하지 않고 바로 다음 반복으로 건너뛰게 된다.

따라서 우리는 부모노드가 누구인지 배열의 두 번째 원소를 통해 알 수 있고, 더 이상 깊게 내려갈 수 없을때 이전에 방문했던 부모노드를 차례대로 거슬러 올라가는 로직까지 모두 구현했다. 즉 Iterative DFS 로도 기존 Recursive DFS 와 동일한 로직을 만든것이다. 만약 Recursive DFS에서 외부에서 로직을 수행한 것이 있다면 Iterative DFS 에서는 if문 내부에서 그 로직을 동일하게 수행해주면 된다. 이는 위에서 Iterative vs. Recursive 비교에서 제시한 코드를 통해서 알 수 있다. 또한 다음 포스팅에서 해당 방식을 사용하여 문제를 풀었기 때문에 이 과정을 더 상세히 확인할 수 있다.

결론

위 방식 말고도 Iterative DFS 를 구현하는 방법이 몇 가지 더 있다. 가령 for 문에서 break를 걸어주어 탈출 후 해당 노드가 리프인지 아닌지를 따로 검사해 탐색하는 방법이 있다. (궁금하다면 아래 2번째 링크를 참고하자)

그러나 위 방식 이외의 방법으로 Recursive와 동일한 로직을 내부에 구현해내기가 매우 까다로웠고, 또 구현했다고 하더라도 break를 활용하는 Iterative의 경우엔 또 다시 런타임 에러가 발생했다. 관련해서 분석을 좀 해 보았지만 런타임 에러가 발생하는 특정 경우만 찾았을 뿐 원인은 좀처럼 찾을 수 없었다.

때문에 현재까지는 위 방식이 가장 베스트 케이스인 것 같다. 위의 로직을 동일하게 요구하는 문제가 프로그래머스 Lv.4 [카카오 인턴] 동굴탐험 문제가 있다. 똑같이 리프노드에서 DFS 탐색을 통해 부모노드로 연산값을 전달하여 풀이할 수 있는데 주어진 n값이 최대 20만이고 역시 기대를 저버리지 않고 런타임 에러가 터진다. 언젠가 포스팅하겠지만 그 전에 위에서 구현한 Iterative DFS 방식을 가지고 구현할 것을 추천한다.

아이러니한점은 똑같이 Lv.4 [2021 KAKAO BLIND RECRUITMENT] 매출 하락 최소화 문제는 주어지는 n 값이 최대 30만인데, Recursive DFS 방식으로 정상 통과했다. 테스트 케이스에 30만이 다 주어지는 경우가 없었던 건지, 아니면 내가 모르는 또 다른 요인이 있는 것인지는 아쉽지만 밝혀내지 못했다. 관련해서 알고 있는 점이 있다면 댓글로 공유를 부탁드린다.

참고

  1. https://www.geeksforgeeks.org/iterative-depth-first-traversal/
  2. https://velog.io/@choiiis/%EC%9E%AC%EA%B7%80%ED%95%A8%EC%88%98-stack%EC%9D%84-%EC%9D%B4%EC%9A%A9%ED%95%9C-DFS-%EA%B8%B0%EB%B3%B8-%EA%B5%AC%ED%98%84
  3. https://lemidia.github.io/algorithm/DFS-Implementation-stack/
profile
KG
개발잘하고싶다
이전 포스트

[자료구조] JS로 구현하는 HEAP

다음 포스트

[자료구조] JS로 구현하는 순열과 조합

2개의 댓글

comment-user-thumbnail
sun202x
2022년 8월 10일

좋은 내용 잘봤습니다. 왜 자바스크립트에서의 dfs 알고리즘 구현을 stack으로 했는지 궁금했는데, 해당 글에서 알게되었네요 :)

답글 달기
comment-user-thumbnail
JourniYoon
2022년 8월 14일

매번 피했던 개념인데 정리해주신 글 덕분에 dfs 재귀랑 스택구조로 구현할 때 차이점을 조금 이해했습니다. 좋은 글 공유해주셔서 감사합니다.

답글 달기