[프로그래머스] LV.3 길 찾기 게임 (JS)

KG·2021년 5월 6일
Lv.3순회알고리즘카카오프로그래머스
3

알고리즘

목록 보기
43/61
post-thumbnail

문제

전무로 승진한 라이언은 기분이 너무 좋아 프렌즈를 이끌고 특별 휴가를 가기로 했다.
내친김에 여행 계획까지 구상하던 라이언은 재미있는 게임을 생각해냈고 역시 전무로 승진할만한 인재라고 스스로에게 감탄했다.

라이언이 구상한(그리고 아마도 라이언만 즐거울만한) 게임은, 카카오 프렌즈를 두 팀으로 나누고, 각 팀이 같은 곳을 다른 순서로 방문하도록 해서 먼저 순회를 마친 팀이 승리하는 것이다.

그냥 지도를 주고 게임을 시작하면 재미가 덜해지므로, 라이언은 방문할 곳의 2차원 좌표 값을 구하고 각 장소를 이진트리의 노드가 되도록 구성한 후, 순회 방법을 힌트로 주어 각 팀이 스스로 경로를 찾도록 할 계획이다.

라이언은 아래와 같은 특별한 규칙으로 트리 노드들을 구성한다.

  • 트리를 구성하는 모든 노드의 x, y 좌표 값은 정수이다.
  • 모든 노드는 서로 다른 x값을 가진다.
  • 같은 레벨(level)에 있는 노드는 같은 y 좌표를 가진다.
  • 자식 노드의 y 값은 항상 부모 노드보다 작다.
  • 임의의 노드 V의 왼쪽 서브 트리(left subtree)에 있는 모든 노드의 x값은 V의 x값보다 작다.
  • 임의의 노드 V의 오른쪽 서브 트리(right subtree)에 있는 모든 노드의 x값은 V의 x값보다 크다.

다행히 두 팀 모두 머리를 모아 분석한 끝에 라이언의 의도를 간신히 알아차렸다.

그러나 여전히 문제는 남아있다. 노드의 수가 예시처럼 적다면 쉽게 해결할 수 있겠지만, 예상대로 라이언은 그렇게 할 생각이 전혀 없었다.

이제 당신이 나설 때가 되었다.

곤경에 빠진 카카오 프렌즈를 위해 이진트리를 구성하는 노드들의 좌표가 담긴 배열 nodeinfo가 매개변수로 주어질 때,
노드들로 구성된 이진트리를 전위 순회, 후위 순회한 결과를 2차원 배열에 순서대로 담아 return 하도록 solution 함수를 완성하자.

제한

  • nodeinfo는 이진트리를 구성하는 각 노드의 좌표가 1번 노드부터 순서대로 들어있는 2차원 배열이다.
    • nodeinfo의 길이는 1 이상 10,000 이하이다.
    • nodeinfo[i] 는 i + 1번 노드의 좌표이며, [x축 좌표, y축 좌표] 순으로 들어있다.
    • 모든 노드의 좌표 값은 0 이상 100,000 이하인 정수이다.
    • 트리의 깊이가 1,000 이하인 경우만 입력으로 주어진다.
    • 모든 노드의 좌표는 문제에 주어진 규칙을 따르며,
    • 잘못된 노드 위치가 주어지는 경우는 없다.

입출력 예시

nodeinforesult
[[5,3],[11,5],[13,3],[3,5],[6,1],[1,3],[8,6],[7,2],[2,2]][[7,4,6,9,1,8,5,2,3],[9,6,5,8,1,4,3,2,7]]

풀이

2019 카카오 블라인드 테스트에서 출제된 문제이다. 지문이 복잡해 보이지만 요구하는 바는 상당히 간단하다. 자료구조 혹은 알고리즘 시간에 한번쯤은 접해봤을 법한 이진 트리의 순회 결과를 리턴하는 문제이다. 이진트리의 순회 방법은 크게 3가지로 분류할 수 있다.

  1. 전위순회 (Preorder Traversal)
    • root -> left -> right 순으로 탐색한다.
  2. 중위순회 (Inorder Traversal)
    • left -> root -> right 순으로 탐색한다.
  3. 후위순회 (Postorder Traversal)
    • left -> right -> root 순으로 탐색한다.

문제에서 요구하는 순회는 전위순회와 후위순회 2가지이다. 따라서 주어진 이진트리를 두 가지 방법으로 순회한 결과를 리턴할 수 있도록 구현하자.

이진트리 생성

먼저 주어진 nodeinfo의 정보를 토대로 이진트리를 만들어 줄 필요가 있다. 이를 위해서 nodeinfo를 재가공 하도록 하자. 보통 이진트리의 경우에는 노드의 값을 기준으로 큰 값과 작은 값을 구분하여 형성한다. 하지만 해당 문제에서는 값의 크기가 기준이 아닌, [x축 좌표, y축 좌표]로 부모-자식 관계를 형성해야 한다. 다음 이미지를 살펴보자.

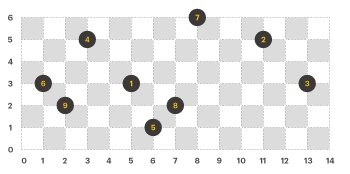
만약 nodeinfo에 따라 위와 같이 평면좌표에 각 노드가 그려지게 된다면, 이들 간의 부모-자식 관계는 아래의 이미지와 같다.

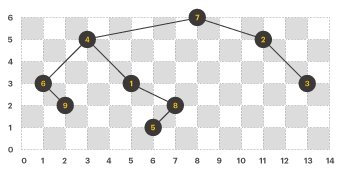
따라서 우리는 다음과 같은 사실을 알 수 있다. 이는 문제에서 설명된 조건을 다시 요약한 것과 동일하다.

  1. y축 좌표가 같다면 동일 레벨의 노드, 즉 형제노드이다.
  2. y축 좌표가 큰 값이면 부모, 작은 값이면 자식에 해당한다.
  3. 부모노드는 자신보다 작은 y축 좌표 중에 가장 가까운 노드 최대 두개를 자식노드로 삼을 수 있다.
  4. 부모노드의 x축 좌표보다 작은 노드는 왼쪽 자식노드, 큰 노드는 오른쪽 자식노드가 될 수 있다.

그렇다면 주어진 nodeinfo를 root부터 나열하기 위해서는 y축 좌표를 기준으로 내림차순 정렬을 실시하면 될 것이다. 그리고 정렬된 값을 기준으로 다시 x축 좌표를 기준으로 왼쪽과 오른쪽 노드를 구분하도록 삽입하여 이진트리를 생성해줄 수 있을 것이다.

먼저 nodeinfo를 y축 좌표 기준으로 내림차순 정렬을 해주자. 이때 반환값으로는 [노드번호, x축 좌표, y축 좌표]를 리턴하도록 했다. 노드번호의 1부터 시작하기 때문에 인덱스 값에 +1을 해야함에 주의하자.

// nodes는 y축을 기준으로 [ 노드번호, x좌표, y좌표 ]
// 순서로 내림차순 정렬된 결과를 할당받는다.
const nodes = nodeinfo.map((node, idx) => [ idx+1, node[0], node[1] ])
		      .sort((a, b) => b[2] - a[2]);

다음은 nodes를 가지고 이진트리를 만들어주도록 하자. 자바스크립트도 ES6를 기점으로 다른 객체지향언어처럼 class 문법을 사용할 수 있다. 따라서 이진트리를 클래스를 이용하여 만들어주자.

ES6 이전에는 prototype 속성을 이용해 클래스 기능을 구현했었다.

해당 클래스의 생성자 constructor는 특정 노드의 정보를 전달받아 해당 노드를 생성하도록 설계하자. 노드번호와 x좌표를 전달받아 노드 생성을 해주면 될 것이다. 또한 왼쪽과 오른쪽에 자식 노드가 들어갈 수 있기 때문에 해당 값을 초기에 null로 초기화해주자. 들어갈 수도 있지만 들어오지 않을 수도 있기 때문이다.

class BinaryTree {
  // value와 x_pos를 전달받아 프로퍼티(property)값으로 초기화
  constructor(value, x_pos) {
    this.value = value;
    this.x_pos = x_pos;
    this.left = null;
    this.right = null;
  }
}

특정노드는 해당 이진트리의 root 노드가 될 것이다. 즉 nodes의 가장 첫 원소의 정보를 넘겨주어 생성하면 될 것 이다. 이후 left와 right에는 root의 자식이 될 노드들을 x축 좌표로 구분하여 넣어주도록 하자. nodes는 이미 y축을 기준으로 정렬되어 있기 때문에 항상 이전의 노드보다 y축 값이 같거나 작다. 이때 root 노드는 항상 하나만 존재하기 때문에 이후에 들어오는 노드는 항상 root 노드의 자식 -> 손자 -> ... 의 관계일 수 밖에 없다. 따라서 단순히 x축 좌표만 가지고 왼쪽 자식일 지, 오른쪽 자식일 지 구분해줄 수 있다.

class BinaryTree {
  constructor(value, x_pos) {
    ...
  }
  
  // 입력받은 x좌표와 현재 부모노드의 x좌표를 비교하여
  // 작거나 같은 경우 왼쪽 자식노드로,
  // 큰 경우엔 오른쪽 자신도느로 보낸다.
  insert(value, x_pos) {
    x_pos <= this.x_pos
    	? this._toLeft(value, x_pos);
    	: this._toRight(value, x_pos);
  }
}

위 insert 메소드에서 왼쪽과 오른쪽으로 자식을 배치하는 _toLeft와 _toRight 메서드를 각각 구현해주자. 삽입의 경우는 이진트리에서의 새로운 값 삽입과 마찬가지로 root 노드부터 그 값을 비교하여 위치를 찾게 된다. 따라서 왼쪽노드가 비어있는 경우(= null)라면 새로 이진트리의 노드를 생성하여 할당해주고, 이미 할당된 노드가 있으면 해당 노드에서 다시 insert 메서드를 호출하여 내려가도록 설계해주자.

class BinaryTree {
  constructor(value, x_pos) { 
    ... 
  }
    
  insert(value, x_pos) {
    ...
  }
    
  // 이미 왼쪽자식이 있다면 다시 insert 메서드 호출
  // 그 외의 경우 해당 노드 정보가 왼쪽 노드가 됨
  _toLeft(value, x_pos) {
    this.left
    	? this.left.insert(value, x_pos)
    	: this.left = new BinaryTree(value, x_pos);
  }
    
  // 이미 오른쪽자식이 있다면 다시 insert 메서드 호출
  // 그 외의 경우 해당 노드 정보가 오른쪽 노드가 됨
  _toRight(value, x_pos) {
    this.right
    	? this.right.insert(value, x_pos)
    	: this.right = new BinaryTree(value, x_pos);
  }
}

해당 클래스를 이용하여 다음과 같이 최종적으로 이진트리를 만들어줄 수 있다.

// 첫 원소가 root 이므로 해당 노드의 번호와 x좌표 전달
const bTree = new BinaryTree(nodes[0][0], nodes[0][1]);
// 다음 원소부터 차례로 insert 메서드 호출
for(let i = 1; i < nodes.length; i++) {
  bTree.insert(nodes[i][0], nodes[i][1]);
}

Preorder 및 Postorder 구현

이 부분 역시 이진트리를 이미 생성해두었으므로 여타 다른 이진트리에서의 전위와 후위순회와 동일한 방식으로 구현해주면 된다. 보통 순회는 재귀적으로 구현을 하고, Tree의 깊이 역시 조건에 의해 최대 1000 이하이므로 자바스크립트에서도 재귀적으로 구현해도 스택 오버플로우가 일어날 확률이 낮다. 따라서 두 함수를 재귀적으로 구현해보자.

전위 순회(Preorder)의 경우는 root -> left -> right 순서로 탐색을 진행한다. 이는 root노드를 선방문 후 왼쪽 자식 노드를 다시 root로 삼아 하나의 서브트리를 만들고 해당 매커니즘을 반복한다. 왼쪽 서브트리에서 모든 방문이 끝나면 오른쪽 자식 역시 이를 동일하게 반복하게 된다. 따라서 다음과 같이 재귀적으로 구현해 줄 수 있다.

// arr 은 문제에서 방문한 노드의 순서를 배열 형태로
// 리턴해야 하기때문에 이를 저장하기 위한 배열이다.
const preorder = (bTree, arr) => {
  // 재귀적으로 호출되며 전달된 현재 이진 트리의 노드가
  // 비어있지 않을 경우 계속 탐색 (비어있다면 탈출조건이 됨)
  if(bTree !== null) {
    // 루트를 가장 먼저 탐색 (푸시)
    arr.push(bTree.value);
    // 그리고 왼쪽 -> 오른쪽 순서로 재귀호출 진행
    preorder(bTree.left, arr);
    preorder(bTree.right, arr);
  }
}

후위 순회(Postorder) 역시 위와 동일한 매커니즘을 구현이 가능하다. 이번엔 left -> right -> root 순서로 탐색하도록 다음과 같이 재귀적으로 구현해주자. 

const postorder = (bTree, arr) => {
  if(bTree !== null) {
    // 왼쪽 -> 오른쪽 순서로 재귀호출 진행
    postorder(bTree.left, arr);
    postorder(bTree.right, arr);
    // 그리고 마지막으로 루트노드 방문
    arr.push(bTree.value);
  }
}

그리고 해당 함수를 메인 함수에서 호출하여 방문 순서를 담은 배열을 리턴해주자.

// 각 순회 결과를 저장할 배열 선언
const preorderArr = [];
const postorderArr = [];

...

preorder(bTree, preorderArr);
postorder(bTree, postorderArr);

return [preorderArr, postorderArr];

전체코드

이진트리에 대한 기본 개념을 묻는 문제인만큼 이진 트리를 구현할 줄 알고, 이에 대한 순회 개념을 잘 알고 있었다면 쉽게 구현할 수 있는 문제였던 것 같다. 노드의 값이 아닌 x좌표로 왼쪽과 오른쪽 자식을 구분해야 하는것만 주의해서 구현하면 크게 어려움이 없다. 물론 코딩테스트에서 인터넷 검색이 불가했고 어렴풋이 개념만 약간 알고 있었다면 실제 구현에 꽤나 어려움이 많았을 것으로 예상된다. 중위순회(Inorder)를 제외한 이유는 나름의 난이도조절의 배려였을까? 주석을 제외한 전체 코드는 다음과 같다.

function solution (nodeinfo) {
  const preorderArr = [];
  const postorderArr = [];
  
  const nodes = nodeinfo.map((node, idx) => [ idx+1, node[0], node[1] ])
  			.sort((a, b) => b[2] - a[2]);
  
  const bTree = new BinaryTree(nodes[0][0], nodes[0][1]);
  for(let i = 1; i < nodes.length; i++) {
    bTree.insert(nodes[i][0], nodes[i][1]);
  }
  
  preorder(bTree, preorderArr);
  postorder(bTree, postorderArr);
  
  return [preorderArr, postorderArr];
}

class BinaryTree {
  constructor(value, x_pos) {
    this.value = value;
    this.x_pos = x_pos;
    this.left = null;
    this.right = null;
  }
  
  insert(value, x_pos) {
    this.x_pos >= x_pos
    	? this._toLeft(value, x_pos)
    	: this._toRight(value, x_pos);
  }
  
  _toLeft(value, x_pos) {
    this.left 
    	? this.left.insert(value, x_pos)
    	: this.left = new BinaryTree(value, x_pos);
  }
  
  _toRight(value, x_pos) {
    this.right
    	? this.right.insert(value, x_pos)
    	: this.right = new BinaryTree(value, x_pos);
  }
}

const preorder = (bTree, arr) => {
  if(bTree !== null) {
    arr.push(bTree.value);
    preorder(bTree.left, arr);
    preorder(bTree.right, arr);
  }
}

const postorder = (bTree, arr) => {
  if(bTree !== null) {
    postorder(bTree.left, arr);
    postorder(bTree.right, arr);
    arr.push(bTree.value);
  }
}

출처

https://programmers.co.kr/learn/courses/30/lessons/42892

profile
KG
개발잘하고싶다
이전 포스트

[프로그래머스] LV.3 경주로 건설 (JS)

다음 포스트

[프로그래머스] LV.3 징검다리 건너기 (JS)

0개의 댓글