문제
하노이 탑(Tower of Hanoi)은 퍼즐의 일종입니다. 세 개의 기둥과 이 기동에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있습니다. 게임의 목적은 다음 두 가지 조건을 만족시키면서, 한 기둥에 꽂힌 원판들을 그 순서 그대로 다른 기둥으로 옮겨서 다시 쌓는 것입니다.
- 한 번에 하나의 원판만 옮길 수 있습니다.
- 큰 원판이 작은 원판 위에 있어서는 안됩니다.
하노이 탑의 세 개의 기둥을 왼쪽 부터 1번, 2번, 3번이라고 하겠습니다. 1번에는 n개의 원판이 있고 이 n개의 원판을 3번 원판으로 최소 횟수로 옮기려고 합니다.
1번 기둥에 있는 원판의 개수 n이 매개변수로 주어질 때, n개의 원판을 3번 원판으로 최소로 옮기는 방법을 return하는 solution를 완성해주세요.
제한
- n은 15이하의 자연수 입니다.
입출력 예시
| n | result |
|---|---|
| 2 | [ [1,2], [1,3], [2,3] ] |
풀이
재귀함수 풀이의 대표적인 문제인 하노이의 탑이다. 개발에 입문하기 전에도 많이 접해보는 문제이기도 하다. 재귀 함수는 나 자신을 호출하여 로직을 수행하는 구조이기 때문에 LIFO(Last In First Out) 구조의 스택과 그 흐름이 유사한 점이 많다. 때문에 재귀 함수는 스택을 활용하거나 반복문을 통해 구현하는 식으로도 바꾸어 줄 수 있다. 재귀 함수의 효율성 개선을 위해 이런 식으로 구현을 하는 것으로는 DP(Dynamic Programming)이 있다. 그 밖에도 꼬리재귀(Tail Recursion)와 같은 최적화 기법도 있지만 해당 주제는 다른 포스팅에서 더 자세히 다뤄보기로 하자.
그러나 모든 재귀함수가 위와 같이 스택이나 반복문의 구조로 변경할 수 있는 것은 아니거나 변환이 가능하다고 하더라도 재귀보다 그 구조가 복잡해질 가능성이 있다. 해당 문제에서는 주어진 n값이 최대 15로 크지 않기 때문에 스택 오버플로우(Stack Overflow)에 대한 염려가 없어 간편하게 재귀로 풀이하겠다.
하노이의 탑은 이미지를 보면서 설명하는 것이 좋을 것 같다. 프로그래머스 문제에 첨부된 이미지를 함께 보며 풀어보자. 일단 기본 조건을 인지하고 있어야 하는데, 한 번에 하나의 원판만 옮길 수 있다는 점과 큰 원판은 작은 원판 위에 올라설 수 없다는 것이 중요하다.
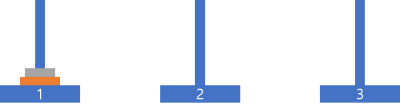
(1) 초기 상태는 항상 위 그림과 같이 1번 기둥에 모든 원판이 모여있다. 여기서 우리가 옮길 수 있는 원판은 가장 상위에 있는 원판이다. 최종 목적은 1번 기둥에 있는 모양 그대로 3번 기둥으로 보내는 것이기 때문에 가장 상판에 있는 원판을 2번 기둥에 잠깐 옮겨둔다.
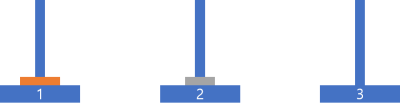
(2) 1번 기둥에 남아있는 원판은 가장 큰 원판이기 때문에 바로 종착지인 3번 기둥으로 옮겨갈 수 있다.
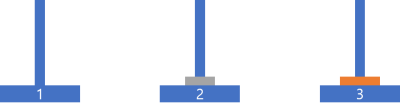
(3) 경유지인 2번 기둥에 있는 원판은 3번 기둥에 있는 원판보다 더 작기 때문에 옮겨 갈 수 있다.
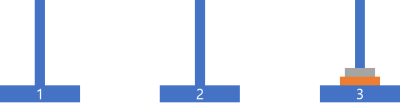
(4) 모든 원판의 이동이 성공적으로 완료되었다.
단 두개의 원판만 있었기에 다음의 과정으로 모든 원판의 이동이 끝나게 되었다. 그러나 원판이 많아지게 되면 과정이 길어지게 될 것이다. 그렇지만 과정이 길어진다고 하더라도 위의 원칙은 변하지 않는다. 어떤 식으로 재귀적으로 접근할 수 있는지 살펴보자.
먼저 (1)번 과정에서 우리는 가장 상판의 원판을 경유지로 옮기게 되었다. 왜냐하면 한 번에 하나의 원판만을 옮길 수 있기 때문이다. 이때 가장 밑에 있는 원판은 제일 크기가 큰 원판이기 때문에 최종적으로는 3번 기둥에서도 가장 밑에 위치해야 할 것 이다. 즉 가장 밑에 있는 원판을 n번째 원판이라고 할 때, 해당 원판이 3번 기둥의 가장 밑에 위치하기 위해서는 n-1 번째까지의 모든 원판이 2번 기둥에 위치해야 할 것 이다. 이때 모든 원판을 한 번에 옮길 수는 없기 때문에 경유하는 기둥을 한 번씩 거쳐서 이동하도록 해주어야 한다. hanoi라는 함수를 만들고 매개변수로 (원판, 시작위치, 도착위치, 경유위치)를 입력받을때 다음처럼 선언할 수 있다.
-
hanoi(n-1, start, end, via)- n-1개의 원판을 start에서 end를 거쳐 via로 이동
위의 과정이 완료되면 1번 기둥에는 n번째 원판만 남아있는 상태가 될 것이다. 그렇다면 우리는 해당 원판을 바로 1번에서 3번 기둥으로 옮겨 줄 수 있다.
move start -> end
나머지 n-1개의 원판은 아직 2번 기둥에 남아있다. 이때 2번 기둥에 있는 모든 원판들의 크기는 3번 기둥에 위치한 원판보다 그 크기가 작다. 따라서 n-1개의 원판 모두 2번 기둥에서 3번 기둥으로 올라갈 수 있다. 역시 모든 원판을 한 번에 옮길 수 없기 때문에 비어있는 경유 기둥인 1번을 이용하여 모두 3번으로 옮겨줄 수 있다. 따라서 다음처럼 선언할 수 있다.
-
hanoi(n-1, via, start, end)- n-1개의 원판을 via에서 start를 거쳐 end로 이동
위의 3개의 과정이 hanoi라는 함수에서 재귀적으로 계속 호출될 것이다. 왜냐하면 크기가 1씩 작아질 뿐 모든 원판의 이동 방법은 공통되기 때문에 똑같은 로직을 적용할 수 있는 것이다. 재귀함수에서 가장 중요한 탈출 조건은 다음과 같다. n이 1이 되는 순간은 바로 시작위치에서 도착위치로 옮겨줄 수 있기 때문에 이를 반환하도록 하면 된다. 해당 문제에서 정답으로 요구하는 것이 위 과정의 순서를 담은 배열이기 때문에, 우리는 탈출조건과 위 2번의 과정에서 배열에 시작위치에서 도착위치로 옮겨가는 원판을 담아주면 된다.
하노이의 탑은 유명한 문제이고 다른 블로그에서도 상세히 그림과 함께 설명된 부분이 많아 간단하게 살펴보았다. 이해가 잘 가지 않는다면 다른 블르고 글을 함께 보는 것을 추천한다. 다음은 전체코드이다. 위 설명된 방식에서 배열을 저장할 매개변수 하나를 추가했다.
코드
function solution(n) {
const answer = [];
hanoi(n, 1, 2, 3, answer);
return answer;
}
const hanoi = (n, start, via, end, answer) => {
if(n === 1) answer.push([start, end]);
else {
hanoi(n-1, start, end, via, answer);
answer.push([start, end]);
hanoi(n-1, via, start, end, answer);
}
}
