
소수(Prime number)
2, 3, 5, 7, 11, 13, 17 ...처럼
- 1과 자기 자신만으로 나누어 떨어지는 1보다 큰 양의 정수
-1은 소수가 아니다.
-음수는 소수가 아니다.- n이 소수가 되려면 2보다 크거나 같고, n보다 작은 자연수로 떨어지면 안된다.
그렇다면 우리는 어떻게 소수를 구할 수 있을까?
반복문만 사용하기
첫번째로는 반복문을 사용하여 소수를 구하는 방법이 있을 것이다.
// 방법1
function isPrime(num) {
// 소수는 1과 자기 자신만으로만 나누어 떨어지는 수 임으로
// num > i
for(let i = 2; num > i; i++) {
if(num % i === 0) { //이 부분에서 num이 다른 수로 나눠떨어진다면 소수가 아님
return false;
}
}
// 소수는 1보다 큰 정수임으로
// 1보다 작으면 false를 리턴한다
return num > 1;
}제곱근 Math.sqrt()
- n이 소수가 아닐 때
N = a*b
- n이 소수일 때 (1과 자신만을 약수로 가짐으로)
a와 b의 관계식은 a <= b 이다.
(만약 a > b 이면 두 수를 바꿔서 b <= a 라고 표현할 수 있다.)
a와 b의 차이가 최소로 날 때 그 값은 √n*√n = n 이 나온다.
따라서 n이 axb로 표현될 수 있고, a <= b일 때, b의 최소값이며 a의 최대값은 √n이다.
- a가 √n보다 크게 되면, a*b > n
- b가 √n보다 작게 되면, a*b < n
- 따라서 a <= b일 때, a <= √n, b >=√n이다.
a와 b의 차이가 가장 작은 경우는 a와 b가 서로 √n이 되는 경우이다. 그러므로 √n까지만 반복해보면 이 수가 소수인지 알 수 있다.
위의 말을 예를 들어 쉽게 설명하자면 다음과 같다.
n = 36이라고 가정해보자.
36의 약수는 1, 2, 3, 4, 6, 9, 12, 18, 36 이다.
이는 1x36, 2x18, 3x12, 4x9, 6x6의 결과이다.
이들은 반비례 관계로 몫이 커지면 나누는 값이 작아지거나, 나누는 값이 커지면 몫이 작아진다. n의 절반(제곱근)까지 계산하게 되면 이후 몫과 나누는 값은 반대로 바뀐다.
- 따라서 n의 제곱근까지, 그러니까 a와 b가 서로 √n이 될 때 까지만 반복해보면 이 수가 소수인지 알 수 있다.
단, 제곱근으로 구할 시 3, 5, 7의 제곱근은 " Math.sqrt(9) = 3" 보다 더 작다는 것을 염두해 두어야 한다.
// 방법2
function isPrime(num) {
if(num <= 1) { // 음수와 1은 소수가 아니다
return false;
}
// 2는 짝수 중 유일한 소수이다
if( num % 2 === 0) {
return num === 2 ? true : false;
}
// 이제 num이 홀수 일때 다른 수에 나눠지는지 판별한다
// Math.sqrt(num) 즉, √num까지 나눠 떨어지는지 검사한다
// 원리는 아래글 "에라토스테네스의 체" 참고
const sqrt = parseInt(Math.sqrt(num));
for( let divider = 3; divider <= sqrt; divider += 2) {
if(num % divider === 0) {
return false;
}
}
return true;
}에라토스테네스의 체
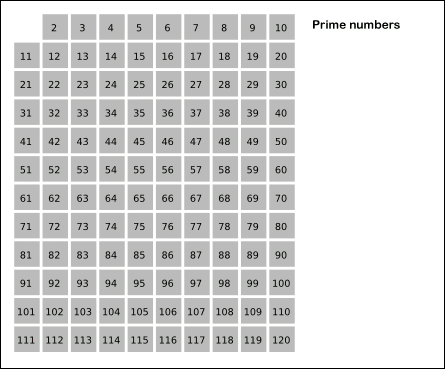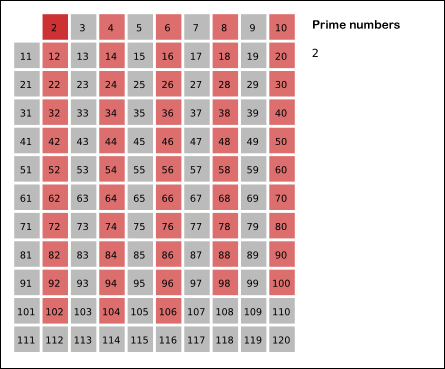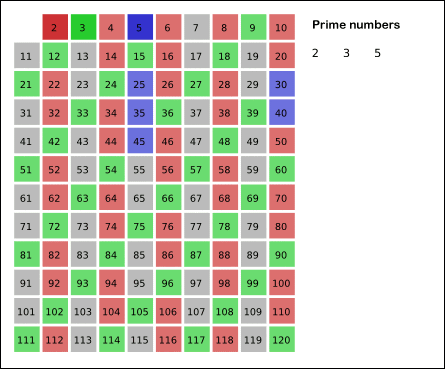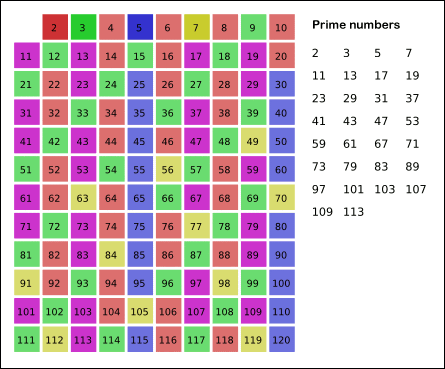
1을 제외하고 2부터 N까지 자신을 제외하고 순차적으로 자신의 배수들을 지워가면 결국에는 소수들만 남는다는 원리이다. n까지가 아니라 √n까지만 검사해도 결과는 같다.
예를 들어 N = 25 이라고 가정해보자.
- 1은 소수가 아니기 때문에 2부터 실행한다.
- 2를 제외하고 2의 배수를 모두 제거한다. [4,6,8,10,12,14,16,18,20...제거]
- 3을 제외하고 3의 배수를 모두 제거한다. [9,15,21,24...제거] _6,18... 등은 2의 배수에서 이미 제거됨
- 4는 이미 삭제되었다.
- 5를 제외하고 5의 배수를 모두 제거한다[25,35,45,55... 제거]____(5의 제곱이 나오기 전까지 모든 5의 배수는 이미 삭제되었다)
- 6은 이미 삭제되었다.
따라서 √25(5)까지만 검사하면 된다. √25(5)이후의 배수들은 이미 삭제되었기 때문이다.
(여기서 n은 25라 가정 , 1부터 25까지의 5의 배수는 25를 제외하고 이미 지워진 상태이다 )
9개의 댓글
안녕하세요
본문에 작성해주신 글 잘 봤습니다.
글을 다 읽고 궁금한 점이 있어 댓글을 남깁니다!
-
방법2에서 parseInt을 사용해 소수점을 버리는 이유가 무엇인가요?
파라미터로 받은 num은 얼리리턴을 해줄때 number 타입인 1, 3, 5, 7 혹은 % 2 ===0과 같이 체크를 합니다.
하지만 parseInt는 문자열을 정수로 return 해주는 함수인데 Math.floor가 아닌 parseInt를 사용하신 이유가 있을까요? -
방법2에 isPrime 함수에 for문안에 return true가 있어 2회 이상 반복이 되지않습니다.
return true는 for문 안이 아닌 isPrime scope 최하단에 위치해있는게 맞을 것 같습니다.





안녕하세요.
본문에 있는 함수 isPrime()으로는 제곱근이 3보다 작은 홀수 3, 5, 7 에서 undefined를 반환하기 때문에 소수 판별 함수로 보기 어렵습니다.