BOJ 21314 - 민겸 수 (Python)

S1, 구현

문제

민겸이는 로마 숫자를 보고 굉장히 흥미롭다고 생각했다. 그래서 민겸이는 새로운 수 체계인 민겸 수를 창조했다.
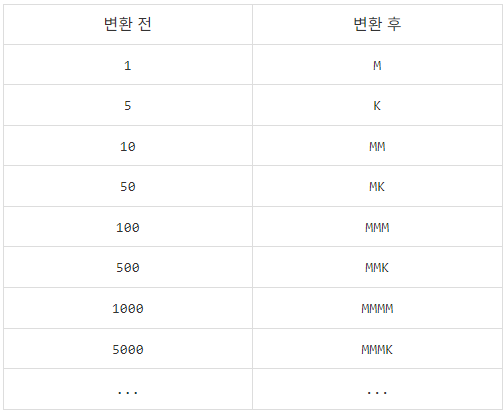
민겸 숫자는 0 이상의 정수 N에 대해 10^N 또는 5 × 10^N 꼴의 십진수를 대문자 M과 K로 이루어진 문자열로 표기한다. 10^N 꼴의 십진수는 N + 1개의 M으로, 5 × 10^N 꼴의 십진수는 N개의 M 뒤에 1개의 K를 이어붙인 문자열로 나타낸다. 즉, 아래 표처럼 나타낼 수 있다.

민겸 수는 한 개 이상의 민겸 숫자를 이어붙여 만든다. 예를 들어, 민겸 수 MKKMMK는 MK, K, MMK의 세 민겸 숫자를 이어붙여 만들 수 있다.

민겸 수를 십진수로 변환할 때는, 1개 이상의 민겸 숫자로 문자열을 분리한 뒤, 각각의 민겸 숫자를 십진수로 변환해서 순서대로 이어붙이면 된다. 민겸 숫자를 십진수로 변환하는 것은 십진수를 민겸 숫자로 변환하는 과정을 거꾸로 하면 된다. 예를 들어, 민겸 수 MKKMMK는 아래 그림과 같이 여러 가지 십진수로 변환할 수 있다.

민겸이는 위와 같이 하나의 민겸 수가 다양한 십진수로 변환될 수 있다는 사실을 알았다. 문득 민겸이는 변환될 수 있는 십진수 중 가장 큰 값과 가장 작은 값이 궁금해졌다. 민겸이를 위해 하나의 민겸 수가 십진수로 변환되었을 때 가질 수 있는 최댓값과 최솟값을 구해주자.

풀이

• 주어진 문자열을 탐색하며 M 일때는 cnt을 올려주고, K일때는 cnt를 통해 값을 계산해주는 문제
• 유의해야 할 점은 MMKMM 처럼, M으로 끝나는 경우를 생각하는 것이다.

# S1, 민겸 수
minkum = input().rstrip()
minValue = ""
maxValue = ""

cnt = 0
for w in minkum:
    if w == 'M':
        cnt += 1
    else:
        if cnt == 0:
            minValue += '5'
            maxValue += '5'
            continue
        else:
            # 앞에 n개의 M이 있고 K로 끝남
            
            maxtmp = 5 * (10**cnt)
            mintmp = 10**(cnt - 1)

            minValue += str(mintmp)
            minValue += '5'
            
            maxValue += str(maxtmp)
        
            cnt = 0

if cnt > 0:
    maxtmp = '1' * cnt
    mintmp = 10**(cnt - 1)
	
    # MMM의 경우, 최대는 111, 최소는 100
    maxValue += str(maxtmp)
    minValue += str(mintmp)

print(maxValue)
print(minValue)