[빅데이터분석기사] Part3 - CH 02. 분석 기법 적용 (1)

Chapter 02. 분석 기법 적용

---

Section 01. 분석기법

1. 분석기법 개요

1-1. 지도 학습

• 정답이 있는 데이터(Labelled Data)로 학습
  : Training Dataset / Test Dataset

  1. Classification
     : Decision Tree , Random Forest, ANN, SVM 등
     1-1. 이진 분류 : Logisitic Regression
     1-2. 다중분류
     
  2. Regression
     : 주어진 데이터 기반해 새로운 값 예측
     : Decision Tree, Linear Regression, Multiple Regression

1-2. 비지도 학습

• 정답이 없는 데이터 학습해 숨겨진 의미/패턴 도출 및 구체화
• 학습 모델 성능 평가 어려움
• Clustering, Neural Network, Auto Encoder

1-3. 준지도 학습

• Labelled, Unlabelled 동시 학습
• 소수의 Labelled Data로 학습된 부분 학습 모델을 통해 나머지 데이터에 라벨 생성 후 지도 학습 수행
• Self-Training, GAN

1-4. 강화 학습

• 주어진 환경에서 보상 최대화
• Q-Learning, 정책 경사(PG)

---

2. 회귀 분석

• 특정 변수가 다른 변수에 어떤 영향을 미치는 지에 대한 수학적 설명/예측
  • 독립변수를 통한 종속변수 예측
• 회귀선(회귀계수) : 독립변수에 대한 종속변수의 기대값, 최소제곱법 사용

  최소제곱법
  : 잔차 제곱의 합이 최소가 되게 하는 직선을 의미

  • 잔차 : 실제 값과 예측 값의 차이

회귀 분석 모형 진단

1. 적합도 검정
   : 추정된 회귀식이 표본의 실제값을 설명하는 정도
   : R^2 (결정계수)를 알고있다는 가정 하에,
   SSR(회귀제곱합) / SST(총제곱합), 1에 가까울 수록 설명력↑

2. 변수영향력 분석
   : p < 0.05 = 통계적 유의미

2-1. 선형 회귀 분석 : Linear Regression

• 종속변수 Y와 1개 이상의 독립변수 X와의 선형 상관성
• X, Y 모두 연속형 변수
• 잔차의 기대값은 0, 정규분포를 이뤄야 함
  : 잔차는 서로 독립 & 분산 일정

1. 단순 선형 회귀 분석

• X 1개, Y 1개
• y = ax + b (a : 회귀 계수, b: 절편)

2. 다중 선형 회귀 분석

• X 多, Y 1개
• y = ax1 + bx2 + ... + c

3. 일반화 선형 모델 (GLM)

• 종속변수 Y가 정규 분포를 따르지 않아도 적용 가능

• 선형 예측 변수 + 링크 함수를 통해 Y와의 관계 설명

• 선형 회귀, 로지스틱 회귀, 포아송 회귀 등

  선형 예측 변수
  : 독립변수 + 모수(Parameter)

  링크 함수
  : 선형 예측 변수와 종속변수 간 관계를 표현하는 함수

• GLM은 종속변수가 특정확률분포(이항분포, 포아송분포 등)를 따른다고 가정

2-2. 로지스틱 회귀 분석 : Logistic Regression

• 종속변수가 이항분포를 따르는 범주형 변수

1. 단순 로지스틱

: 종속변수 = 이항형(2개 범주)

2. 다중 로지스틱

: 종속변수의 범주가 2개 이상

로지스틱 회귀함수식
: 각 모수(Parameter)에 대해 비선형
: 승산(odds)로 로짓 변환 ▶ 0~1로 조정해 선형함수로 치환

• 승산
  : 사건A가 발생하지 않을 확률 대비 일어날 확률의 비
  : P(A) / 1-P(A)

---

3. 의사결정나무 : Decision Tree

• 전체 자료 → N개의 소집단 → Classification or Prediction 수행
• 상위 노드 → 하위 노드로 갈수록
  노드 내 동질성↑ & 노드 간 이질성↑

3-1. 구성

1. Root Node : 대상이 되는 모든 자료 집합
2. Internal Node : 중간 마디
3. Terminal Node : 끝 마디
4. Depth : 가장 긴 마디의 개수

3-2. 종류

1. 분류나무

• 이산형 목표변수 : 빈도 기반 입력 데이터
• 빈도 기반 분리

  분리 기준
  : 불순도(서로 다른 데이터의 섞임 정도)가 자식 노드로 갈수록 감소하도록

  • 정보 획득
    : 부모 자식 간의 불순도 차이(순도↑, 불확실성↓)

  1. 카이제곱 통계량의 p-value
  : ((실제도수-기대도수)^2 / 기대도수)의 합

  2. 지니 지수
  : 한 항목의 무작위 라벨 추정 시, 틀릴 확률

  3. 엔트로피 지수
  : 무질서 정도에 대한 측도

2. 회귀나무

• 연속형 목표변수 : 평균/표준편차 기반 예측 결과, 유의미한 실수 값
• 평균/표준편차 기반 분리

  분리 기준

  1. F-통계량의 p-value
  : 등분산성 검정, p-value ∝ 등분산성(순수도)

  2. 분산 감소량
  : 분산 감소량 ∝ 순수도

3-3. Decision Tree 분석 과정

1. 변수 선택
   : 목표 변수와 관련된 독립 변수 선정

2. Decision Tree 형성
   : 분리 기준, 정지 규칙, 평가 기준 수립

   정지 규칙
   : 더이상 분리되지 않을 노드에 대한 선정 규칙

   • Depth가 지정한 최대값 도달
   • Terminal Node의 샘플수가 최솟값에 도달
   • 불순도 감소가 더이상 진행되지 않음

3. 가지치기
   : 과적합 방지, 일반화 향상
   : 부적절 추론 규칙, 분류 오류 위험 마디 제거

   • 에러 감소 가지치기
     : 분할/결합 전과 오류 비교해, 오류 감소 전까지 반복
   • 룰포스트 가지치기
     : Root → Leaf 경로의 정확도 낮은 순으로 제거

4. 모형 평가 및 예측

   • 정보 획득
     : 순도 증가, 불확실성 감소
     : 현재 노드의 불순도 - 자식 노드의 불순도
     : 어떤 기준으로 분할하는 것이 순수성 증가에 도움을 주는지 판단

   • 재귀적 분기 학습
     : 분기 이후 순도 증가, 불확실성 감소 = 각 영역의 정보 획득량 증가
     : 모든 Terminal Node의 엔트로피 = 0

5. 타당성 평가

6. 해석 및 예측

3-4. Decision Tree 대표 알고리즘

1. CART

• 분류, 회귀 모두 적용 가능
• 데이터를 가장 잘 분할하는 기준을 반복적으로 찾아 트리 생성
  • 범주형, 이산형 변수 : 지니지수
  • 연속형 변수 : 분산감소량 기반 이진 분리
• 직관적, 이해 쉬움, 데이터 전처리 불필요
• 불안정성 높음, 과적합 가능성↑
  

2. C 4.5 / C 5.0

• Decision Tree 발전 형태
• 데이터 마이닝 알고리즘 중 사용↑
• 범주형, 이산형 변수에만 사용 가능
  • 불순도 측도로 엔트로피 지수 사용

3. CHAID

• 범주형, 이산형, 연속형 변수 모두 사용 가능
  • 불순도 측도로 카이제곱 통계량 사용
• Multiway split 허용
• 가지치기없이 적당한 크기에서 성장 중지 = 과적합 방지

4. Random Forest

• Bootstrapping기반 Sampling Decision Tree
  : Bagging 기반 앙상블 학습

• Bagging
  : 여러 부트스트랩 자료 생성 및 학습을 통한 분류기(Classifier)를 생성해
  결과를 앙상블
  : 모델 과적합 방지 & 예측에 대한 분산 감소
  : 각 샘플별 모델링 → 학습 → 결과 집계

  1. 범주형 변수 : 다수결 투표
  2. 연속형 변수 : 평균

Boosting
: 별개의 앙상블 기법 중 하나
: Weak Classifier에 가중치를 부여해 순차적으로 연결
: 모델의 bias를 줄이고, 새로운 분류 규칙 생성이 목표

• AdaBoost, GBM, XGBoost, Light GBM 등

3-5. Decision Tree 장단점

• 장점

1. 연속, 범주형 변수 모두 적용 가능
2. 변수에 대한 비교 가능
3. 규칙 이해가 쉽고, 데이터로부터 규칙 도출 유용

• 단점

1. 트리 구조의 복잡성 ∝ 예측력, 해석력
2. 데이터 변형에 민감함

---

4. 인공신경망 : Artifical Neural Network

4-1. 특징

• 입력 데이터 → 가중치 처리 → 활성화 함수 → 출력 계산 → 가중치 조정
  의 과정을 거침

• ANN 모형 구축 시 고려 사항

  • 범주형 변수 : 일정 빈도 이상 등장, 범주가 일정 구간 내
  • 연속형 변수 : 값들 간의 범위 차가 작아야 함 (for 표준화)

4-2. 발전 과정

1. 다층 퍼셉트론의 문제
   : vanishing gradient (신경망 층수 증가에 따른 기울기 소실 문제 발생)
   : 과적합

2. Deep Learning의 등장
   : pre-training을 통한 기울기 소실 문제 해결
   : 초기화 알고리즘, DropOut을 통한 과적합 방지
   : DNN = 2개 이상의 은닉층

   • CNN, RNN, LSTM, GAN, GRU, AutoEncoder

4-3. 원리

• 입력값X 에 대해 다음 뉴런으로의 적절한 출력값 생성해 목표값Y 도달

  • X * weights + bias → 학습 & 최적화 → 활성화 함수
  • 가중치(weights) : 노드와의 연결계수
  • 활성 함수 : 노드의 활성화 여부를 결정하는 임계값

• 뉴런 간 연결

  1. 층 간 연결 : 서로 다른 층의 뉴런 간 연결
  2. 층 내 연결 : 동일 층 내 뉴런 간 연결
  3. 순환 연결 : A 뉴런의 출력이 A에게 입력으로 돌아옴

4-4. 학습

• 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정
• 손실함수 값이 최소가 되게하는 가중치와 편향 도출

1. 손실 함수 : Loss Function

• 신경망 출력값과 실제값 사이의 차이를 즉정하는 함수
• 모델의 성능을 평가하는 척도
• 경사 하강법과 같은 최적화 알고리즘을 통해 손실 함수의 기울기 계산

2. 평균제곱오차 : MSE

• 가장 널리 사용되는 손실 함수
• 실제 값과 예측 값 차이의 제곱에 대한 평균
  

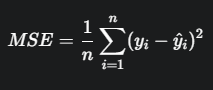
3. 교차엔트로피 오차 : CEE

• 예측한 확률 분포와 실제 확률 분포 간의 차이를 측정하는 손실 함수
• Classificaition 모델에 사용
• 모델이 잘못 예측했을 때 큰 penalty 부여

1. 이진 교차 엔트로피 : 이진 분류에 사용
   
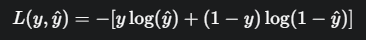
2. 다중 클래스 교차 엔트로피 : 다중 클래스 분류
   
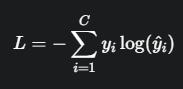
   여기서, C : 클래스 총 개수, yi : One-Hot Encoding Vector (정답 1, 아니면 0)

4. 학습 알고리즘

• mini batch → 기울기 산출 → 매개변수 갱신

1. 미니 배치
   : 훈련 데이터 중 일부를 무작위로 선택

2. 기울기 산출
   : 미니 배치에 대한 손실 함수 값 최소화
   : 경사 하강법, 경사 상승법 등

3. 매개변수 갱신
   : 가중치 매개변수를 기울기 방향으로 업데이트

5. 오차 역전파

• 기울기 산출의 단점 : 시간 소모
• 오차를 출력층 → 입력층 으로 전달
• 덧셈 노드, ReLu, Sigmoid, Affine 등

6. 활성함수

• 입력 신호의 총합 ▶ 출력신호
• 노드의 활성화 여부 결정

  • 퍼셉트론 : 1개 이상 입력층, 1개 출력층의 신경망 구조

  • 다층 퍼셉트론 : 퍼셉트론 + 은닉층 1개 이상, 계단 함수를 통해 0, 1 반환

  • 딥러닝 인공신경망 : 가중치 매개변수의 적절한 값 자동 학습

    Sigmoid
    : 이진분류
    : True (0.5 ~ 1), False (0 ~ 0.5)

    ReLu
    : Sigmoid의 기울기 소실 문제 해결
    : > 0 → 그대로 출력, ≤ 0 → 0

7. 과적합

• 학습 데이터에만 높은 성능을 보이는 경우
• 훈련 데이터 수가 적고, 매개변수가 많고, 표현력 높은 모델일 때 발생

해결법

1. Weight Decay : 가중치 감소
   : 가중치가 클수록 패널티 부과, 가중치 매개변수의 절대값 감소

• 패널티 종류

1. L1 규제 (Lasso)

   • L1-norm(벡터 요소의 모든 절대값 합)으로 비용 함수 조정

2. L2 규제 (Ridge)

   • L2-norm(벡터 간 유클리드 거리값)으로 비용 함수 조정
   • L1보다 활용도 높음

3. Dropout
   : 은닉층 뉴런을 임의로 삭제
   : 적은 뉴런으로 훈련, 전체 뉴런으로 테스트
   : 가중치가 높은 특정 뉴런에 대한 의존도 감소

4. Hyper Parameter 최적화
   : 교차검증과 함께 사용
   : Grid Search(가능한 모든 조합 시도)
   → Random Search(랜덤하게 하이퍼 파라미터 선택)
   → Bayesian Optimization(기존 결과 기반 다음 시도할 하이퍼 파라미터 추정)

8. 기울기 소실 : Vanishing Gradient

• 가중치 업데이트 이후, 역전파가 오차를 전파하는 와중 기울기가 소실되는 현상
• 입력 노드와 출력 노드 간 거리가 클수록 발생

해결법

1. ReLu
   : 양수값 기울기 일정 (1)

2. LSTM
   : 장기 기억 가능

3. GRU

4. 배치 정규화
   : 각 층에서의 데이터 분포 정규화

5. 최적화
   : Adam, AdaGrad 등

4-5. 딥러닝 모델 종류

1. CNN
   : 합성곱 신경망
   : Affine 계층 사용
   (인접 계층 모든 뉴런과의 완전 연결, ReLu or Sigmoid 사용)
   : 이미지 형상 유지, 이미지 특징 추출
   • Convolution Layer - Affine ReLu - Pooling Layer(생략 가능)

     CNN 과정

     1. Filter (kernel)
        : 벡터의 특징을 찾는 정사각형 행렬 파라미터
     2. stride
        : filter는 입력 데이터를 일정 간격(stride)로 순회하며 특징 추출해 feature map 구성
        : stride 크기 ∝ 1/출력데이터 크기
     3. Padding
        : Feature Map 크기 < 입력 데이터 → 출력 데이터 크기를 위해 주변을 0 or 1로 채움
        

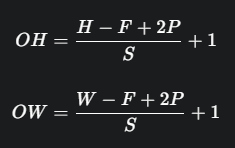
• Convolution Layer : 합성곱
  : 2차원 입력 데이터에 filter window 적용해 총합을 구하고, 합성곱 연산 출력
  • 입력 데이터의 채널 수 = filter의 채널 수
    (모든 채널의 filter 크기는 동일, bias는 항상 1개)

• Pooling Layer
  : Optional, 입력 데이터의 채널 수가 변화하지 않게 가로/세로 공간 감소
  ex) 4*4 행렬 → 2*2 행렬
  : Max Pooling (대상 영역의 최댓값으로 변환)
  : Average Pooling (대상 영역의 평균값으로 변환)
  : 과적합 감소 + 학습 시간 감소

2. RNN
   : Ordinary 시변적 특징 데이터 (필기, 음성인식 등)에 사용
   : 메모리를 통한 입력 시퀀스 처리
   : 순환 구조 은닉층을 가지며, 동일 가중치를 공유함
   : GSD(확률적 경사 하강법) 사용

   △ 단점
   : 관련 정보와 정보 사용 지점이 먼 경우, 역전파 시 기울기 소실 문제 발생

3. LSTM
   : RNN의 기울기 소실로 인한 데이터 소멸 문제 해결
   : 보통 신경망 대비 파라미터 수 x4
   : Long Term Memory
   : 입력/출력/망각 게이트 → 가중치 곱연산 → 활성화 함수 없이 컨트롤 게이트를 통해 조절

4. AutoEncoder
   : 입력으로 들어온 다차원 데이터 → 저차원 → 고차원 의 과정을 통해 특징 도출
   : 데이터 압축, 노이즈 제거 시 사용

   • encoder : 다차원 → 저차원
   • decoder : 저차원 → 고차원

5. GAN
   : 지도학습(판별자) + 비지도학습(생성자), 두 네트워크 간 MinMax Game

   • discriminator : 패턴 진위여부 판별

   • generator : 학습 데이터 패턴과 유사하게 생성

     DCGAN
     : 두 모델 중 하나로 역량이 치우쳐 성능 제약 문제가 발생하는 것을 해결

4-6. ANN 장단점

• 장점

1. 비선형적 예측 가능
2. 다양한 데이터 유형, 새로운 학습 환경에 적용 가능

• 단점

1. 데이터 양 ∝ 학습 시간
2. 모델에 대한 설명력↓

---

5. SVM

• 지도학습 중 하나
• 고차원 공간에서 초평면을 찾아 Classification, Regression 수행
• 두 데이터 집합을 바탕으로 새로운 데이터가 속할 카테고리 판단
  : 비확률적 이진 선형 분류

5-1. 주요 요소

1. vector : 점들 간 클래스
2. Decision Boundary : 클래스를 분류하는 선
3. hyperplane(초평면) : 서로 다른 분류에 속한 데이터 간 거리를 가장 크게 하는 선
4. Support vector : 두 클래스를 구분하는 경계
5. Margin : 서포트 벡터를 지나는 초평면 사이의 거리

5-2. 특징

• Margin최대화에 중점
  : 다른 분류기는 오류율 최소화에 중점

• 초평면의 마진 = 각 Support vector를 지나는 초평면 사이의 거리

• 가중치 벡터 : 초평면에 직교, offset 제공

• 선형 / 비선형 분류에 모두 사용

  비선형 분류에서의 SVM
  : 커널트릭(데이터 차원 증가)를 통해 하나의 초평면으로 분류

5-3. 장단점

• 장점

1. 분류, 회귀 예측 모두 활용 가능
2. 적은 데이터로도 학습 가능
   : 과적합, 과소적합↓
   : 데이터 수 ∝ 학습 시간

• 단점

1. 이진 분류 만 가능
2. 각 분류에 대한 SVM 별도 구축 필요

---

6. 연관성분석

• 유사 개체들을 그룹화하여 각 집단의 특성을 파악
  ▶ 사건의 연관 규칙 도출
• 비지도학습 중 하나, 탐색적 데이터 분석

6-1. 연관 규칙 순서

1. 데이터 간 규칙 생성
2. 데이터 특성에 부합되는 규칙 기준 설정
   • Support(지지도) : 데이터 전체에서 해당 사건이 나타나는 확률
   • Confidence(신뢰도) : 어떤 사건이 다른 사건에 대해 나타나는 확률
   • Lift(향상도) : 두 규칙(A, B)의 상관 관계
     : 1이면 독립, > 1 이면 양의 상관 관계
3. 규칙 생성
   : 빈발(frequent) 높은 것만 고려
   : Apriori 알고리즘 기반
   (최소 지지도 이상의 빈발항목집합에 대해서만 연관규칙 계산)

6-2. 장단점

• 장점

1. 분석결과 이해도 높음
2. 실적용에 용이함

• 단점

1. 품목수 ∝ 연관규칙 수
2. 계산과정이 많다.

---

7. 군집분석

• 비지도학습 중 하나
• 각 개체 간 유사성 분석을 통해 일반화 그룹 분류
• 이상치에 민감함, 신뢰성/타당성 검증X

7-1. 기본 가정

• 한 클러스터 내 개체 간 특성 동일
• 군집의 특성 = 군집 내 개체들의 평균

7-2. 군집분석 척도

유사성 계산 방법

1. 거리
   : 값이 작을수록 A, B가 유사함
   : 유클리드 거리, 맨해튼 거리

2. 유사성
   : 값이 클수록 A, B가 유사함
   : 코사인 값, 상관 계수

1. 유클리드 거리
   : 2차원에서 두 점을 잇는 가장 짧은 거리(피타고라스 정리)
   : 민코프스키 적용(m=2) 시, L2 거리

2. 맨해튼 거리
   : 가로지르지 않고 도착하는 최단거리
   : 민코프스키 적용(m=1) 시, L1 거리

3. 민코프스키 거리
   : m차원 민코프스키 공간에서의 거리
   : m = 1(맨해튼), m = 2(유클리드)

4. 마할라노비스 거리
   : 평균으로부터 특정 값의 거리
   : 변수 간 상관관계 고려

5. 자카드 거리
   : 두 집합 간 비유사성 측정

7-3. 군집분석 종류

군집분석은 병합과 분할로 구분
병합
: N개의 군집에서 시작해 1개까지 유사 군집 병합

분할
: 1개의 군집 → N개 될 때까지

1. 계층적 군집분석

• 상위-하위 구조로 군집 형성
• 군집 수 명시X
• 시각화 = 덴드로그램
• 최단, 최장, 평균, Ward 연결법, 계층적 병합 군집화

2. 비계층적 군집분석

• 사전 군집 수로 표본 구분

• 각 레코드를 정해진 군집에 할당

• 계산량이 적어 대용량 DB에서 유리

  K-means
  : 군집 내부 분산 최소화
  : 주어진 데이터를 k개의 클러스터 중 하나에 할당
  : 개별 유형 특징 파악에 용이
  : 대용량 데이터 처리, 분산 처리에 용이

  DBSCAN
  : 개체 간 밀도를 계산해 밀접 개체끼리 그룹핑
  : 이상치 제외 가능, 유형 간 밀도차이 뚜렷하지 않을 때 용이

  Gaussian Mixture Model : 확률 분포 기반 클러스터링
  : 데이터 확률 분포가 정규 분포라는 가정 아래,
  각 데이터가 정규 분포 상에서 어떤 분포에 속할 지 판단
  : 대용량 처리 시엔 적합하지 않음

7-4. 장단점

• 장점

1. 다양한 데이터 타입에 적용
2. 변수에 대한 정의가 없을 때 적용할 수 있음
   : 비지도 학습이니까

• 단점

1. 초기 군집 수, 관측치 간 거리 결정에 따라 결과 변동 가능
2. 주어진 사전 목표가 없다면 결과 해석이 어려움
   : 비지도 학습이니까