연속 부분수열 1
N개의 수로 이루어진 수열이 주어집니다.
이 수열에서 연속부분수열의 합이 특정숫자 M이 되는 경우가 몇 번 있는지 구하는 프로그램을 작성하세요.
만약 N=8, M=6이고 수열이 다음과 같다면
12131112
합이 6이 되는 연속부분수열은 {2, 1, 3}, {1, 3, 1, 1}, {3, 1, 1, 1}로 총 3가지입니다.
나의 풀이
function solution(m, arr){
let answer=lt=rt=sum=0;
while(lt<arr.length) {
if(sum===m) {
answer++;
sum -= arr[lt];
lt++;
} else if(sum<m) {
sum += arr[rt];
rt++;
} else {
sum -= arr[lt];
lt++;
}
}
return answer;
}
let a=[1, 2, 1, 3, 1, 1, 1, 2];
console.log(solution(6, a));정답 풀이
function solution(m, arr){
let answer=0, lt=0, sum=0;
for(let rt=0; rt<arr.length; rt++){
sum+=arr[rt];
if(sum===m) answer++;
while(sum>=m){
sum-=arr[lt++];
if(sum===m) answer++;
}
}
return answer;
}
let a=[1, 2, 1, 3, 1, 1, 1, 2];
console.log(solution(6, a));배운 점
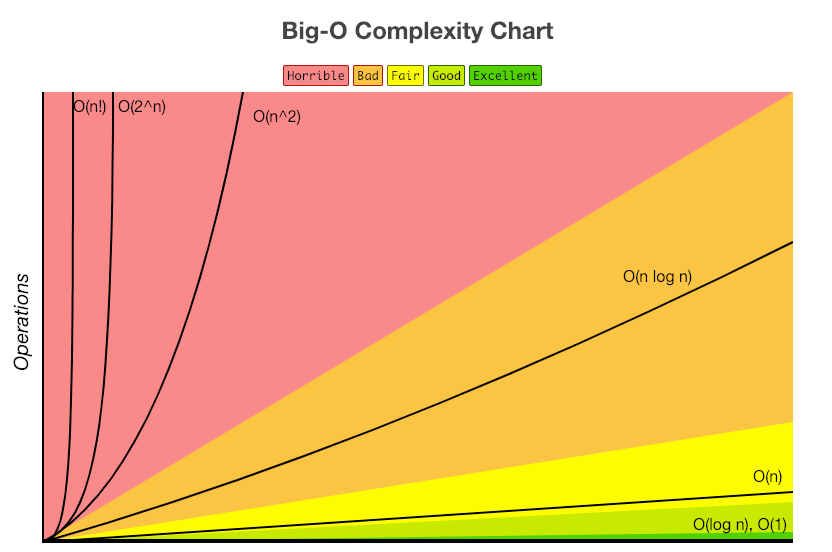
시간복잡도 개념에 대해 간략하게나마 알게 되었다. 기존에도 해당 개념에 대하여 알고는 있었지만 알고리즘 문제를 통해 해당 개념에 대해 생각해볼 계기는 부족했는데, 이번 문제를 처음 보았을 때, 이중 for문을 통하여 각각의 원소들을 더하는 방식으로 구하려 했으나, 강사님의 문제 설명을 듣고 현재 작성된 답의 방식으로 풀이를 했다. 그 결과,
O(n^2)의 시간 복잡도를 갖고있던 풀이가 O(n)의 시간 복잡도를 갖도록 바뀌었고, 더 간결한 풀이를 구할 수 있게 되었다.
연속 부분수열 2
N개의 수로 이루어진 수열이 주어집니다.
이 수열에서 연속부분수열의 합이 특정숫자 M이하가 되는 경우가 몇 번 있는지 구하는 프로그램을 작성하세요.
만약 N=5, M=5이고 수열이 다음과 같다면
13123
합이 5이하가 되는 연속부분수열은 {1}, {3}, {1}, {2}, {3}, {1, 3}, {3, 1}, {1, 2}, {2, 3}, {1, 3, 1}로 총 10가지입니다.
나의 풀이
function solution(m, arr){
let answer = 0;
for (let lt = 0; lt < arr.length; lt++) {
let i = 1, sum = 0;
sum += arr[lt];
if (sum < m) {
answer++;
while(lt+i<arr.length) {
sum += arr[i+lt];
if (sum > m) break;
answer++;
i++;
}
}
}
return answer;
}
let a=[1, 3, 1, 2, 3];
console.log(solution(5, a));정답 풀이
function solution(m, arr){
let answer=0, sum=0, lt=0;
for(let rt=0; rt<arr.length; rt++){
sum+=arr[rt];
while(sum>m){
sum-=arr[lt++];
}
answer+=(rt-lt+1);
}
return answer;
}
let a=[1, 3, 1, 2, 3];
console.log(solution(5, a));배운 점
같은 방식으로 투포인터 알고리즘을 활용하여 문제를 풀었다. 하지만 나의 풀이의 경우, 첫 합이 m을 넘는지를 if문으로 확인하고, 이후의 결과를 계속 더해주며 m을 초과할때까지 answer을 계속 더해주며 풀이를 진행하였으나, 정답 풀이의 경우 한번에 while문을 통하여 계속 값을 더해주고, m을 초과하기 전까지 몇개의 결과가 가능한지 여부를 구하여 한꺼번에 정답의 수를 늘려주는 방식을 사용했다. 해당 방식이 더 효율적인 방식이라고 생각되었다.
