level1 _ 소수 찾기

나의 답안

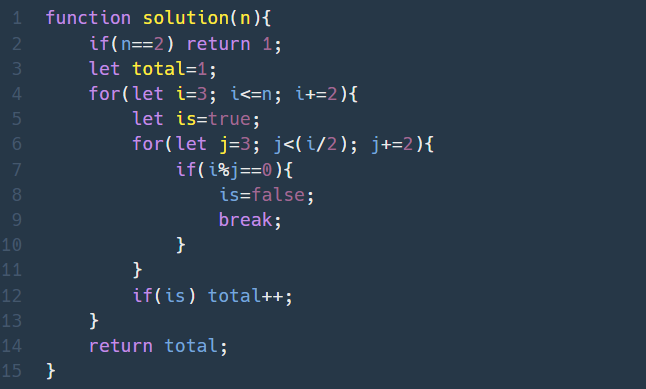
1. 2는 유일한 소수인 짝수이므로 먼저 예외처리
2. 3부터 n까지 각 수(i)의 소수 검사, 이 때 짝수는 제외
2-1. 해당 수(i)를 3부터 절반(i/2)에 해당하는 수까지 차례로 나누어보며(짝수는 미리 제외했으므로 나누는 수도 홀수만), 나누어떨어지는 수가 있으면 소수 자격 박탈!

-> 결과는 한두가지 케이스에서 시간 초과😭
아무래도 각 수를 모두 검사하는게 찝찝했다. 예를 들어 3의 배수, 5의 배수 등을 지워나가면 좋을 듯 한데 도저히 어떻게 구현할지 막막..

다른 답안

https://velog.io/@goblin820/%EC%BD%94%EB%94%A9%ED%85%8C%EC%8A%A4%ED%8A%B8-JavaScript-%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4-%EC%86%8C%EC%88%98-%EC%B0%BE%EA%B8%B0

"에라토스테네스의 체"
딱 상상했던 그 풀이다! 이미 정립된 이론이 있었구나.. 정확한 내용은 나무위키와 상단의 링크를 참고하여 이해해보았다.

미처 생각치 못했던 점은,

1. 주어진 수의 제곱근까지만 검사하면 된다.
(16이 주어졌을 경우 4까지만 검사해, 4 이하의 소수의 배수를 지우면 소수만 남게 된다.)

2. (소수의 배수로)남은 수를 지울 때, 찾은 소수의 제곱부터 지우면 된다.
(5의 배수를 지우고자 할 때, 10이나 15는 이미 2 또는 3의 배수로 지워진 상태이므로 25부터 30, 35... 순서대로 지우면 된다.)