이 글은 인프런 [하루코딩]님의 무료 강의 [Do it! 알고리즘 코딩테스트 with JAVA]를 따라가며,
직접 문제를 풀고 느낀 점, 새롭게 배운 개념 및 깨달음을 정리하는 글입니다.
문제마다 풀이 아이디어와 내가 고민했던 과정과 코드를 집어 넣었습니다.
모든 문제는 저작권 문제로 링크 형식으로 제공합니다.
목차
- 1. 백준 11659 구간합 구하기
- 2. 백준 2018 - 투포인터(수들의 합 5)
- 3. 백준 1940 - 투포인터(주몽)
- 4. 백준 12891 - 슬라이딩 윈도우(DNA 비밀번호)
- 5. 백준 11286 - 우선순위 큐(절댓값 힙)
1. 백준 11659 구간합 구하기
문제 링크
풀이
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int[] arr = new int[n + 1];
int[] prefixSum = new int[n + 1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
prefixSum[i] = prefixSum[i - 1] + arr[i]; // 누적합
}
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
System.out.println(prefixSum[end] - prefixSum[start - 1]);
}
}배운점 & 접근법
입력값과 배열 인덱스를 맞추기 위해 배열을 한 칸 더 크게 만들고, 0번 인덱스를 비워둔 채 1번부터 채워서 인덱스 혼동 없이 구현했다.
처음엔 단순 반복문으로 구간합을 직접 계산하다가 시간 초과가 발생해, 더 효율적인 방법을 고민함.
누적합(구간합) 배열을 사용하면, [start, end] 구간의 합을 prefixSum[end] - prefixSum[start - 1] 한 줄로 빠르게 구할 수 있다는 점화식적 사고로 접근했다.
이런 누적합 방식은 한 번의 전처리(O(N))만 하면, 이후 구간합 쿼리를 O(1)로 처리할 수 있어 효율적임을 알게 됐다.
2. 백준 2018 - 투포인터(수들의 합 5)
문제 링크
풀이
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int start = 1, end = 1, sum = 1, count = 0;
while (start <= N) {
if (sum < N) {
end++;
sum += end;
} else if (sum == N) {
count++;
sum -= start;
start++;
} else {
sum -= start;
start++;
}
}
System.out.println(count);
}배운점 & 접근법
- 투포인터 개념을 처음 명확하게 익힌 문제였다.
- 연속된 자연수의 합으로 N을 표현하는 경우의 수를 찾으려면,
구간의 시작과 끝을 가리키는 두 포인터(start, end)를 활용해 연속된 범위의 합을 구하는 "슬라이딩 윈도우" 방식이 필요하다. - start와 end 포인터를 적절히 움직이면서 현재 구간의 합이 N보다 작으면 end를 늘리고, 크거나 같으면 start를 이동시키는 식으로 문제를 해결했다.
- 단순히 반복문으로 모든 경우를 확인하면 시간 초과가 나기 때문에, 효율적인 투포인터 사용이 필수적이었다.
3. 백준 1940 - 투포인터(주몽)
문제 링크
풀이
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int m = Integer.parseInt(br.readLine());
String[] s = br.readLine().split(" ");
ArrayList<Integer> numList = new ArrayList<>();
for (String t : s) {
numList.add(Integer.parseInt(t));
}
Collections.sort(numList); // 오름차순 정렬
int count = 0;
int left = 0;
int right = n - 1;
while (left < right) {
int sum = numList.get(left) + numList.get(right);
if (sum == m) {
count++;
left++;
right--;
} else if (sum < m) {
left++;
} else {
right--;
}
}
System.out.println(count);
}배운점 & 접근법
- 정렬 후, 투포인터를 활용해 문제를 해결해야 한다는 점이 포인트였다.
- 이 문제는 임의의 두 수의 합이 특정 값이 되는 쌍의 개수를 찾는 문제이기 때문에,
배열을 정렬한 후, 양 끝(left, right)에서 접근하는 투포인터 방식이 적합하다. - 처음에는 2018번에서 사용한 "연속된 구간" 투포인터 방식으로 접근했다가,
정답이 제대로 나오지 않아 자료구조/정렬 방식을 다시 점검했다. - 이 과정에서 투포인터의 "구간"과 "쌍" 패턴은 적용 대상이 다르다는 걸 직접 체감했다.
- Map/Set을 사용해 풀 수도 있지만, 투포인터 연습을 위해서 정렬 + 투포인터가 더 직관적이고 효율적이었다.
📝 "투포인터"의 유형별 시작 위치와 적용 방식
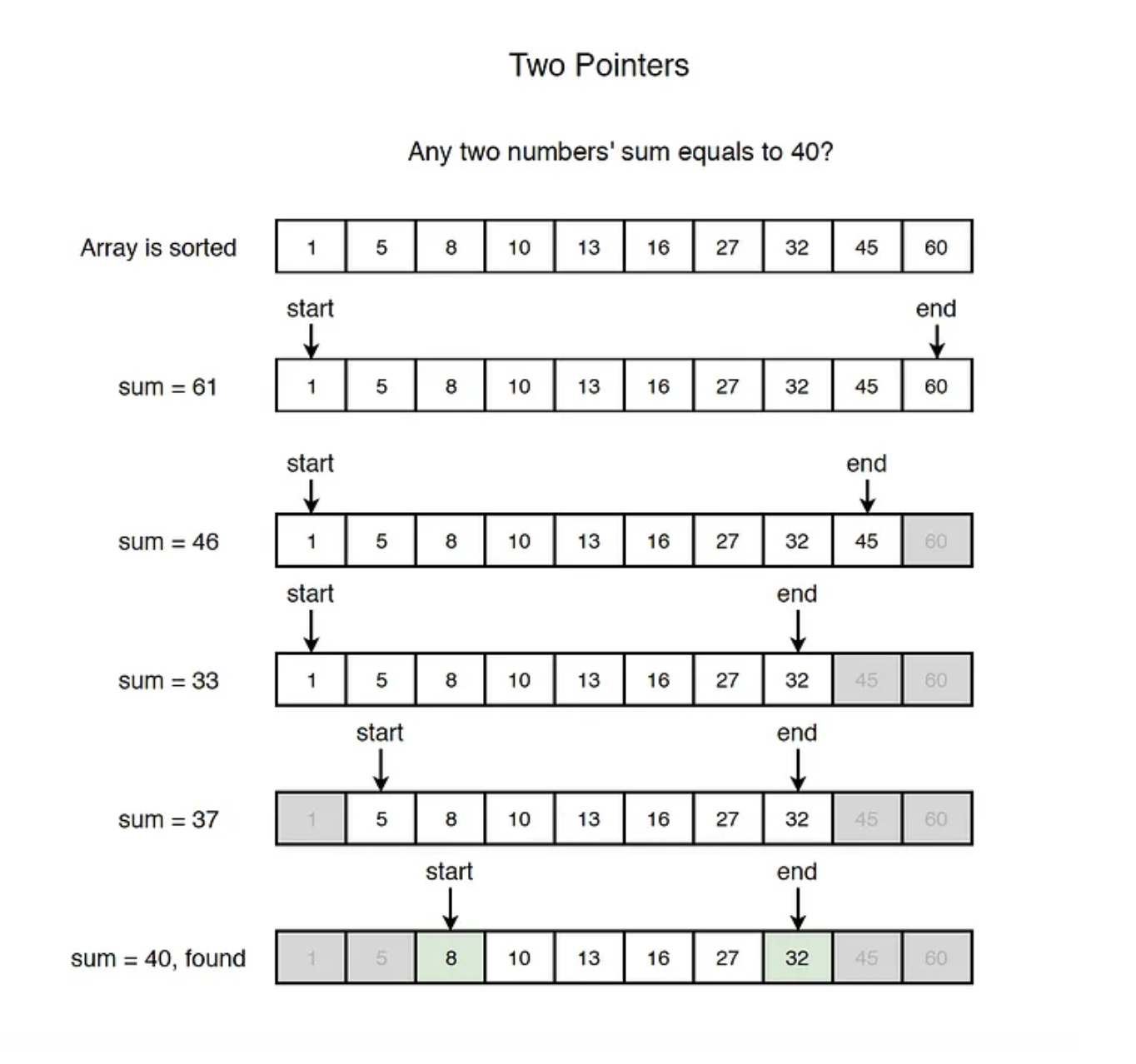
1. 구간(연속된 범위)형: "연속 부분합/구간" 문제
- 적용 대상
- 연속된 원소들의 합, 곱, 길이 등 ‘구간’ 자체의 특징을 묻는 문제
- 예시: [백준 2018번 수들의 합 5], [백준 12891 DNA 비밀번호], [부분합(연속된 최소/최대 구간)]
- 포인터 위치
- start와 end, 두 개의 포인터를 같은 쪽(처음)에서 출발
- 한 쪽(보통 end) 또는 양쪽을 이동시키며 "구간"을 확장/축소함
- 구간의 합(혹은 다른 조건)이 "목표"에 미달하면 end++, 초과하면 start++
(조건 만족 시 count 증가 등)
- 패턴 예시
while (start <= N) { if (sum < 목표) { end++; sum += arr[end]; } ... }- 즉, start와 end가 처음부터 출발, "연속된 범위"를 확장/축소
2. 쌍/조합형(임의 두 원소 조합)
- 적용 대상
- 배열/리스트 내 임의의 두 수(쌍)의 합/곱/차 등을 만족하는 쌍의 개수, 조합
- 예시: [백준 1940번 주몽], [투포인터로 푸는 2sum 류], [두 배열 합이 특정값]
- 포인터 위치
- 정렬 후, left=0(첫 원소), right=N-1(마지막 원소)에서 “양끝”에서 접근
- 두 수의 합이 목표값보다 작으면 left++, 크면 right--
- 쌍의 조건을 만족하면 count 증가 후 둘 다 이동(혹은 한쪽만 이동)
- 패턴 예시
while (left < right) { int sum = arr[left] + arr[right]; ... }- 즉, 정렬된 배열의 "양끝에서" 출발해서 서로 가까워짐
✔️ 정리
- 연속된 범위/구간의 조건 → 투포인터(동일 방향, "연속 범위" 탐색)
- 슬라이딩 윈도우(Sliding Window)로도 불림. 투포인터의 대표적 응용!
- 배열에서 쌍/조합 조건 → 투포인터(양끝에서, "조합/합" 탐색)
문제에서 “연속된 구간/부분합”이냐, “임의의 쌍/조합”이냐를 먼저 구분하면
투포인터의 시작 위치와 이동 방식이 자연스럽게 결정된다!
💡 참고: 슬라이딩 윈도우란?
- 슬라이딩 윈도우는 위에서 말한 "연속 범위"형 투포인터의 한 방식으로,
일정 크기의 구간(윈도우)을 한 칸씩 밀면서 빠르게 조건을 체크하는 패턴을 뜻합니다. - 투포인터로 시작점/끝점을 관리해 구간 정보를 효율적으로 유지합니다.
4. 백준 12891 - 슬라이딩 윈도우(DNA 비밀번호)
문제 링크
풀이
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int length = Integer.parseInt(st.nextToken()); // DNA 문자열 길이
int answer_length = Integer.parseInt(st.nextToken()); // 비밀번호(부분문자열) 길이
String s = br.readLine();
char[] charArray = s.toCharArray();
st = new StringTokenizer(br.readLine());
// 최소 조건 map
HashMap<Character, Integer> minMap = new HashMap<>();
minMap.put('A',Integer.parseInt(st.nextToken()));
minMap.put('C',Integer.parseInt(st.nextToken()));
minMap.put('G',Integer.parseInt(st.nextToken()));
minMap.put('T',Integer.parseInt(st.nextToken()));
// 윈도우 내 현재 카운트 map
HashMap<Character, Integer> windowMap = new HashMap<>();
windowMap.put('A', 0);
windowMap.put('C', 0);
windowMap.put('G', 0);
windowMap.put('T', 0);
int result = 0;
// 초기 윈도우 세팅
for (int i = 0; i < answer_length; i++) {
char c = charArray[i];
windowMap.put(c, windowMap.get(c) + 1);
}
if (isSatisfied(minMap, windowMap)) result++;
// 슬라이딩 윈도우
for (int i = answer_length; i < length; i++) {
// 윈도우 오른쪽 문자 추가
char in = charArray[i];
windowMap.put(in, windowMap.get(in) + 1);
// 윈도우 왼쪽 문자 제거
char out = charArray[i - answer_length];
windowMap.put(out, windowMap.get(out) - 1);
if (isSatisfied(minMap, windowMap)) result++;
}
System.out.println(result);
}
// 최소 조건을 만족하는지 체크하는 함수
private static boolean isSatisfied(HashMap<Character, Integer> minMap, HashMap<Character, Integer> windowMap) {
for (char c : minMap.keySet()) {
if (windowMap.get(c) < minMap.get(c)) return false;
}
return true;
}배운점 & 접근법
- 처음에는 각 구간마다 등장하는 문자의 개수를 확인하기 위해, HashMap과 이중 for문을 활용해 모든 부분 문자열마다 조건을 검사하는 방식으로 문제를 풀었다.
- 하지만 이중 for문은 매번 윈도우(부분 문자열)를 새로 검사해야 하므로 비효율적(시간복잡도 O(NL))이라는 한계를 느꼈다.
- 효율적인 방법을 고민하다가, '슬라이딩 윈도우(Sliding Window)'라는 알고리즘 패턴을 접했다.
- 슬라이딩 윈도우를 적용하니, 한 칸씩 윈도우를 이동할 때마다 새로 등장/사라지는 문자만 업데이트해서 훨씬 빠르게 풀 수 있었다.
- 이번 문제를 통해 “구간 합/카운팅”이 필요한 경우, 단순 완전탐색보다 슬라이딩 윈도우 기법을 우선적으로 고민해볼 필요가 있다는 점을 배웠다.
💡 슬라이딩 윈도우란?
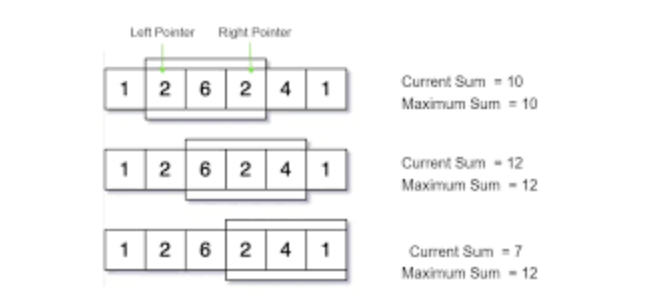
- 슬라이딩 윈도우는 연속된 구간(부분 배열/부분 문자열 등)에 대한 계산을 효율적으로 처리하는 알고리즘 기법입니다.
- "시작점과 끝점" 두 개의 포인터를 사용해서 고정된 크기의 윈도우(구간)를 왼쪽에서 오른쪽으로 이동시키며,
윈도우가 이동할 때 바뀌는 부분만 빠르게 갱신합니다.(맨앞 , 맨뒤) - 이 방식을 활용하면, 매번 전체 구간을 다시 계산하는 것보다 훨씬 빠르게 문제를 해결할 수 있습니다.
"부분합/카운팅"과 같이 연속된 범위에서 뭔가를 구하는 문제가 나오면 사용
문제를 풀고 개념을 정리하다보니, 문득 드는 생각이 있었다.
'투포인터와 슬라이딩 윈도우.. 너무 비슷한데?' 그래서 비교 해봤다.
🤔 투포인터 vs 슬라이딩 윈도우, 뭐가 달라?
🤔 투포인터 vs 슬라이딩 윈도우, 뭐가 달라?
| 투포인터 | 슬라이딩 윈도우 | |
|---|---|---|
| 개념 | 인덱스 두 개로 구간/조합 탐색 | 고정 크기 구간(윈도우) 한 칸씩 이동 |
| 패턴 | 두 포인터 독립/양방향 이동 | 윈도우 범위 고정, 한쪽만 이동 |
| 적용 예시 | 연속합/쌍/조합/부분합(2018,1940,2sum) | 구간합/빈도(12891, 부분문자열 카운트 등) |
| 특징 | 구간 확장·축소/양끝 조합/자유 이동 | 구간 크기 고정/추가·제거만 갱신 |
| 관계 | 투포인터가 “상위 개념”, 슬라이딩 윈도우는 하위 | 투포인터의 특수형 |
- 모든 슬라이딩 윈도우는 투포인터다!
(단, 모든 투포인터가 슬라이딩 윈도우는 아님) - 슬라이딩 윈도우는 “구간(윈도우) 크기 고정”에서 추가/제거만 관리하며 효율을 높이는 “투포인터 활용법”이다.
5. 백준 11286 - 우선순위 큐(절댓값 힙)
문제 링크
풀이
public static void main(String[] args) throws IOException {
StringBuilder sb = new StringBuilder();
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int length = Integer.parseInt(br.readLine());
int[] arr = new int[length];
for (int i = 0; i < length; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
PriorityQueue<Integer> pq = new PriorityQueue<>(
(a,b) -> {
if (Math.abs(a) == Math.abs(b)) {
return a - b;
} else {
return Math.abs(a) - Math.abs(b);
}
}
);
for (int x : arr) {
if (x == 0) {
if (pq.isEmpty()) {
sb.append(0);
sb.append("\n");
}else{
Integer poll = pq.poll();
sb.append(poll);
sb.append("\n");}
} else {
pq.add(x);
}
}
System.out.println(sb.toString());
}
배운점 & 접근법
- 처음에는 일반적인 큐로 접근했으나, 코드가 점점 비효율적인 방법으로 길어졌다.
- 큐에 다른 종류의 자료구조를 찾아보다가, 우선순위 큐라는 자료구조를 접했고, 활용 해보기로 했다.
- 추상클래스나 람다형식으로 사용하는게 편하겠다고 느꼈고, 그 부분에 대해서 좀 더 자세하게 공부하면서 문제에 적용 해봤다.
여기서 추가적으로, 우선순위 큐의 정렬 기준을 직접 커스터마이징 하다보니
Comparable과 Comparator의 차이점도 자연스럽게 알게 되었다.
두 인터페이스의 핵심 차이는 다음과 같다:
- Comparable : "자기 자신(this)과 매개변수 객체를 비교"
- Comparator : "두 매개변수 객체를 비교"
✅ Comparable
- 클래스 내부에서 정렬 기준을 직접 구현하고,
한 클래스에 한 가지 정렬 기준만 제공할 수 있다.
public class Student implements Comparable<Student> {
int score;
public Student(int score) { this.score = score; }
@Override
public int compareTo(Student o) {
return this.score - o.score; // 오름차순
}
}
PriorityQueue<Student> pq = new PriorityQueue<>();
)PriorityQueue는 기본적으로 comparator가 null이기 때문에,
내부적으로 compareTo() 메서드 기준으로 정렬하게 된다.
✅ Comparator
- 클래스 외부에서 별도의 정렬 기준을 만들 수 있고,
여러 기준을 동적으로 지정할 수 있다.
V2. 별도 구현 클래스 사용
import java.util.Comparator;
public class ScoreDescComparator implements Comparator<Student> {
@Override
public int compare(Student a, Student b) {
return b.score - a.score; // 내림차순
}
}
PriorityQueue<Student> pq = new PriorityQueue<>(new ScoreDescComparator());
)V3. 익명 클래스 사용
PriorityQueue<Student> pq = new PriorityQueue<>(
new Comparator<Student>() {
@Override
public int compare(Student a, Student b) {
return b.score - a.score; // 내림차순
}
}
);
)V4. 람다식 사용
PriorityQueue<Student> pq = new PriorityQueue<>(
(a, b) -> b.score - a.score // 내림차순
);
)✅ 결론
- Comparable은 클래스 내부에서 고정된 정렬 기준을 제공
- Comparator는 외부에서 다양한 기준으로 유연하게 정렬 가능
이번 문제를 풀면서 Comparable과 Comparator의 동작 방식을 실제로 체득할 수 있었고,
특히 람다식으로 간단하게 정렬 기준을 작성할 수 있어 실전에도 적극 활용할 수 있을 것 같다.
마무리 및 느낀 점
- 자료구조를 활용한 알고리즘 문제는 무조건 실습해봐야 감이 생긴다
“왜 이 방식이 시간/공간 면에서 효율적인가?”,
“내가 직접 손으로 움직이면 어떻게 되지?”
를 생각하며 반복하니 확실히 이해가 깊어진다. - 각 문제별로 "내가 처음 막혔던 포인트", "실전에서 어떤 상황에 적용할지"를 메모해두면 나중에 큰 자산이 될 것 같다.

