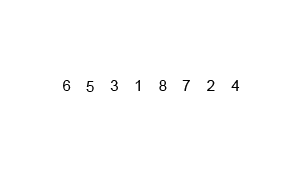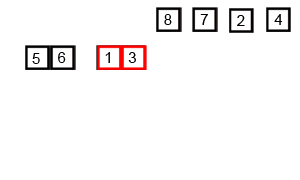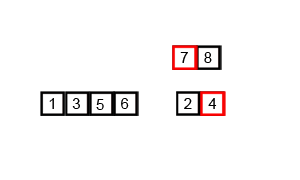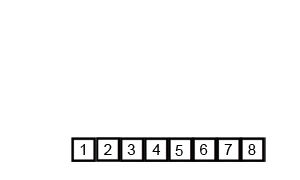정렬 알고리즘(Java Code)

러브굿·2023년 8월 27일

정렬 알고리즘

정렬 알고리즘이란 원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘이다.

정렬 알고리즘을 알아보기전에 자주 사용되는 swap함수를 먼저 구현하고 진행하자.

swap() 설명

public static void swap(int[] arr, int idx1, int idx2) {
	int tmp = arr[idx1];
    arr[idx1] = arr[idx2];
    arr[idx2] = tmp;
}

배열의 두 인덱스의 원소를 교환하는 메소드이다.
정렬의 특성상 자주 사용되며 다음에 나올 예시들에서도 사용될 것이다.

버블 정렬(Bubble Sort)

Code

public static void sortByBubbleSort(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                swap(arr, j, j + 1);
            }
        }
    }
}

정렬 과정에서 거품이 수면으로 올라오는 모습과 흡사하여 지어진 이름이다.
비교와 교환이 모두 일어날 수 있기 때문에 코드는 단순하지만 성능은 좋지 않다.

시간 복잡도
worst: O(n^2)
average: O(n^2)
best: O(n^2)

선택 정렬(Selection Sort)

Code

public static void sortBySelectionSort(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        int minIdx = i;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[minIdx]) {
                minIdx = j;
            }
        }
        swap(arr, i, minIdx);
    }
}

맨 앞 인덱스부터 차례대로 들어갈 원소를 선택하여 정렬하는 알고리즘이다.

교환 횟수는 O(n)으로 적지만, 비교는 모두 진행된다.
즉, 버블 정렬보다는 성능이 좋다.

시간 복잡도
worst: O(n^2)
average: O(n^2)
best: O(n^2)

삽입 정렬(Insertion Sort)

Code

public static void sortByInsertionSort(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        int tmp = arr[i];
        int j = i - 1;
        while (j >= 0 && tmp < arr[j]) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = tmp;
    }
}

인덱스 1의 원소부터 앞 방향으로 들어갈 위치를 찾아 교환하는 정렬 알고리즘이다.

정렬이 되어 있는 배열의 경우 O(n)의 속도로 정렬되어 있을 수록 성능이 좋다.

시간 복잡도
worst: O(n^2)
average: O(n^2)
best: O(n)

합병(병합) 정렬(Merge Sort)

Code

public static void sortByMergeSort(int[] arr) {
    int[] tmpArr = new int[arr.length];
    mergeSort(arr, tmpArr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int[] tmpArr, int left, int right) {
    if (left < right) {
        int m = left + (right - left) / 2;
        mergeSort(arr, tmpArr, left, m);
        mergeSort(arr, tmpArr, m + 1, right);
        merge(arr, tmpArr, left, m, right);
    }
}
public static void merge(int[] arr, int[] tmpArr, int left, int mid, int right) {
    for (int i = left; i <= right; i++) {
        tmpArr[i] = arr[i];
    }
    int part1 = left;
    int part2 = mid + 1;
    int index = left;
    while (part1 <= mid && part2 <= right) {
        if (tmpArr[part1] <= tmpArr[part2]) {
            arr[index] = tmpArr[part1];
            part1++;
        } else {
            arr[index] = tmpArr[part2];
            part2++;
        }
        index++;
    }
    for (int i = 0; i <= mid - part1; i++) {
        arr[index + i] = tmpArr[part1 + i];
    }
}

재귀를 수행하는 부분인 mergeSort()와 재귀를 마치고 합병하는 부분인 merge()로 구성된다.

mergeSort()는 반으로 나누면서 재귀호출하며 다 나눠졌으면 점점 올라오면서 merge()한다.

merge()는 두 부분 배열의 인덱스를 점차적으로 비교하면서 정렬한다.
while문이 끝나고 배열에 좌측 부분배열의 남은 것만 저장하는 이유는 다음과 같다.
1. 우측 부분배열이 다 들어가고 좌측 부분배열만 남은 경우에는 좌측 부분 배열만 넣으면 됨.
2. 좌측 부분배열이 다 들어가고 우측 부분배열만 남은 경우에는 이미 배열은 다 정렬된 것.
2번이 이해가 잘 안될 수도 있는데, 정렬을 단계별로 그려보면 이해가 될 것이다.

분할 정복 알고리즘 중 하나이다.
배열의 길이가 1이 될 때까지 2개의 부분 배열로 분할한다.
분할이 완료됐으면 다시 2개의 부분 배열을 합병하고 정렬한다.
모든 부분 배열이 합병될 때 까지 반복한다.

시간 복잡도가 O(nlog n)으로 빠르지만, 아래 코드를 보면 tmpArr을 사용해야 돼서 제자리 정렬보다 O(n)만큼 추가적인 메모리가 사용되는 단점이 있다.
보통은 재귀함수로 구현하므로 이 것또한 메모리를 많이 사용하게 된다.

시간 복잡도
worst: O(nlog n)
average: O(nlog n)
best: O(nlog n)
공간 복잡도
O(n)만큼의 추가 메모리 tmpArr 사용

힙 정렬(Heap Sort)

Code

public static void sortByHeapSort(int[] arr) {
    for (int i = arr.length / 2 - 1; i < arr.length; i++) {
        heapify(arr, i, arr.length - 1);
    }
    for (int i = arr.length - 1; i >= 0; i--) {
        swap(arr, 0, i);
        heapify(arr, 0, i - 1);
    }
}
public static void heapify(int[] arr, int parentIdx, int lastIdx) {
    int leftChildIdx;
    int rightChildIdx;
    int largestIdx;
    while (parentIdx * 2 + 1 <= lastIdx) {
        leftChildIdx = (parentIdx * 2) + 1;
        rightChildIdx = (parentIdx * 2) + 2;
        largestIdx = parentIdx;
        if (arr[leftChildIdx] > arr[largestIdx]) {
            largestIdx = leftChildIdx;
        }
        if (rightChildIdx <= lastIdx && arr[rightChildIdx] > arr[largestIdx]) {
            largestIdx = rightChildIdx;
        }
        if (largestIdx != parentIdx) {
            swap(arr, parentIdx, largestIdx);
            parentIdx = largestIdx;
        } else {
            break;
        }
    }
}

오름차 순 정렬일 때 최대힙을 사용하는 정렬이다. (내림차는 최소힙)
최대힙을 배열로 구현하면 0번째 인덱스가 가장 큰 수라는 점을 사용한다.

시간 복잡도가 O(nlog n)으로 합병정렬, 퀵정렬과 동일하지만 실상 성능은 더 낮게 나온다.
매번 루트에서 최대 값을 뺄 때마다 heapify()를 사용하여 다시 최대힙으로 만들어야 해서 그렇다.

시간 복잡도
worst: O(nlog n)
average: O(nlog n)
best: O(nlog n)

퀵 정렬(Quick Sort)

Code

public static void sortByQuickSort(int[] arr) {
    quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int left, int right) {
    int part = partition(arr, left, right);
    if (left < part - 1) {
        quickSort(arr, left, part - 1);
    }
    if (part < right) {
        quickSort(arr, part, right);
    }
}
public static int partition(int[] arr, int left, int right) {
    int pivot = arr[(left + right) / 2];
    while (left <= right) {
        while (arr[left] < pivot) {
            left++;
        }
        while (arr[right] > pivot) {
            right--;
        }
        if (left <= right) {
            swap(arr, left, right);
            left++;
            right--;
        }
    }
    return left;
}

피벗(pivot)을 사용한 정렬 알고리즘이며 합병 정렬과 같은 분할 정복 알고리즘이다.
합병 정렬은 일정한 부분 리스트로 분할하지만 퀵 정렬은 피벗이 들어갈 위치에 따라 불균형하다.

합병 정렬과 속도가 비슷하고 힙 정렬보다 빠르지만, 최악의 경우 O(n^2)만큼 걸린다는 점, 보통 재귀로 구현하기 때문에 메모리를 더 사용할 수 있다는 단점이 있다.
최악의 경우는 피봇을 최솟값이나 최댓값 으로 선택하여 부분 배열이 한쪽으로 계속 몰리는 경우이다.

시간 복잡도
worst: O(n^2)
average: O(nlog n)
best: O(nlog n)

참조 > https://ko.wikipedia.org/wiki/
https://velog.io/@pppp0722/%EC%A0%95%EB%A0%AC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-7%EA%B0%9C-%EC%A0%95%EB%A6%AC-Java#%ED%9E%99-%EC%A0%95%EB%A0%ACheap-sort