모듈러 연산 with BOJ 2981(검문)

YU_DAVID·2023년 7월 4일
모듈러연산백준알고리즘유클리드호제법최대공약수칸아카데미파이썬
1

Algorithm: 이론과 적용

목록 보기
1/3

1. 들어가며

백준 2981 검문 문제를 풀기 시작했다.
시간초과가 날 것을 알면서도, 일단 문제를 명확히 이해할 겸 naive한 방법으로 풀었다. 결과는 역시나 시간초과.

시간을 줄일 방법을 찾기 위해 구글에 "나머지가 같은 수 찾기"와 같은 키워드로 검색하며 여러 글들을 훑어본 끝에 모듈러 연산을 공부하면 해답을 찾을 수 있을 것 같았다.

칸 아카데미에 마침 모듈러 연산 파트가 있어서 그 부분을 공부했다.

2. 모듈러 연산(modular arithmetic) 공부

✅ 참고: 칸 아카데미 모듈러 연산

  • 모듈러 연산(modular arithmetic)이란?
    • 나머지를 구하는 연산이다.
    • A mod B = R
      • “A 모듈러(modulo) B는 R이다.”
      • mod: 모듈러 연산자(modulo operator)
      • B: 모듈(modulus)

  • 합동(congruence)
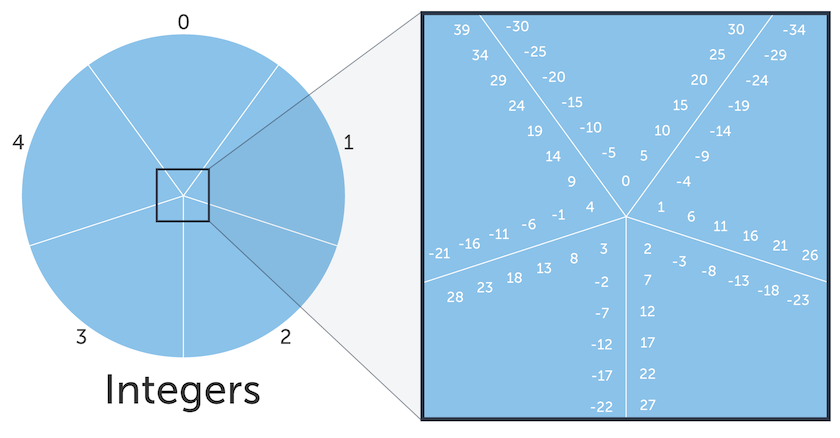    이미지 출처: https://cdn.kastatic.org/ka-perseus-images/2b71fee76257ba0bdc1e4b2b64249abe7e30c2d5.png
    • A≡B (mod C)
      • “A와 B는 모듈 C에 대해 합동이다.”
    • 위 그림에서, 같은 구역에 있는 숫자들은 구역을 구분하는 모듈에 대해 서로 합동이다.
      • ex. 26≡11 (mod 5)
    • 모듈 C에 대해 합동인 두 수의 차는 C의 배수다.
      • 26-11 = 15 → 15 = 5 * 3
    • 다음 식들은 서로 동치관계이다.
      • A≡B (mod C)
      • A mod C=B mod C
      • C ∣ (A−B) (The | symbol means divides, or is a factor of)
      • A=B+K⋅C (where K is some integer)

  • 여러 성질들
    • 덧셈/뺄셈 성질(the addition/subtraction property of modular arithmetic)
      • (A + B) mod C = (A mod C + B mod C) mod C
      • (A - B) mod C = (A mod C - B mod C) mod C
    • 곱셈 성질(the multiplication property of modular arithmetic)
      • (A * B) mod C = (A mod C * B mod C) mod C
    • 지수 성질(the exponentiation property of modular arithmetic)

  • 역수(Modular inverse)
    • (A * B) mod C = 1
    • A 모듈러 C의 모듈러 역수는 위 식을 만족하는 B값이다.
    • C와 서로소인 수만 모듈러 역수를 갖는다.

  • 유클리드 호제법(The Euclidean Algorithm)
    • 최대공약수(GCD: Greatest Common Divisor)를 빠르게 찾는 기법
    • 과정
      1. A=0이면 GCD(0,B)=B이므로 GCD(A,B)=B.
      2. B=0이면 GCD(A,0)=A이므로 GCD(A,B)=A.
      3. 1, 2에 해당하지 않을 경우: A를 A = B⋅Q + R의 형식으로 쓴다.
      4. GCD(A,B) = GCD(B,R)이므로 유클리드 호제법을 이용하여 GCD(B,R)을 찾는다.
      5. 1-4 반복

3. 문제 풀이: BOJ 2981(검문)

✅ 문제: BOJ 2981

다시 문제로 돌아왔다.
사실 모듈러 연산을 공부하고 나서 바로 해법이 떠오르지는 않았다. 그래서 본 문제를 푼 다른 사람들의 코드와 해설을 참고하여 문제를 풀었다. 나의 코드는 아래와 같다.

import sys
from math import sqrt
from collections import deque

sys.stdin = open('2981_input.txt')

# 유클리드 호제법을 통한 최대공약수 구하기
# n1 >= n2
def gcd(n1, n2):
    if n2 == 0:
        return n1
    else:
        return gcd(n2, n1 % n2)

# 약수 구하기
def cds(n):
    cds = deque()
    sqrt_value = sqrt(n)
    for i in range(2, int(sqrt_value) + 1):
        if n % i == 0:
            cds.append(i)
    
    start = len(cds) - 1
    
    # 제곱근이 약수일 경우 제곱근이 한 번 더 추가되지 않도록 인덱스 이동
    if sqrt_value in cds:
        start -= 1
    
    # 쌍을 이루는 약수 추가
    for j in range(start, -1, -1):
        cds.append(n // cds[j])
    
    # n 추가
    cds.append(n)
    return cds

N = int(sys.stdin.readline())

nums = deque()
for _ in range(N):
    nums.append(int(sys.stdin.readline()))
nums = sorted(nums)

# 두 숫자의 차이를 저장할 deque
diff = deque()
for i in range(1, N):
    diff.append(nums[i] - nums[i - 1])

# 차이들의 최대공약수 구하기
now_gcd = 0
for i in range(N - 1):
    if now_gcd >= diff[i]:
        now_gcd = gcd(now_gcd, diff[i])
    else:
        now_gcd = gcd(diff[i], now_gcd)

# 약수 구하기
cds = cds(now_gcd)
cds = list(map(str, cds))
cds = ' '.join(cds)
print(cds)

이 문제를 해결하기 위해 2가지를 고려해야 한다.

1) 숫자 간 차이의 최대공약수 활용

입력 숫자가 A, B, C, D일 때, 각 숫자는 문제에서 찾아야 하는 값인 M을 활용해 표현할 수 있다.
그리고 숫자 간 차를 통해 M이 숫자 간 차들의 공약수라는 것을 알 수 있다.

A = Ma + R
B = Mb + R
C = Mc + R
D = Md + R

B - A = M(b - a)
C - B = M(c - b)
D - C = M(d - c)

모든 공약수를 효율적으로 구하기 위해 먼저 유클리드 호제법으로 최대공약수를 구한 후, 최대공약수의 약수를 구하는 방식으로 코드를 작성했다.

2) 연산 최소화

입력으로 들어오는 숫자의 범위가 1이상 10억 이하이기 때문에 반복문에 신경을 쓰지 않으면 시간초과가 발생한다.
가장 신경써야 하는 반복문은 최대공약수의 약수를 구할 때이다. 최대공약수를 2부터 최대공약수 사이 값으로 모두 나눠가며 약수를 구하면 안 된다.

나는 2부터 최대공약수의 제곱근 까지만 순회를 하며 약수를 구했고, 해당 약수와 짝을 이루는 약수(예를 들어 최대공약수가 10일 경우, 2와 5는 짝을 이룸)를 후에 추가하는 방식으로 연산량을 줄였다.

profile
YU_DAVID
.
다음 포스트

다시 한 번 모듈러 연산 with BOJ 10830(행렬 제곱)

0개의 댓글