다익스트라 알고리즘(Dijkstra Algorithm)

정의

도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘

그래프의 최단 경로를 찾는 문제

• 하나의 정점에서 다른 하나의 정점까지의 최단 경로를 구하는 문제(single source and single destination shortest path problem)

• 하나의 정점에서 다른 모든 정점까지의 최단 경로를 구하는 문제(single source shortest path problem) => 다익스트라

• 하나의 목적지로가는 모든 최단 경로를 구하는 문제(single destination shortest path problem)

• 모든 최단 경로를 구하는 문제(All pairs shortest path problem)

제한

• 간선들은 모두 양의 가중치를 가진다.

기본 로직(Array)

• 시간 복잡도 : $O(V^{2})$ (V는 정점의 개수)

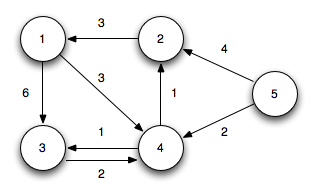
시작 정점을 5로 두고 시작한다.
5번의 가중치를 0으로 두고 아직 나머지의 가중치는 모르니 무한대로 둔다.

5	4	3	2	1
0	$\infty$	$\infty$	$\infty$	$\infty$

5번 노드에서 경로가 짧은 정점을 고른다.
5-2 경로의 경우 $\infty$와 4 중 짧은 것을 고른다.
즉 dist[2] = Math.min(dist[2], dist[5] + adj[5][2])이 된다. 이는 dist[5] + adj[5][2], 4이다.
5-4 경로도 마찬가지로 2가 된다.

5	4	3	2	1
0	$\infty$	$\infty$	$\infty$	$\infty$
0	2	$\infty$	4	$\infty$

그리고 2의 가중치를 가진 4번 노드는 가장 짧으므로 해당 노드에서 인접한 노드를 찾는다.
인접 노드는 2와 3이다.
위의 공식과 같이 갱신해준다.
3번 노드의 경우 $\infty$와 dist[4] + adj[4][3] 즉 2+1로 3이다.
2번 노드의 경우 4와 dist[4] + adj[4][2] 즉 2+1 로 3이다.

5	4	3	2	1
0	$\infty$	$\infty$	$\infty$	$\infty$
0	2	$\infty$	4	$\infty$
0	2	3	3	$\infty$

3과 2 둘다 가중치가 같다. 3에서 인접한 노드는 4
dist[4] 와 dist[3]+adj[3][4] 중 작은 것은 기존 값이다.
갱신하지 않는다.

5	4	3	2	1
0	$\infty$	$\infty$	$\infty$	$\infty$
0	2	$\infty$	4	$\infty$
0	2	3	3	$\infty$

2에서 인접한 노드는 1 하나이다.
$\infty$와 dist[2] + adj[2][1] 즉 3+3=6이다.
1에서 인접한 노드는 4와 3
계산해도 갱신되지 않는다.

5	4	3	2	1
0	$\infty$	$\infty$	$\infty$	$\infty$
0	2	$\infty$	4	$\infty$
0	2	3	3	$\infty$
0	2	3	3	6

결과는 다음과 같다.

BFS와 유사한 느낌으로 탐색한다는 것을 알 수 있다.

우선순위 큐(Heap)을 이용한 다익스트라

• 시간복잡도 : $O((V+E)logV)$ (V는 정점의 개수, E는 한 정점의 주변 노드)

모든 정점들을 우선순위 큐에 넣는다.
우선순위는 가중치이다.
기본적으로 우선순위 큐에 넣을 때 5를 제외한 나머지 정점들은 가중치를 무한대로 둔다.

• Priority Queue

Index	가중치	이전 정점
5	0	-1
4	$\infty$	NULL
3	$\infty$	NULL
2	$\infty$	NULL
1	$\infty$	NULL

• dist 배열

5	4	3	2	1
0	$\infty$	$\infty$	$\infty$	$\infty$

큐에서 가장 위의 값을 꺼낸다.
기존 배열의 값과 비교하여, 같거나 크면 연산한다.
0으로 둘다 같으므로, 5와 인접한 정점을 찾고, dist 배열보다 작은 가중치라면 Queue에 넣고 배열도 갱신해준다.

Index	가중치	이전 정점
4	2	5
2	4	5
4	$\infty$	NULL
3	$\infty$	NULL
2	$\infty$	NULL
1	$\infty$	NULL

• dist 배열

5	4	3	2	1
0	2	$\infty$	4	$\infty$

큐에서 값을 꺼내어 기존 배열과 비교하는 위의 연산을 수행한다.
4를 꺼내었을때의 결과는 인접한 2와 3을 연산하는 것이다.

Index	가중치	이전 정점
2	3	4
3	3	4
2	4	5
4	$\infty$	NULL
3	$\infty$	NULL
2	$\infty$	NULL
1	$\infty$	NULL

• dist 배열

5	4	3	2	1
0	2	3	3	$\infty$

큐에서 값을 꺼내어 기존 배열과 비교하는 위의 연산을 수행한다.
2를 꺼내었을때의 결과는 인접한 1을 연산하는 것이다.
우선순위가 가중치이기 때문에 6인 1번 노드는 아래로 내려간다.

Index	가중치	이전 정점
3	3	4
2	4	5
1	6	2
4	$\infty$	NULL
3	$\infty$	NULL
2	$\infty$	NULL
1	$\infty$	NULL

• dist 배열

5	4	3	2	1
0	2	3	3	6

큐에서 값을 꺼내어 기존 배열과 비교하는 위의 연산을 수행한다.
3를 꺼내었을때의 결과는 인접한 4를 연산하는 것이다.
4를 연산했을 때는 3번의 가중치 3과 3->4의 거리 2를 더한 5인데,
이는 dist[4]보다 크므로 queue에 넣지 않고 배열의 갱신도 하지 않는다.

Index	가중치	이전 정점
2	4	5
1	6	2
4	$\infty$	NULL
3	$\infty$	NULL
2	$\infty$	NULL
1	$\infty$	NULL

• dist 배열

5	4	3	2	1
0	2	3	3	6

남은 Queue의 가중치들은 배열의 값들보다 크다.
Queue가 빌 때까지 확인해주며 제거하면 현재의 dist배열을 볼 수 있다.

예제 문제 - 백준 1753번

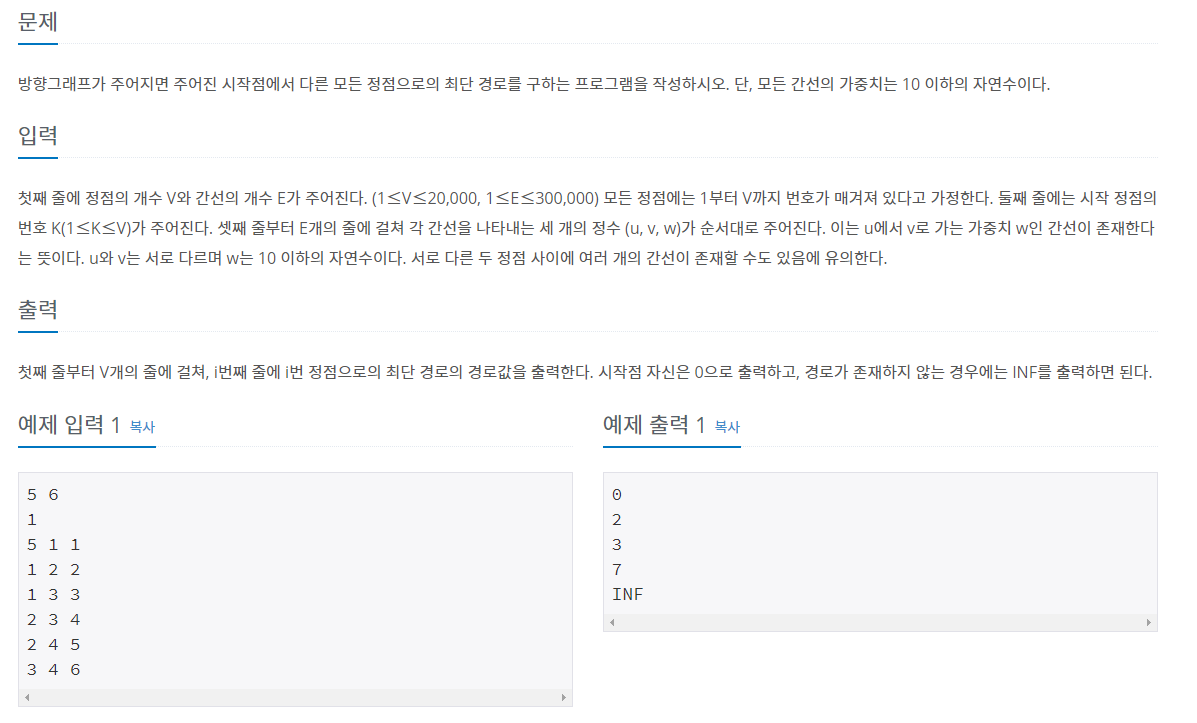
코드 - JAVA

import java.io.*;
import java.util.*;


class Main {
    static ArrayList<Edge>[] adj;
    static boolean[] check;
    static int[] dist;
    public static void main(String[] args) throws Exception {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer stringTokenizer = new StringTokenizer(br.readLine());
        int V = Integer.parseInt(stringTokenizer.nextToken());
        int E = Integer.parseInt(stringTokenizer.nextToken());
        int start = Integer.parseInt(br.readLine());
        adj = new ArrayList[V+1];
        for (int i = 1; i <= V; i++)
            adj[i] = new ArrayList<>();
        for(int i=0; i<E; i++){
            stringTokenizer = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(stringTokenizer.nextToken());
            int v = Integer.parseInt(stringTokenizer.nextToken());
            int w = Integer.parseInt(stringTokenizer.nextToken());
            adj[u].add(new Edge(v,w));
        }
        check = new boolean[V+1];
        dist = new int[V+1];

        dijkstra(start);

        StringBuilder stringBuilder = new StringBuilder();
        for(int i=1; i<=V; i++){
            if(dist[i]!=Integer.MAX_VALUE)
                stringBuilder.append(dist[i] + "\n");
            else
                stringBuilder.append("INF\n");
        }
        System.out.print(stringBuilder.toString());
    }

    public static void dijkstra(int start){
        PriorityQueue<Edge> priorityQueue = new PriorityQueue<>();
        Arrays.fill(dist,Integer.MAX_VALUE);
        priorityQueue.add(new Edge(start,0));
        dist[start] = 0;
        while (!priorityQueue.isEmpty()) {
            Edge edge = priorityQueue.poll();
            int destination = edge.destination;
            if(check[destination])
                continue;
            else
                check[edge.destination] = true;
            for (Edge next : adj[destination]) {
                if (dist[next.destination] >= dist[destination] + next.weight) {
                    dist[next.destination] = dist[destination] + next.weight;
                    priorityQueue.add(new Edge(next.destination,dist[next.destination]));
                }
            }
        }
    }
}

class Edge implements Comparable<Edge> {
    int destination;
    int weight;

    public Edge(int destination, int weight) {
        this.destination = destination;
        this.weight = weight;
    }

    @Override
    public int compareTo(Edge o) {
        // TODO Auto-generated method stub
        return Integer.compare(this.weight, o.weight);
    }
}

설명에서는 언급하지 않았지만, visit배열같은 방문을 체크하는 배열을 만들어 체크해주어야한다.