백준 13549번 - 숨바꼭질3

solved.ac 백준 골드문제 포스팅

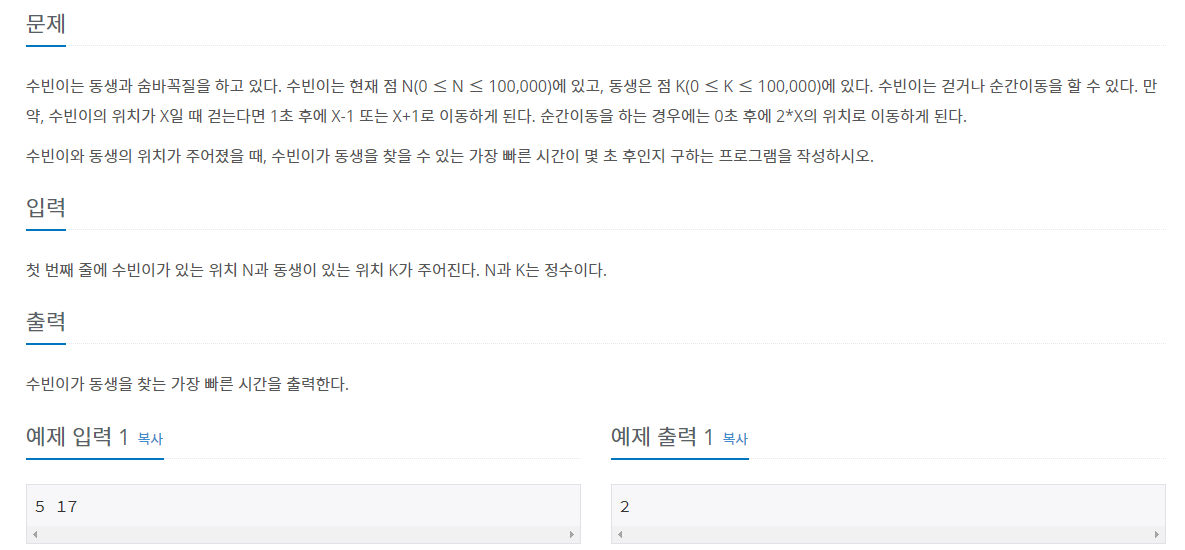
문제

BFS

너비 우선 탐색, 그래프 탐색 시 형제 노드를 우선하여 탐색한다.
추후 다른 포스팅에서 DFS와 함께 정리 예정

접근법

출발지를 루트 노드라고 생각하고, 자식 노드를 2배, -1, +1이라 생각하고 너비 우선 탐색을 한다.
그렇게 탐색하던 중 처음으로 같은 값이 나오면, 그때까지 수행했던 시간 값이 가장 빠른 시간 값이 된다.

이 접근법에서는 2배, -1, +1 순서로 너비 우선 탐색을 하는 것이 중요하다.

ex) 4 에서 12로

*2 -1 +1 순으로 집어넣는경우. 3->6 으로 진행 되는 동작이 5->6 으로 진행 되는 동작보다 먼저 일어나므로 4->3->6->12 1초.

*2 +1 -1 순으로 집어넣는경우. 5->6으로 진행되는 동작이 3->6보다 먼저 진행되어 3->6 으로 queue에 들어가지지 않음. 4->5->6->12 2초.

주의

그냥 너비 우선 탐색을 수행하면 이전에 계산했던 값 위에 한번 더 계산을 하게 되는데, 이러면 가장 빠른 시간을 구할 수 없다.

코드 - JAVA

import java.io.*;
import java.util.*;


class Main {
    static int N = 0;
    static int K;
    public static void main(String args[]) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer str = new StringTokenizer(br.readLine());
        N = Integer.parseInt(str.nextToken());
        K = Integer.parseInt(str.nextToken());
        if(N >= K)
            System.out.println(N-K);
        else
            System.out.println(bfs(N, K));
    }

    static int bfs(int N, int K) {
        Queue<Integer> q = new LinkedList();
        int[] arr = new int[100001];//체크 및 저장
        Arrays.fill(arr, -1);

        q.add(N);
        arr[N] = 0;

        while(!q.isEmpty()) {
            int now = q.poll();
            if(now == K)
                return arr[now];
            int tmp = now * 2;
            while(tmp <= 100000 && arr[tmp] == -1) {
                arr[tmp] = arr[now];
                q.add(tmp);
                tmp *= 2;
            }

            for(int i=0; i<2; i++) {
                int next;
                if(i == 0)
                    next = now - 1;
                else
                    next = now + 1;
                if(0 <= next && next <= 100000) {
                    if(arr[next] == -1) {
                        q.add(next);
                        arr[next] = arr[now] + 1;
                    }
                }
            }
        }
        return 0;
    }
}