백준 2263번 - 트리의 순회

solved.ac 백준 골드문제 포스팅

문제

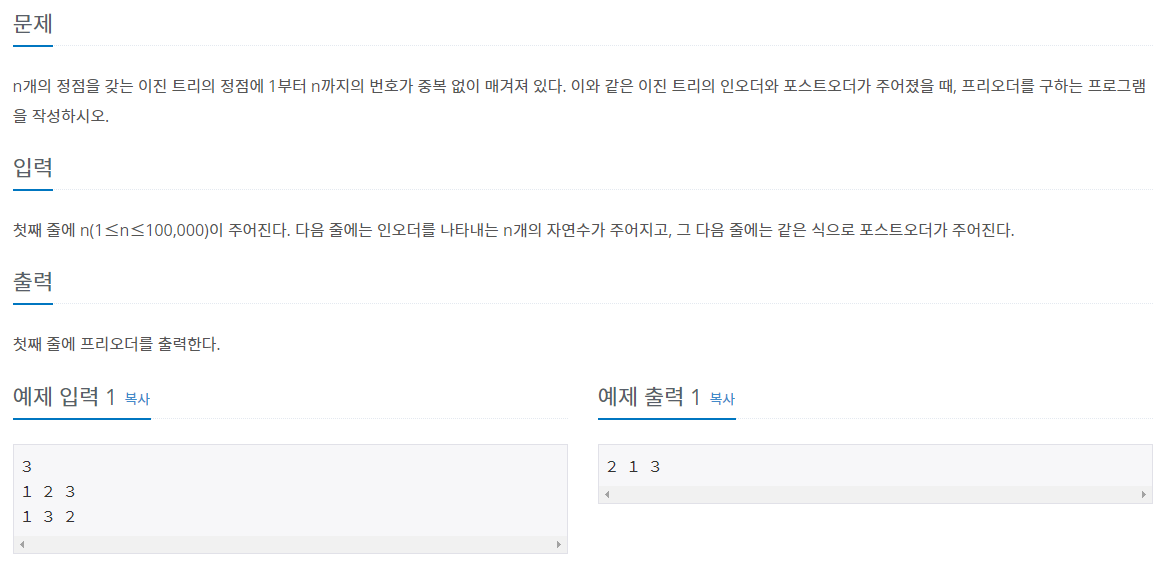
트리 순회

트리 순회(Tree traversal)는 트리 구조에서 각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정

• PreOrder(전위 순회)
  전위 순회(preorder)는 다음과 같은 방법으로 진행한다.

  1. 노드를 방문한다.
  2. 왼쪽 서브 트리를 전위 순회한다.
  3. 오른쪽 서브 트리를 전위 순회한다.

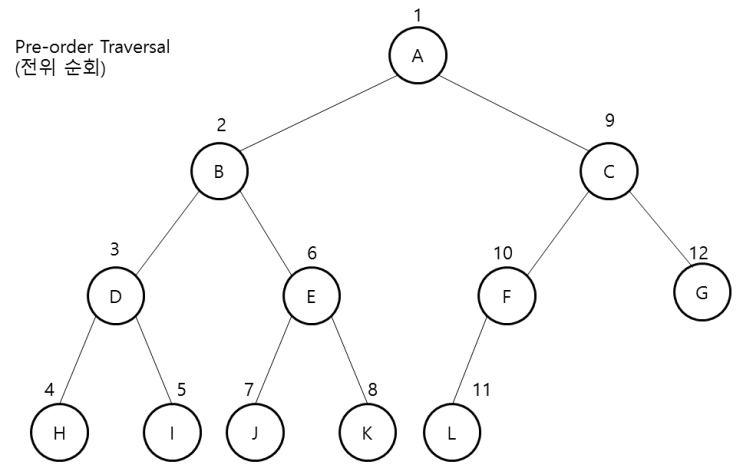
• InOrder(중위 순회)
  중위 순회(Inorder)은 다음의 순서로 진행된다.

1.왼쪽 서브 트리를 중위 순회한다.
2. 노드를 방문한다.
3. 오른쪽 서브 트리를 중위 순회한다.

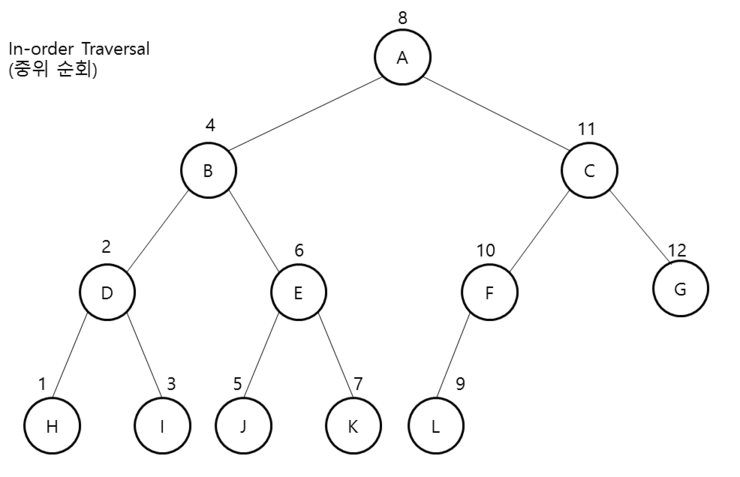
• PostOrder(후위 순회)
  후위 순회(PostOrder)는 다음과 같은 방법으로 진행한다.

1.왼쪽 서브 트리를 후위 순회한다.
2. 오른쪽 서브 트리를 후위 순회한다.
3. 노드를 방문한다.

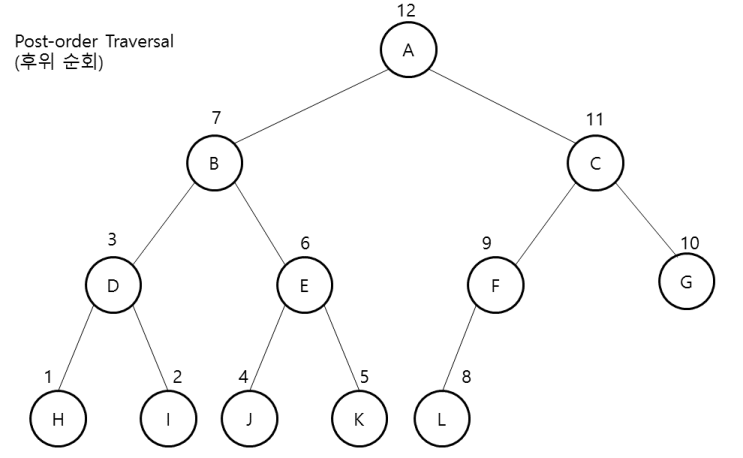
접근법

다음 문제는 분할-정복 방식과 유사하다.
위의 예시 그래프들을 예로 들어 설명해보면,

중위 순회 : HDIBJEKALFCG
후위 순회 : HIDJKEBLFGCA

후위 순회에서의 마지막 노드는 Root 노드이다.
중위 순회에서 루트 노드를 기준으로 왼쪽과 오른쪽을 나누면, 그 작은 덩어리가 Root 노드의 왼쪽 오른쪽이 된다.
그렇게 나누어가면서 생기는 Root 노드를 저장하면, 그 순서가 PreOrder가 된다.

주의사항

Root 노드를 재귀의 형태로 분할 정복 해나갈 때, PreOrder는 Left노드를 우선 탐색하기 때문에 재귀 함수의 선언시 왼쪽 먼저 해주어야 PreOrder가 찍힌다.

코드 - JAVA

import java.io.*;
import java.util.*;


class Main {
    static int N = 0;
    static int inOrder[];
    static int postOrder[];
    static int arr[];
    static StringBuilder result = new StringBuilder();
    public static void main(String args[]) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        StringTokenizer str = new StringTokenizer(br.readLine());
        inOrder = new int[N+1];
        postOrder = new int[N+1];
        arr = new int[N+1];
        for(int i=1; i<=N; i++){
            inOrder[i] = Integer.parseInt(str.nextToken());
        }
        str = new StringTokenizer(br.readLine());
        for(int i=1; i<=N; i++){
            postOrder[i] = Integer.parseInt(str.nextToken());
        }
        for(int i=1; i<=N; i++){
            arr[inOrder[i]] = i;
        }
        circulation(1,N,1,N);
        System.out.print(result.toString().trim());
    }

    public static void circulation(int postStart, int postEnd, int inStart, int inEnd){
        if(postStart>postEnd||inStart>inEnd)
            return;
        result.append(postOrder[postEnd]+" ");
        int tmp = arr[postOrder[postEnd]];
        int left = tmp-inStart;
        circulation(postStart,postStart+left-1, inStart,tmp-1);
        circulation(postStart+left,postEnd-1,tmp+1,inEnd);
    }
}