
알고리즘 분류: 그래프 이론
문제
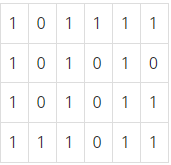
N×M크기의 배열로 표현되는 미로가 있다.
[출처] https://www.acmicpc.net/problem/2178
미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.
위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.
입력
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
출력
첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.
예제 입출력
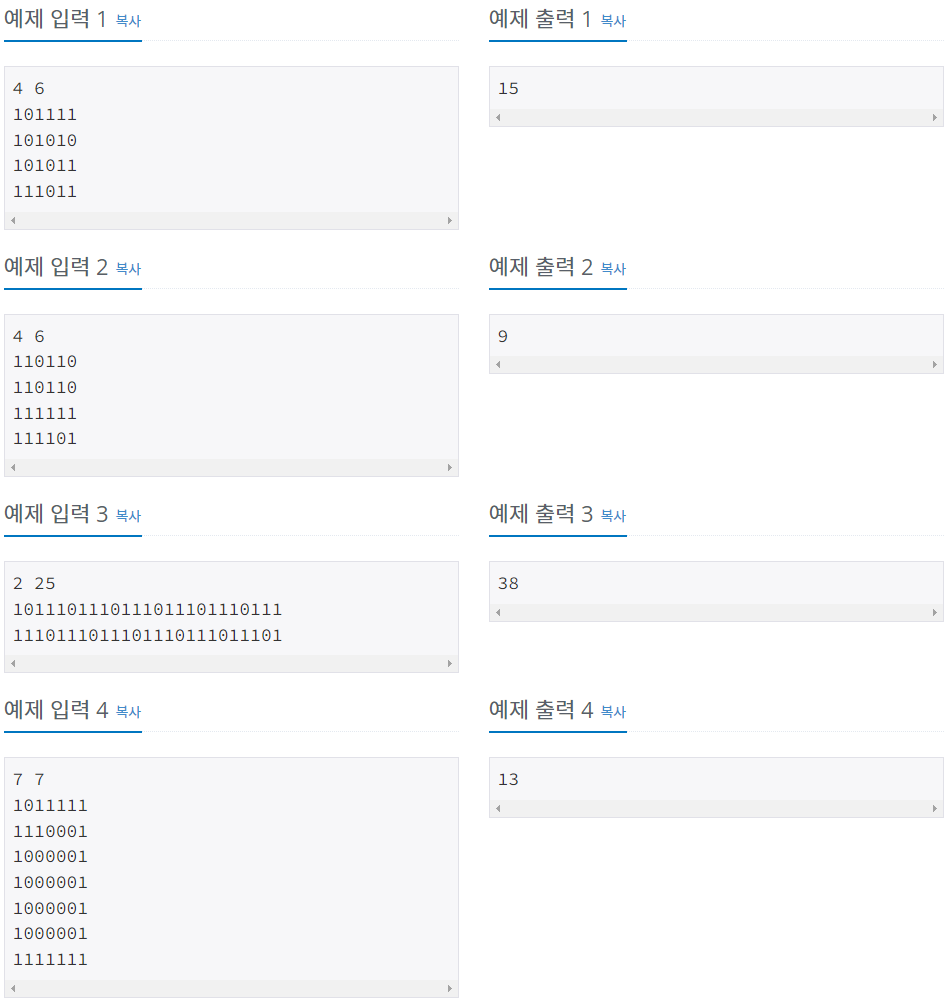
접근
이 문제를 읽어보면 이전에 올린 나이트의 이동(7562번)과 동일한 문제라고 생각이 들었을 것이라고 생각한다.
다른점은 나이트의 이동(7562번)의 경우, 나이트가 이동하는 것이므로 8가지의 대각선 이동으로 인해 인접노드가 8가지였고, 이 문제는 상하좌우만 이동이 가능하기 때문에 인접노드가 최대4개로 나이트의 이동(7562번)보다도 쉬운 문제이다.
접근 아이디어는 다음과 같다.
1. 그래프 판단
우선 주어진 내용과 그림을 보고 이것이 격자형 그래프라는 것을 판단하는 것이 중요하다고 생각한다.
위에서 이야기한대로 격자의 각 칸을 노드로 보면, 이동할수 있는 상하좌우, 그중에서도 1인 부분만 이동이 가능하므로 이를 만족하는 칸들이 인접한 노드가 되어 그래프 모양으로 생각할 수 있다.
그리고 갈수 있는 길을 이용해서 목적지에 도달하는 최소값을 구하는 것이므로 탐색문제라고 볼 수 있다.
2. 탐색 알고리즘 선정
그래프로 보았고, 그래프를 탐색해나가는 문제라는 것을 알았으면 탐색하는 알고리즘을 선정해야된다.
여기서는 bfs방법을 이용해서 미로를 탐색해 나갈것이다.
3. 그래프 만들기
탐색알고리즘도 정했으면, 탐색할 그래프를 만들어주어야 한다.
입력에 미로의 row가 문자열로 들어오기 때문에 2차원 배열로 만들기 위해서 map함수를 이용한다.
4. 탐색
그래프가 만들어졌고, 탐색알고리즘이 정해졌으며, 시작노드가 주어졌으면 탐색을 하면 된다.
상하좌우로 이동할수 있기 때문에 현재노드에 더해서 다음노드를 구할dx,dy를 정의해준다.
시작노드를 큐에 넣고 방문처리를 한다.
방문확인은 1이상 이면 방문하지 않아서 방문해야되는 곳(탐색하지 않은 위치)이고 0이면 방문한것 또는 할수 없는 곳이다.
다음 노드로 갈때마다 이미 지나친 노드들은 전부 0으로 바꿔버려서 탐색처리를 해준다.
큐에서 꺼낸 값이 목적지 값이면 그대로 저장된 값을 꺼내주면 된다.
5. 코드
코드에 주석을 달아놔서 위의 설명과 함께 읽으면 이해가 될 것이라고 생각한다.
import sys
from collections import deque
'''입력'''
#n:세로, m: 가로
n,m = map(int,sys.stdin.readline().split())
#그래프 생성
graph = []
for _ in range(n):
graph.append(list(map(int,sys.stdin.readline().strip())))
#bfs 정의 - 그래프 탐색이 다 끝나면 목적지 값을 리턴
def bfs(start_node:list,graph:list) -> int:
#상하좌우 이동정의
dx = [0,0,-1,1]
dy = [-1,1,0,0]
#방문체크는 graph에 함(0이 아닌 수를 비교하는 식으로)
need_visited= deque(list())
need_visited.append(start_node)
while need_visited:
current_x,current_y = need_visited.popleft()
if current_x == n-1 and current_y == m-1:
break
for i in range(4):
next_x = current_x + dx[i]
next_y = current_y + dy[i]
#아래 로직에서 1이면 탐색안한것으로 생각하도록 했는데, 시작노드의 경우에 첫번째라서 값이 계속 1이므로 , 시작노드면 패스하도록 함.
# if next_x == 0 and next_y == 0:
# continue
#좌표평면을 벗어나지 않아야되고 갈수 있는 위치(0이 아니여야됨)여야됨
if next_x >=0 and next_x < n and next_y >=0 and next_y < m and graph[next_x][next_y] >= 1:
#현재노드+1값과 해당 노드의 값과 비교해서 현재노드+1값이 더 작으면 업데이트, 또는 1이면 아직 업데이트가 안됨.
# if graph[current_x][current_y] + 1 < graph[next_x][next_y] or graph[next_x][next_y] == 1:
if graph[next_x][next_y] == 1:
graph[next_x][next_y] = graph[current_x][current_y] + 1
need_visited.append([next_x,next_y])
#방문한곳을 0으로 바꿔버리면 다른 노드에서 인접노드가 이 노드라고 해도 탐색하지 않음
#해당노드는 인접노드 일 수도 있고, 여러번거친 노드일수도 있는데 인접노드 추가후에 값을 0으로 바꿔버리면 다음에 탐색을 안함.
#즉 맨처음 갔을때가 최소값이기 때문에 탐색할 필요가 없음
#이렇게 하면 시작노드가 1이라서 위에서 조건문을 하나 더 추가해서 continue하도록 한 로직도 필요 없어짐
graph[current_x][current_y] = 0
return graph[n-1][m-1]
start_node = [0,0]
print(bfs(start_node,graph))결과
