보간(Interpolation)이란?
보간은 주어진 데이터 포인트 사이의 값을 추정하는 수학적 기법이다.
측정된 데이터의 일부 값이 누락되어있거나 조밀하지 않은 경우 보간을 통해 그 중간 값을 예측할 수 있다.
ex)
x = 1, 2, 3
y = 2, ?, 6
이 때 x = 1과 x = 3의 값을 이용해 x = 2를 추정할 수 있으며 이러한 과정을 보간이라고 한다.
보간의 종류에는 선형 보간(Linear Interpolation)과 비선형 보간(Nonlinear Interpolation)이 있다.
- 선형 보간(Linear Interpolation)
선형 보간은 빠르고 구현이 간단하다는 장점이 있지만, 데이터가 급격히 변하거나 곡선 형태를 가지는 경우에는 부정확할 수 있다.
public class LinearInterpolation {
public static double interpolate(double x1, double y1, double x2, double y2, double x) {
return y1 + (x - x1) * (y2 - y1) / (x2 - x1);
}
public static void main(String[] args) {
double x = 2.0;
double result = interpolate(1.0, 2.0, 3.0, 6.0, x);
System.out.println("x=" + x + "일 때 보간된 y 값: " + result);
}
}
- 비선형 보간(Nonlinear Interpolation)
대표적인 기법 중 하나로 스플라인(Spline) 이 있는데 여러 개의 다항식을 연결해서 곡선을 만드는 방식으로, 데이터 변화가 부드러운 그래프로 표현된다.
수학적으로는 복잡하지만 데이터의 정밀한 보간이 필요한 경우에 유리하다.
import org.apache.commons.math3.analysis.interpolation.SplineInterpolator;
import org.apache.commons.math3.analysis.polynomials.PolynomialSplineFunction;
public class SplineInterpolationExample {
public static void main(String[] args) {
double[] x = {1.0, 2.0, 3.0};
double[] y = {2.0, 4.0, 6.0};
SplineInterpolator interpolator = new SplineInterpolator();
PolynomialSplineFunction spline = interpolator.interpolate(x, y);
double result = spline.value(2.5);
System.out.println("x=2.5일 때 보간된 y 값: " + result);
}
}그래프로 시각화 방법
1. Java 2D (Swing + Graphics2D)
자바 표준 GUI 라이브러리인 Swing과 Graphics2D 클래스를 활용해 직접 그래프를 그리고 보간 결과를 시각화한다.
ex:
-. 선형 보간, 다항 보간 곡선 등을 점과 선으로 그리기
-. 실시간 보간 결과 시각화
장점:
-. 별도 라이브러리 없이 가능
-. 커스터마이징 자유로움
단점:
-. 개발이 번거롭고 반복 작업 많음
2. JFreeChart
다양한 차트를 쉽게 만들 수 있는 강력한 차트/시각화 라이브러리
ex:
-. 원본 데이터와 보간된 곡선을 같이 선 그래프로 표시
-. 다중 시리즈 (original vs interpolated) 비교
장점:
-. 빠르게 차트 만들기 가능
-. PNG, SVG 저장 가능
단점:
-. 복잡한 UI 연동에는 부적합
3. JavaFX
Swing보다 강력한 UI 툴킷으로, 애니메이션 및 인터랙션에 강함
ex:
-. 보간 곡선의 애니메이션 시각화
-. 마우스 이벤트로 값 추적
장점:
-. CSS 스타일링, 그래픽 효과, 애니메이션 등 UI 표현에 유리
단점:
-. 러닝 커브 존재, 설치 환경 따라 설정 필요
4. Processing
Java 기반의 시각화 특화 프레임워크
ex:
-. 데이터 기반 곡선 시각화
-. 보간된 포인트 연결 애니메이션
장점:
-. 코드가 직관적이고 빠르게 결과 확인 가능
단점:
-. 일반 Java 애플리케이션과 연동 시 별도 처리 필요
그래프로 시각화 해보기 - JFreeChart
- build.gradle에 application 플러그인을 추가해준다.
plugins {
id 'java'
id 'application'
}- 의존성 추가
dependencies {
// JFreeChart 라이브러리
implementation 'org.jfree:jfreechart:1.5.4'
// 보간 계산하기 위한 라이브러리
implementation 'org.apache.commons:commons-math3:3.6.1'
}- java 소스코드 작성
import org.apache.commons.math3.analysis.interpolation.SplineInterpolator;
import org.apache.commons.math3.analysis.polynomials.PolynomialSplineFunction;
import org.jfree.chart.ChartFactory;
import org.jfree.chart.ChartPanel;
import org.jfree.chart.JFreeChart;
import org.jfree.chart.plot.PlotOrientation;
import org.jfree.data.xy.XYSeries;
import org.jfree.data.xy.XYSeriesCollection;
import javax.swing.*;
import java.util.stream.IntStream;
public class Main {
public static void main(String[] args) {
double[] xData = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
double[] yData = {2, 4, 7, 11, 9, 8, 12, 14, 17, 25};
int N = xData.length;
double[] t = IntStream.range(0, N).mapToDouble(i -> (double) i / (N - 1)).toArray();
SplineInterpolator interpolator = new SplineInterpolator();
PolynomialSplineFunction fx = interpolator.interpolate(t, xData);
PolynomialSplineFunction fy = interpolator.interpolate(t, yData);
int numPoints = 100;
double[] tNew = IntStream.range(0, numPoints)
.mapToDouble(i -> (double) i / (numPoints - 1))
.toArray();
XYSeries originalSeries = new XYSeries("Original");
XYSeries interpolatedSeries = new XYSeries("Interpolated");
for (int i = 0; i < N; i++) {
originalSeries.add(xData[i], yData[i]);
}
StringBuilder xList = new StringBuilder("x = [");
StringBuilder yList = new StringBuilder("y = [");
for (int i = 0; i < numPoints; i++) {
double tVal = tNew[i];
double xi = fx.value(tVal);
double yi = fy.value(tVal);
interpolatedSeries.add(xi, yi);
xList.append(String.format("%.2f", xi));
yList.append(String.format("%.2f", yi));
if (i != numPoints - 1) {
xList.append(", ");
yList.append(", ");
}
}
xList.append("]");
yList.append("]");
System.out.println(xList);
System.out.println(yList);
XYSeriesCollection dataset = new XYSeriesCollection();
dataset.addSeries(originalSeries);
dataset.addSeries(interpolatedSeries);
JFreeChart chart = ChartFactory.createXYLineChart(
"Interpolation Visualization",
"X",
"Y",
dataset,
PlotOrientation.VERTICAL,
true,
true,
false
);
JFrame frame = new JFrame("JFreeChart Example");
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.add(new ChartPanel(chart));
frame.pack();
frame.setLocationRelativeTo(null);
frame.setVisible(true);
}
}데이터를 다음과 같이 입력하였을 때
double[] xData = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
double[] yData = {2, 4, 7, 11, 9, 8, 12, 14, 17, 25};
실행을 해보면
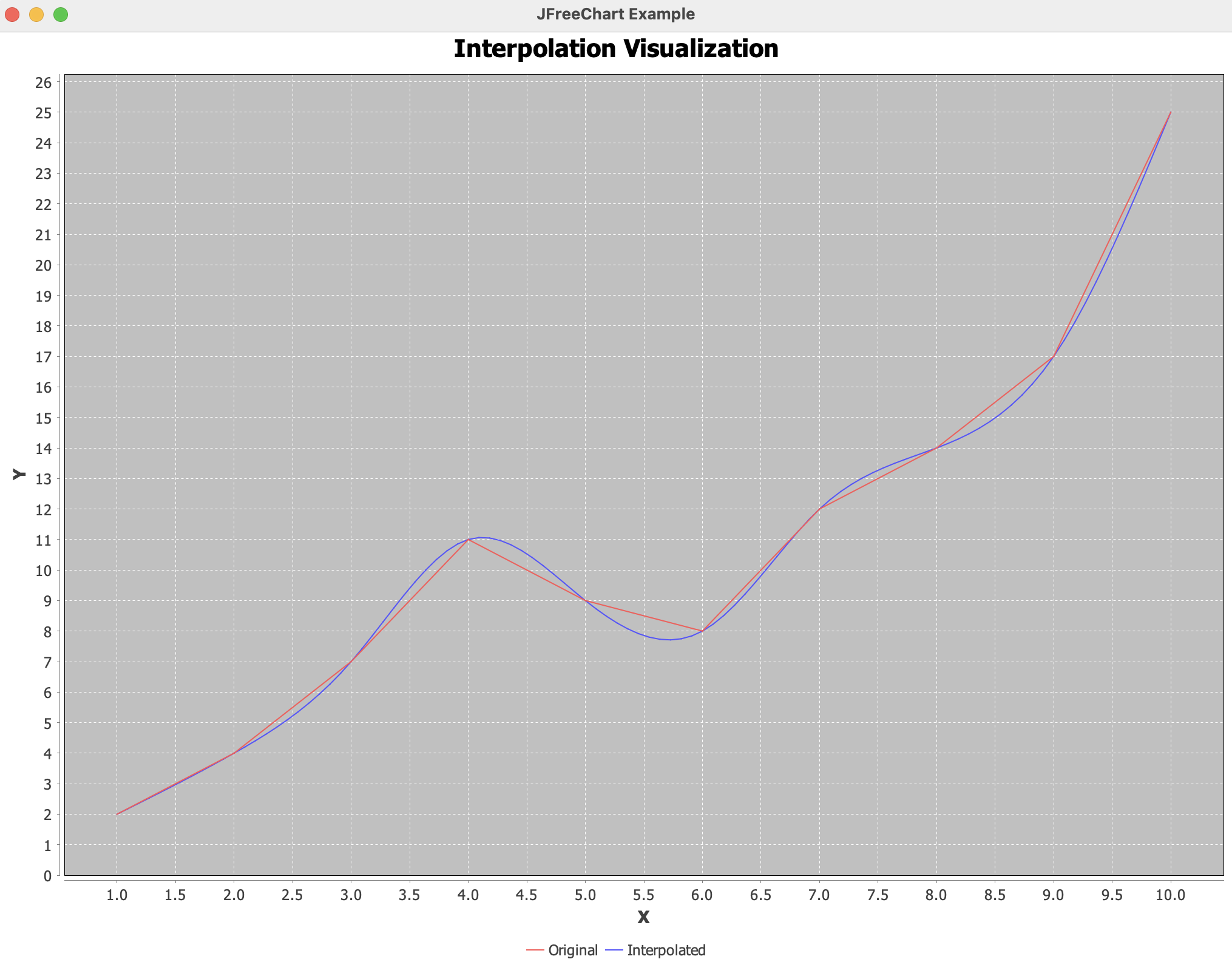
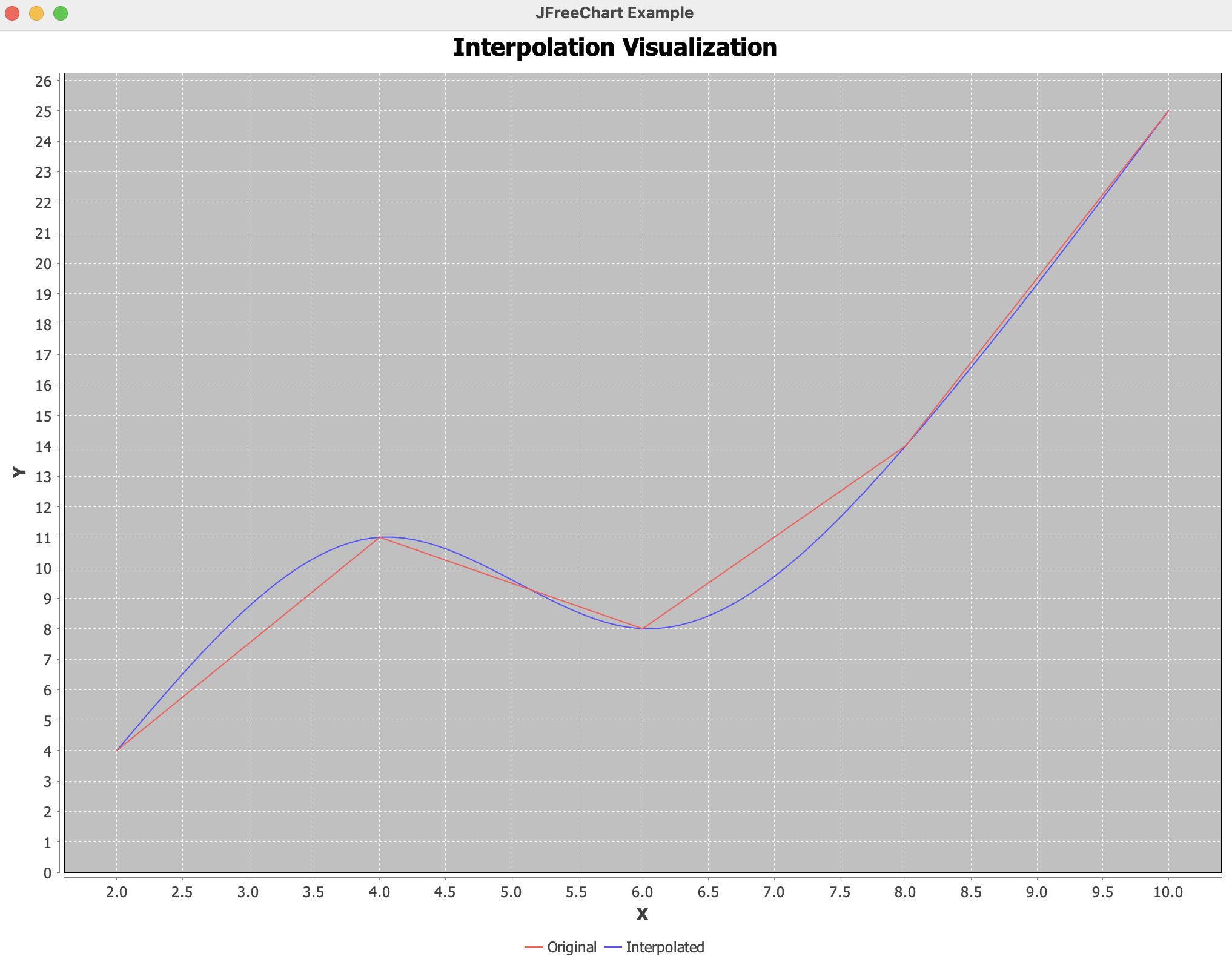
이런식으로 빨간색 데이터들에 대한 보간 값이 그래프 형태로 그려지게된다.
+ 홀수번째 인덱스의 값들만 지우고 다시 실행해보면
double[] xData = {2, 4, 6, 8, 10};
double[] yData = {4, 11, 8, 14, 25};
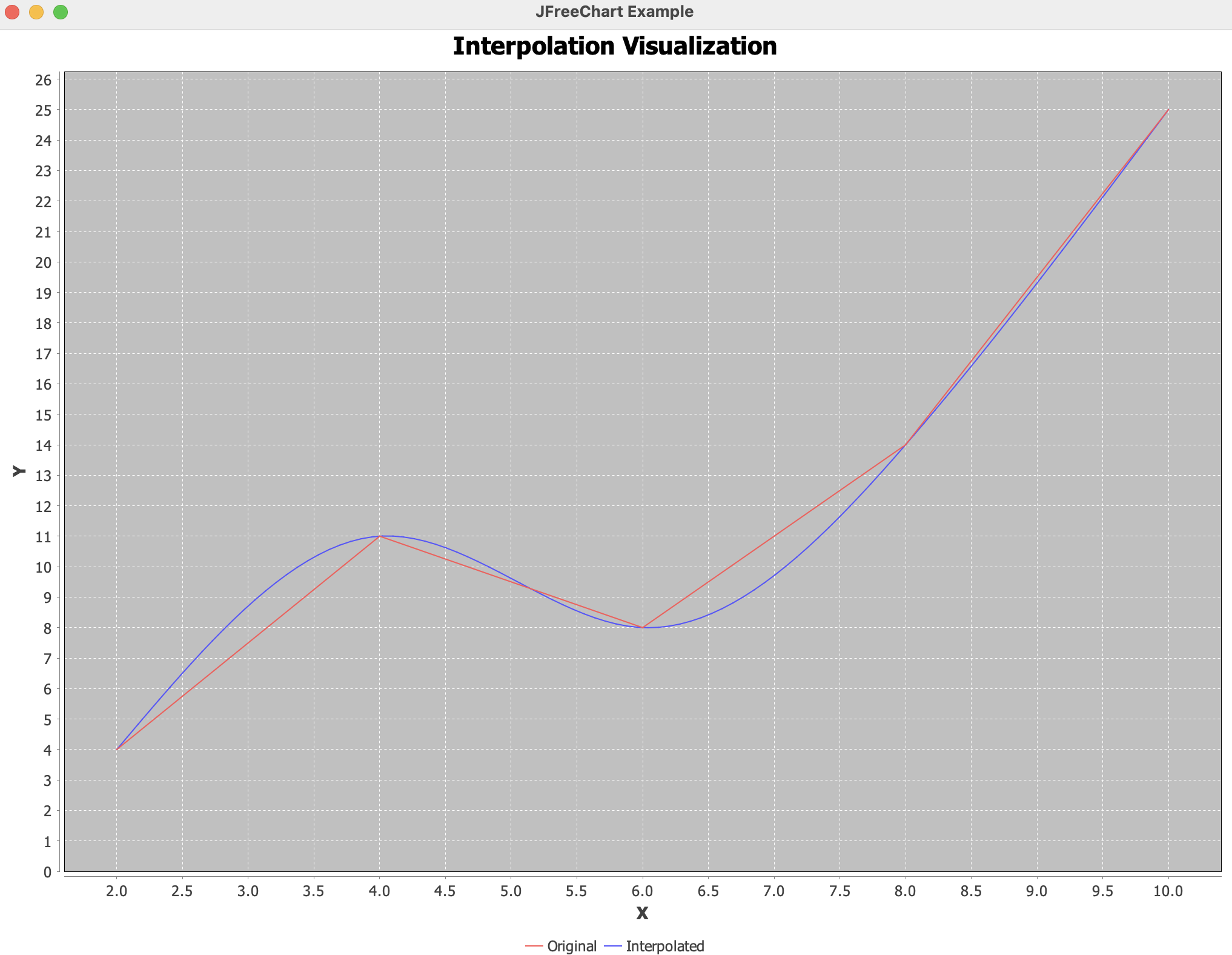
이처럼 유사하지만 단순한 그래프가 보여진다.
보간은 단순한 수학 개념이지만, 실제 데이터 시각화나 머신러닝 전처리 과정 등 다양한 분야에서 매우 유용하게 사용된다.
자바에서도 적절한 라이브러리를 활용하면 직관적이고 깔끔한 보간 구현 및 시각화가 가능하다.
