알고리즘의 성능분석
수행시간 측정 코드(c언어)
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main() {
clock_t start, finish;
double duration;
start = clock(); //측정시작
/*
측정하고자 하는 코드 입력
*/
finish = clock(); //측정종료
duration = (double)(finish - start) / CLOCKS_PER_SEC;
printf("해당 코드의 수행 시간은 %f초 입니다.\n", duration);
return 0;
}
step count
코드의 연산횟수는 각 단계별 횟수를 구한 다음 모두 합쳐 총값을 구하면 된다.
for (i = 0; i < n; i++)
for ( j =1; j < n; j *= 2)
print("Hello");위의 코드와 같이 중첩문의 스텝 카운트를 구한다면
첫 번째 반복문에서의 연산 횟수 n번
두 번째 반복문에서의 연산 횟수 log₂n번
따라서 총 연산 횟수는 n * log₂n = nlog₂n이 되는 것을 알 수 있다.
두 번째 반복문 연산 횟수 구하는 방법 - 자세히 봐야할 부분은 j의 값이 두 배씩 늘어난다는 점이다. 그렇기 때문에 연산 횟수를 t번 이라고 가정했을 때 2^t가 n에 도달할 때까지 식을 반복하게 되는 것이다. 이를 식으로 푼다면 t = log₂n이 되는 것이다.
복잡도 계산은 많이 연습하는게 답이 것 같아서 연습문제 사이트 첨부..
빅오표기법(big-O notation)
빅오표기법이란 점근표기법으로 알고리즘의 효율성을 알려주는 시간복잡도를 나타내기 위해 사용한다.
위에서 알고리즘의 시간복잡도가 연산횟수를 의미하는 것임을 말했는데 이 말은 즉, 입력값 n이 커짐에 따라 복잡도가 증가하게 된다는 것이다. 이때 빅오표기법은 상한을 알려주는 표기법으로 가장 늦게 실행되었을 경우를 알려주는 것이다.
빅오표기법의 특징은 다음과 같다
- 상수항의 무시
- 최고차항만 표기
- 계수 무시
예를 들어 복잡도 3n³+n+25 를 가지고 있다고 한다면 빅오표기법으로는 O(n³)가 된다는 것이다. 위의 코드의 스텝 카운트에서 나온 nlog₂n 의 값도 빅오표기법으로 나타낸다면 O(nlogn)이 된다.
빅오표기법의 수학적 정의
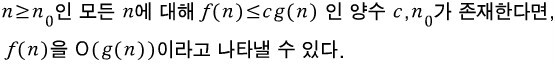
저기서 c는 양의 상수를 뜻한다. 즉 위의 조건을 만족하는 양의 상수가 존재한다면 f(n) = O(g(n)은 성립한다는 것이다.
예를 들어 3n+2는 3n+2 ≤ cn 을 만족시키는 양의 상수 c가 존재하기 때문에 에 3n+2 = O(n)이 성립될 수 있는 것이다. 차수가 달라도 마찬가지다.
10n²+4n+2 도 10n²+4n+2 ≤ cn² 을 만족시키기 때문에 10n²+4n+2 = O(n²) 이 성립될 수 있다.
실행속도 비교
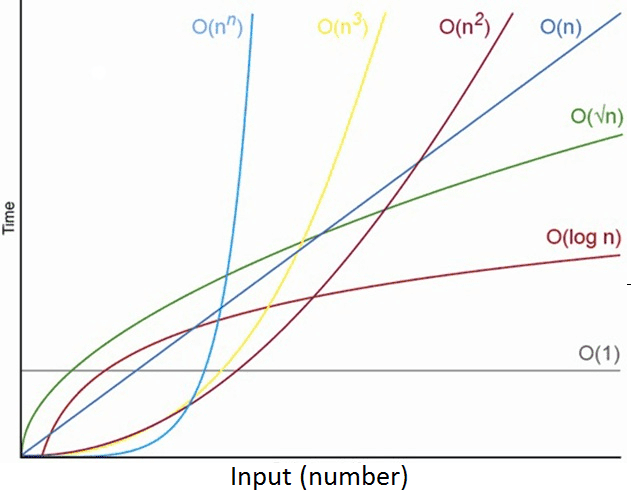
O(1) < O(logn)< O(n) < O(nlogn) < O(n²) < O(2ⁿ) < O(n!)
여기서 O(1)은 상수항을 의미하며 입력값에 상관없이 실행시간이 동일한 알고리즘을 뜻한다.
위의 빅오표기법을 그래프로 표시하면 다음과 같다.
빅오표기법 외
-
빅오메가(Big-Ω(Big-Omega)) - 빅오와는 반대로 하한을 나타내는 표기법으로 가장 최선의 시간을 알려준다.
-
빅세타(Big-θ(Big-Theta)) - 빅오 + 빅오메가를 모두 만족하는 경우를 나타내는 표기법이다.
여러가지 표기법들이 있지만 보통 알고리즘의 시간복잡도가 항상 최선의 경우를 가지지 못하기 때문에 상한을 나타내는 빅오표기법을 가장 많이 쓴다.
여기서 또 주의해야하는 것은 세가지 표기법 모두 점근법이기 때문에 정확한 값이 아닌 대략적인 값을 보여주는 것임을 알아야한다.
끝-!
[참고 자료]
교재: C언어로 쉽게 풀어쓴 자료구조
