[백준] 1707 - 이분 그래프 (JAVA)

백준 1707 - 이분그래프

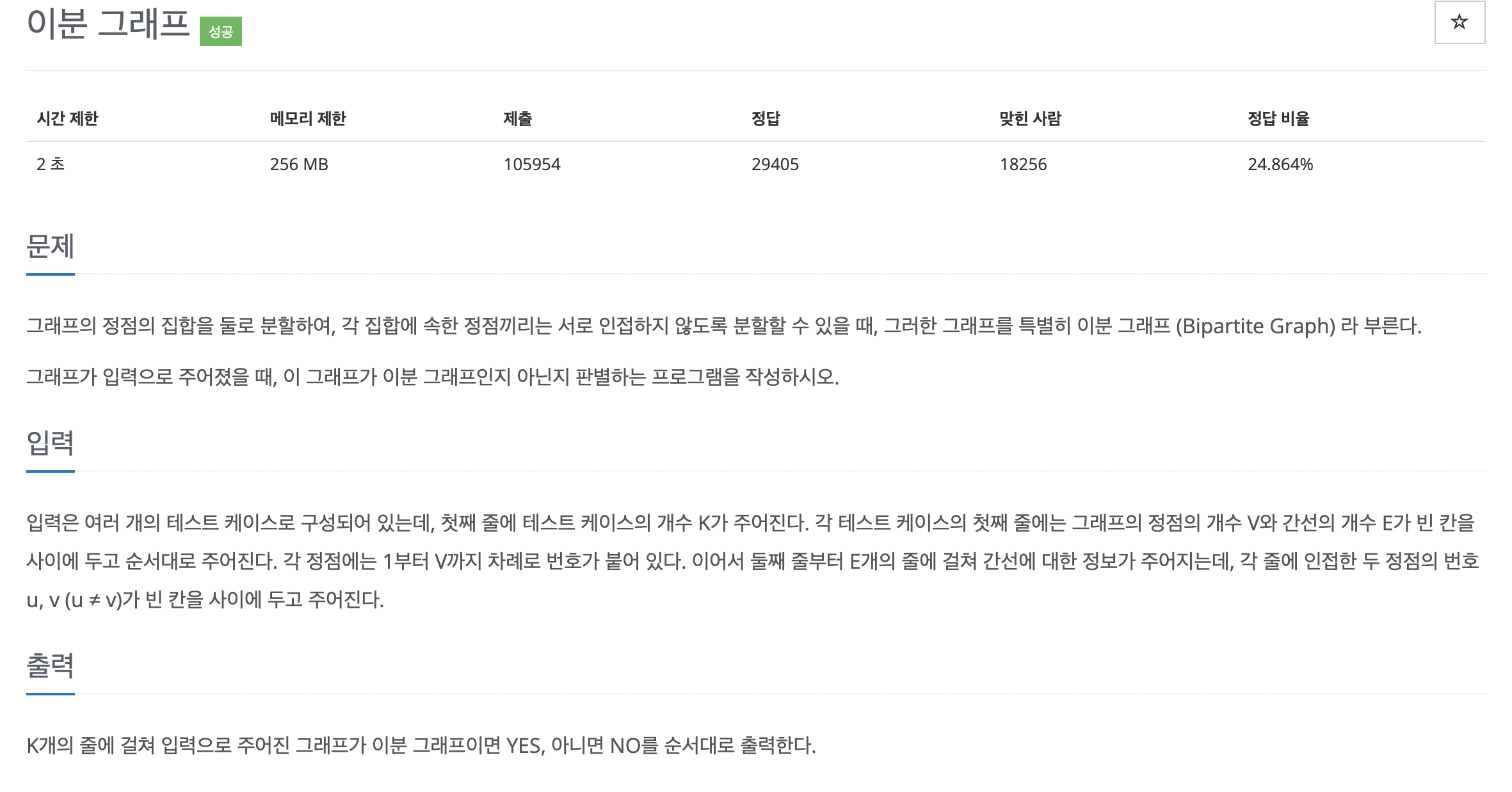
처음에는 '이분 그래프'라는 개념을 처음 접해봐서 이분 그래프 개념 자체를 이해하는 데 애먹었다. 친절한 챗GPT의 도움을 받아 이해가 안되는 걸 물어가며 차근차근 이해했다. 그러고나서 정점을 서로 다른 그룹에 나누는 아이디어까지는 생각보다 쉽게 떠올렸는데 자꾸 시간초과가 났다.
boolean으로 된 visited 배열과 각각의 정점을 다른 그룹에 담을 List 배열까지 만들었더니 이게 시간을 많이 잡아먹었었던 것 같다.
visited 배열을 boolean이 아니라 int 배열로 선언하고 1 혹은 -1로 그룹을 나누어서 구현했더니 통과했다!

그리고 나는 단순히 1부터 V까지 정점이 있으니까 bfs든 dfs든 1부터 시작해서 순회하면 되겠지~ 생각했는데 중간에 자꾸 틀렸다고 나오더라... 그래서 정점들을 전부 순회하는 for문 안에서 bfs와 dfs를 돌도록 수정했더니 통과할 수 있었다.
중간에 연결되지 않은 정점과 간선도 있다는 것 명심!! 나만 하는 실수인가?

아래는 bfs와 dfs로 구현한 전체 코드이다. 메모리와 시간은 둘 다 비슷하게 소요된다. (dfs가 아주 근소한 차이로 빠르긴하다.)

import java.io.*;
import java.util.*;

// 1707 - 이분 그래프(Bipartite Graph)
public class Main {
    static int[] visited;
    static boolean isBipartite;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;
        int K = Integer.parseInt(br.readLine());
        for (int i = 0; i < K; i++) {
            isBipartite = true;
            st = new StringTokenizer(br.readLine());
            int V = Integer.parseInt(st.nextToken()); // 정점
            int E = Integer.parseInt(st.nextToken()); // 간선
            List<List<Integer>> vertexes = new ArrayList<>();
            for (int j = 0; j < V + 1; j++) {
                vertexes.add(new ArrayList<>());
            }
            for (int j = 0; j < E; j++) {
                st = new StringTokenizer(br.readLine());
                int u = Integer.parseInt(st.nextToken());
                int v = Integer.parseInt(st.nextToken());

                vertexes.get(u).add(v);
                vertexes.get(v).add(u);
            }
            bw.write(isBipartiteGraph(vertexes) ? "YES" : "NO");
            bw.write("\n");
        }

        bw.flush();
        bw.close();
    }

    static boolean isBipartiteGraph(List<List<Integer>> graph) {
        visited = new int[graph.size()];
        boolean result = false;
//        return bfs(graph);
  // bfs로 풀 때는 아래를 주석처리하면 된다
        for (int i = 1; i < graph.size(); i++) {
            if (visited[i] == 0) {
                visited[i] = 1;
                result = dfs(graph, i);
                if(!result){
                    return result;
                }
            }
        }

        return result; 
    }


    static boolean bfs(List<List<Integer>> graph) {
        Queue<Integer> queue = new LinkedList<>();

        for (int k = 1; k < graph.size(); k++) {
            if (visited[k] == 0) {
                queue.add(k);
                visited[k] = 1;
            }
            while (!queue.isEmpty()) {
                int vertex = queue.poll();
                int currentGroup = visited[vertex];
                int oppositeGroupIndex = currentGroup * -1;

                for (int i : graph.get(vertex)) {
                    if (visited[i] != 0) {
                        // i들이 같은 그룹에 없어야함! 같은 그룹에 있는지 확인
                        if (visited[i] == currentGroup) {
                            return false;
                        }
                    } else {
                        // 다른 그룹에 넣어야함!
                        visited[i] = oppositeGroupIndex;
                        queue.add(i);
                    }
                }
            }
        }

        return true;
    }


    static boolean dfs(List<List<Integer>> graph, int index) {
        int currentGroup = visited[index];
        int opposite = currentGroup * -1;

        for (int v : graph.get(index)) {
            if (visited[v] != 0) {
                if (visited[v] == currentGroup) {
                    return false;
                }
            } else {
                visited[v] = opposite;
                if (!dfs(graph, v)) {
                    return false;
                }
            }
        }
        return true;
    }
}